1mol of a mono-atomic gas is subjected to following cyclic process:
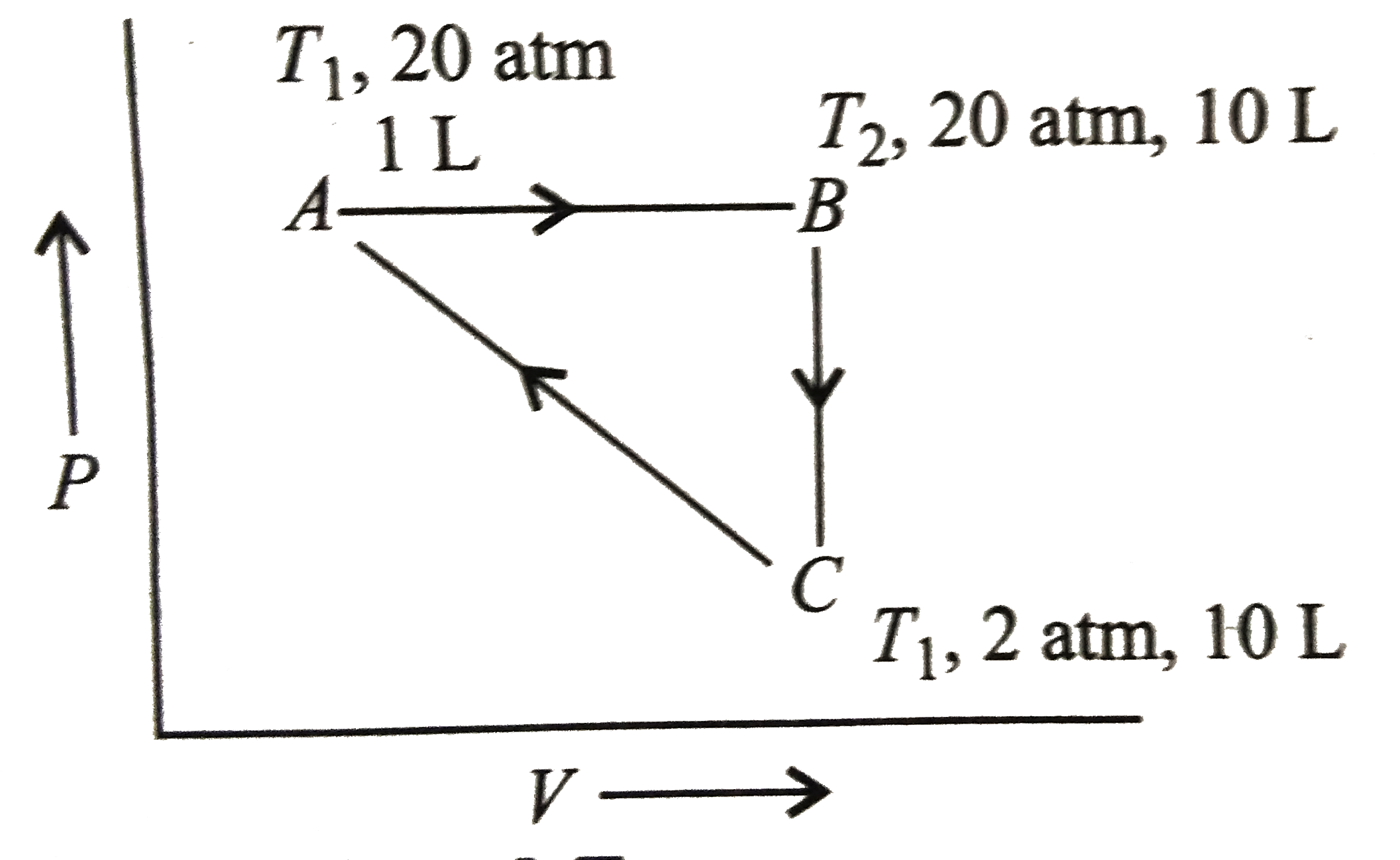
a. Calculate T1 and T2.
a. At A: (Using ideal gas equation)
pV=nRT
20×1=1×0.082×T1
T1=243.6K
At B: PV=nRT
20×10=1×0.0820×T2
T2=2436.05K
b. Path AB: Isobaric process (ΔU=0,q=W)
W=PΔV=20×9=180Latm=108×101.34.185cal
=4356.9cal
(work in compression is positive)
Path BC: Isochoric process
W=0
qv=ΔU=nCvΔT=1×32R×(2436−243.6)
=32×2×2192.4=6577.2cal
It is cooling process: qv=−6577.2cal
Path CA: It is an isothermal compression ΔU=0
q=w=2.303nRTlog.V2V1
=2.303×1×2×log.101=1122.02cal
Topper's Solved these Questions
- THERMODYNAMICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Exercise
1 Videos
- THERMODYNAMICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Ex 6.1
26 Videos
- STOICHIOMETRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STOICHIOMETRYEXERCISE - Archives Subjective
33 Videos
Similar Questions
Calculate T1&T2.
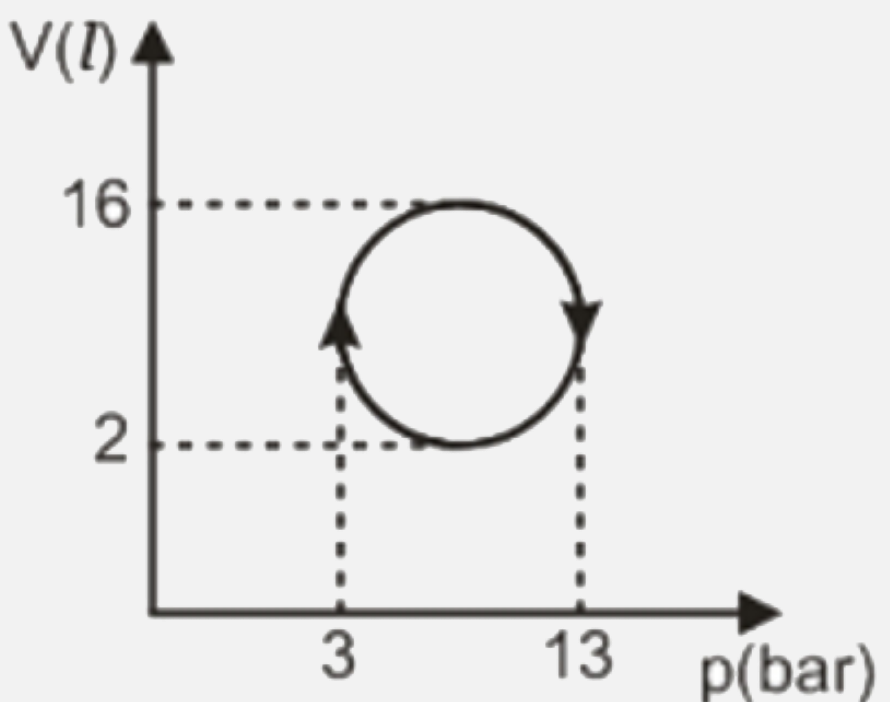
View SolutionWork done (in kJ) by the gas in the following cyclic process is
View SolutionOne mole of an ideal mono-atomic gas is taken round cyclic process ABCD as shown in figure below. Calculate work done by the gas.
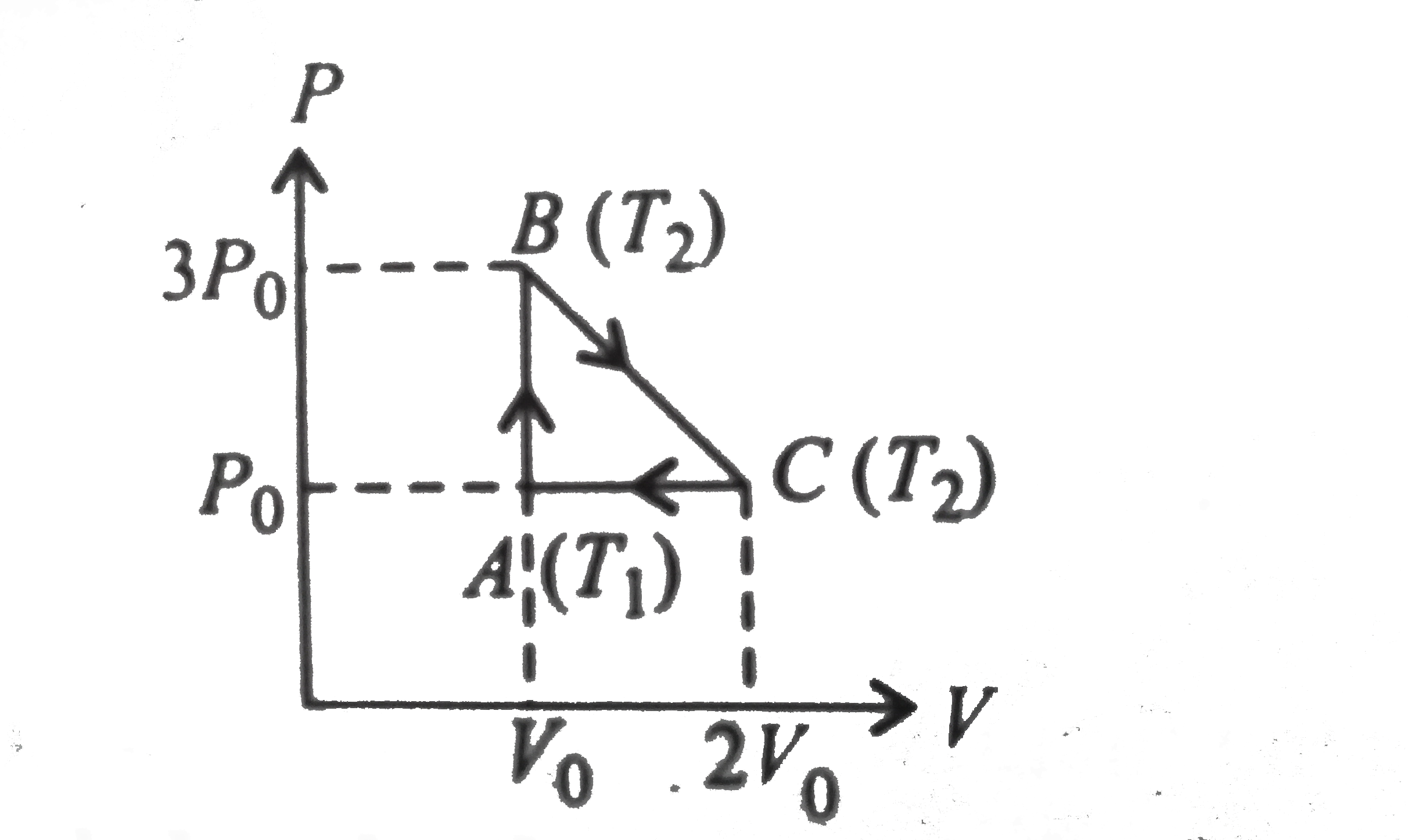
View SolutionOne mole of an ideal mono-atomic gas is taken round cyclic process ABC as shown in figure below. Calculate work done
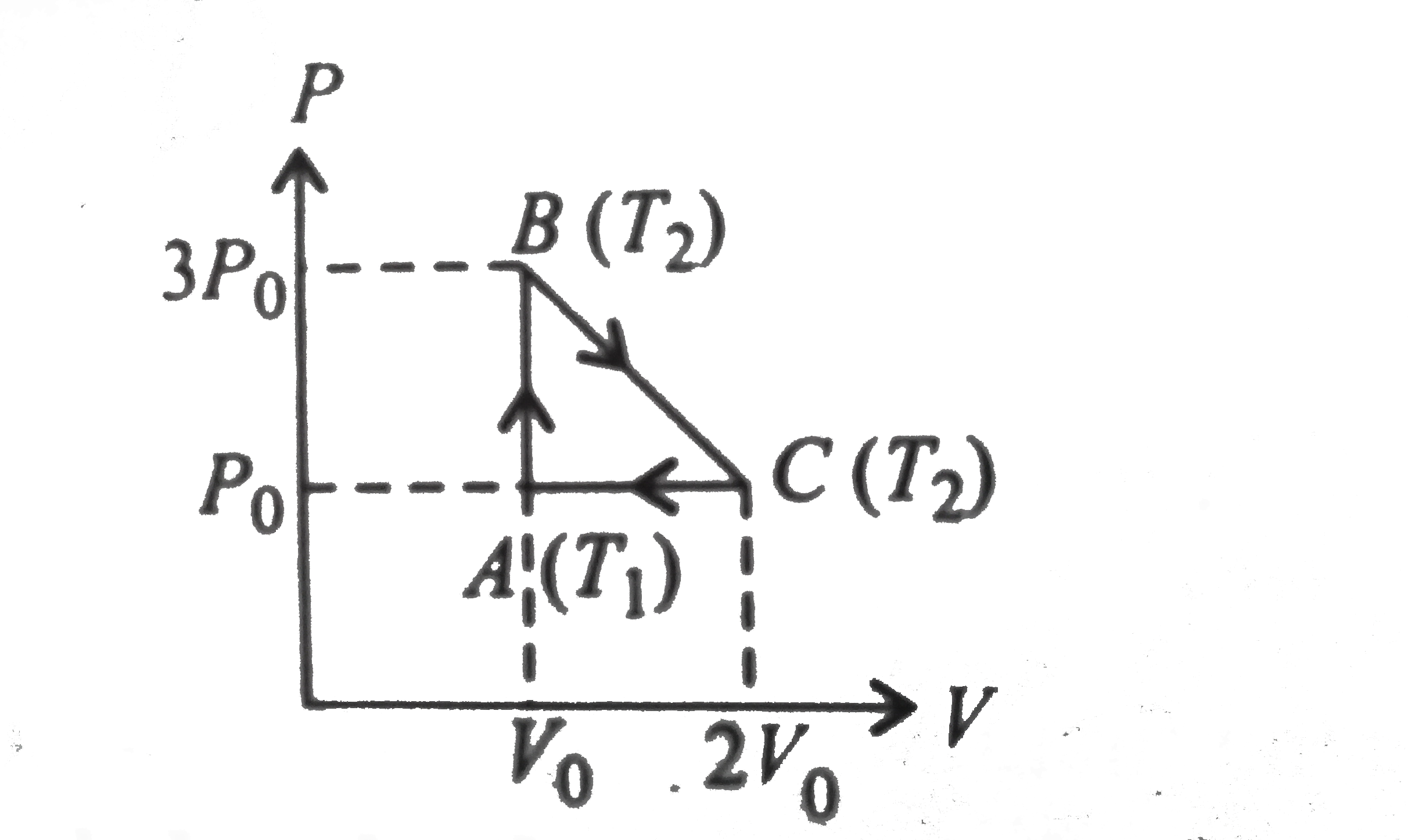
View SolutionOne mole of an ideal mono-atomic gas is taken round cyclic process ABC as shown in figure below. Calculate work done
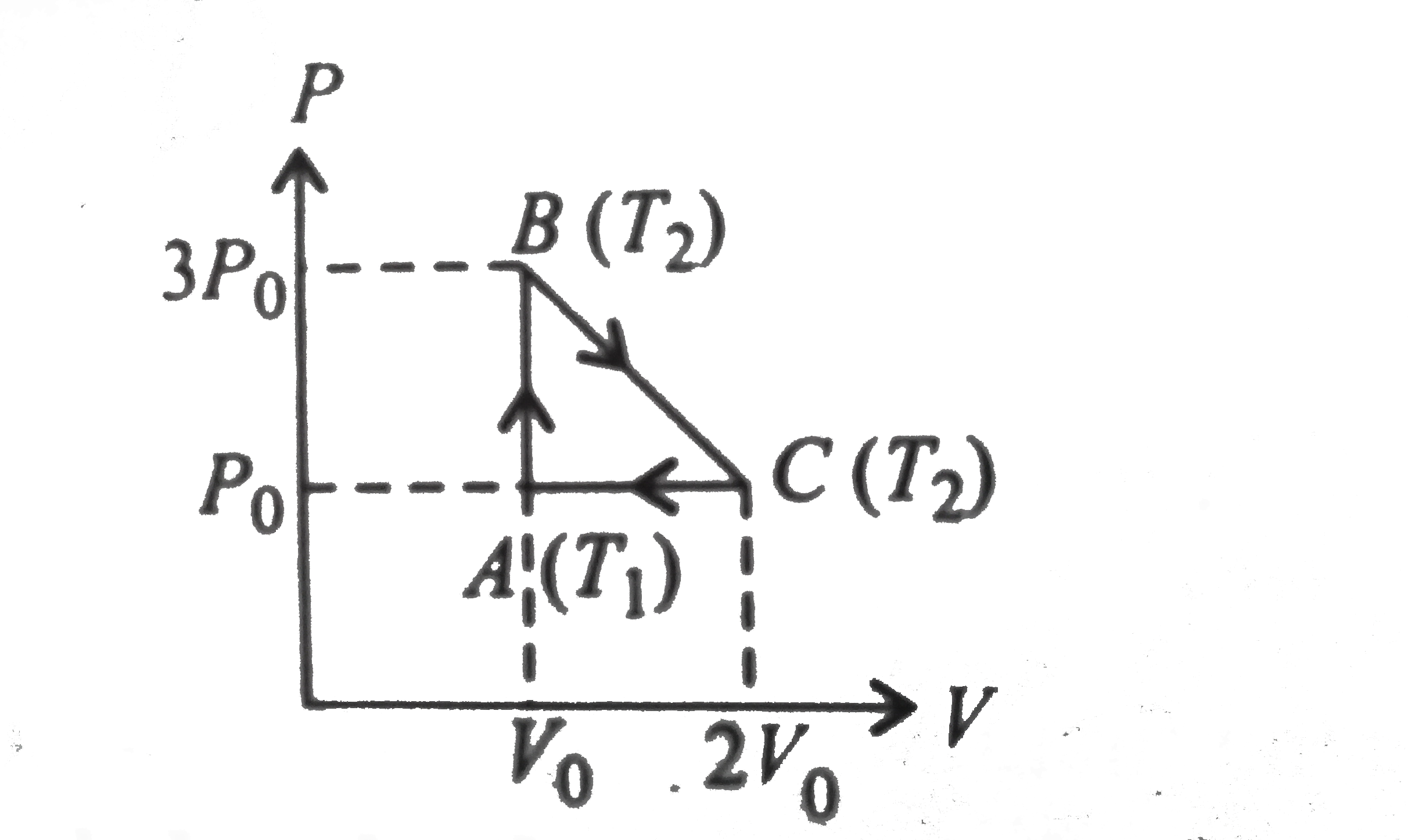
View SolutionA sample of mono-atomic ideal gas is taken through a cyclic process ABCDA. A graph is plotted in which heat exchanged by the gas upto an instant is shown on x-axis and work done by the gas upto that instant is shown on y-axis.
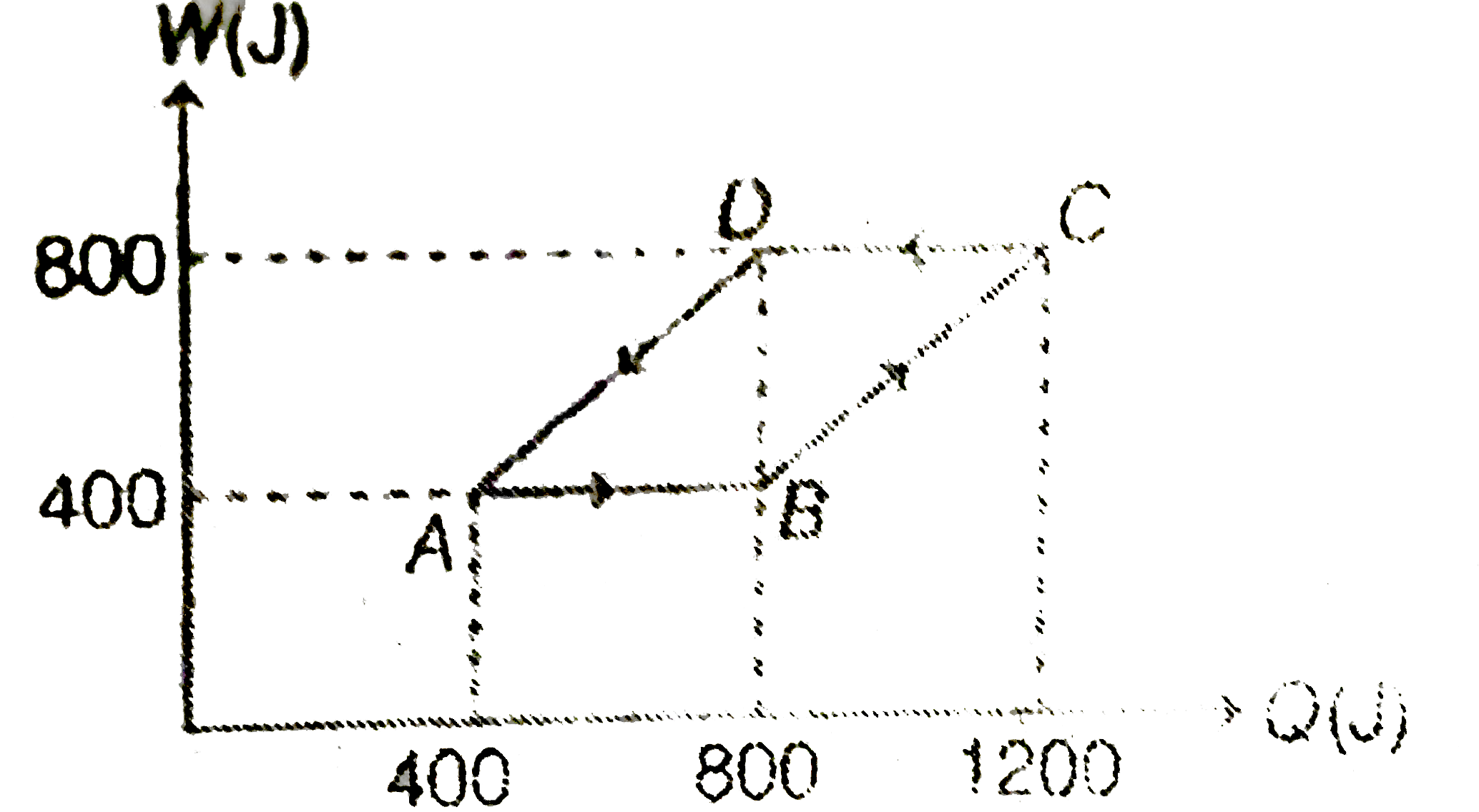
The given cyclic process can be represented on a pressure-volume graph as:
View Solutionn moles of a diatomic gas has undergone a cyclic process ABC as shown in figure. Temperature at a is T0. Find volume at C
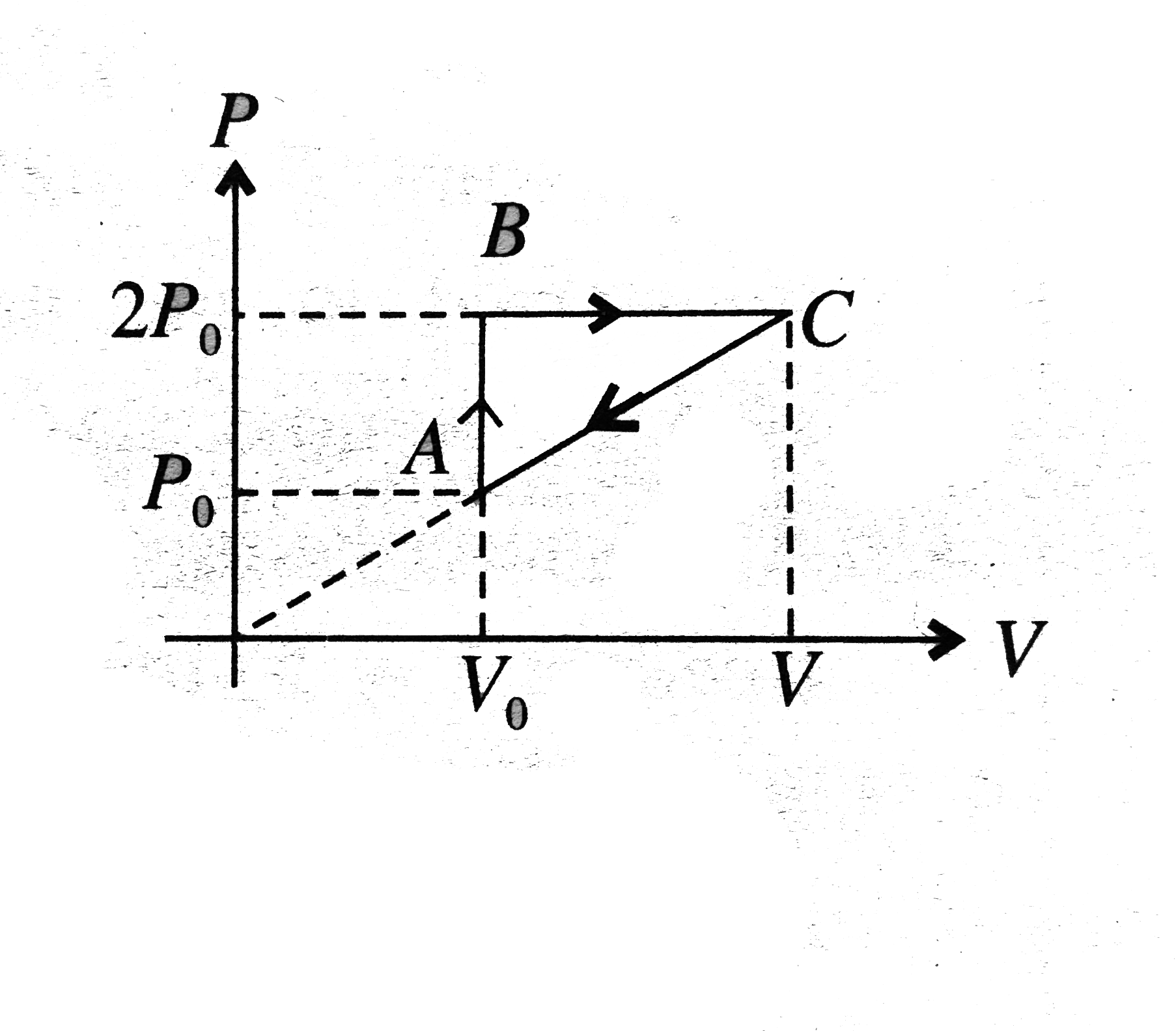
View SolutionTwo moles of an ideal mono-atomic gas undergo a cyclic process as shown in the figure. The temperatures in different states are given as 6T1=3T2=2T4=T3=1800K. Determine the work done by the gas during the cycle.
View Solution
Calculate a, T1,T2,T1'&T2'.
View SolutionTwo moles of monatomic ideal gas is taken through a cyclic process shown on P−T diagram in Fig. Process CA is represented as PT = constant. If efficiency of given cyclic process is
1−x121n2+15
then find x,

View Solution
