A sample of an ideal gas is expanded to twice its original volume of 1m3 in a reversible process for which P=αV2, where α=5atmm−6. If CV,m=20Jmol−1K−1, determine moalr change in entropy (ΔSm) for the process.
To determine the molar change in entropy (ΔSm) for the process where a sample of an ideal gas is expanded to twice its original volume in a reversible process, we can follow these steps:
Step 1: Understand the Process
We know that the gas is expanded from an initial volume V1=1m3 to a final volume V2=2m3. The pressure is given by the equation P=αV2, where α=5atmm−6.
Step 2: Use the First Law of Thermodynamics
According to the first law of thermodynamics:
dQ=dU+dW
Where:
- dQ is the heat added to the system,
- dU is the change in internal energy,
- dW is the work done by the system.
Step 3: Express dU and dW
For an ideal gas, the change in internal energy can be expressed as:
dU=nCV,mdT
Where CV,m=20Jmol−1K−1 is the molar heat capacity at constant volume.
The work done by the gas during expansion is given by:
dW=PdV
Substituting P from the given equation:
dW=αV2dV
Step 4: Substitute dW in the First Law Equation
Now, we can write:
dQ=nCV,mdT+αV2dV
Step 5: Relate dV to dT
Using the ideal gas law PV=nRT, we can express dV in terms of dT:
P=αV2⟹αV3=nRT⟹dT=R3αV2dV
Step 6: Substitute dT into the Equation for dQ
Substituting dT into the equation for dQ:
dQ=nCV,m(R3αV2dV)+αV2dV
This simplifies to:
dQ=(nCV,mR3αV2+αV2)dV
Step 7: Calculate the Change in Entropy
The change in entropy is given by:
ΔS=∫T2T1dQT
Substituting for dQ:
ΔS=∫T2T1(nCV,mR3αV2+αV2)dVT
Step 8: Find the Temperature Ratio
Using the ideal gas law:
T1=αV31R,T2=αV32R
Since V2=2V1:
T2T1=(2V1)3V31=8
Step 9: Substitute Values and Calculate ΔS
Now substituting the values:
ΔS=n(CV,mln(T2T1)+Rln(V2V1))
Since V2=2V1:
ΔS=n(CV,mln(8)+Rln(2))
Step 10: Final Calculation
Substituting CV,m=20Jmol−1K−1 and R=8.314Jmol−1K−1:
ΔS=1(20ln(8)+8.314ln(2))
Calculating the logarithms:
ΔS≈20×2.079+8.314×0.693
ΔS≈41.58+5.76≈47.34JK−1mol−1
Thus, the molar change in entropy (ΔSm) for the process is approximately:
ΔSm≈47.35JK−1mol−1
We know that the gas is expanded from an initial volume V1=1m3 to a final volume V2=2m3. The pressure is given by the equation P=αV2, where α=5atmm−6.
According to the first law of thermodynamics:
dQ=dU+dW
Where:
- dQ is the heat added to the system,
- dU is the change in internal energy,
- dW is the work done by the system.
For an ideal gas, the change in internal energy can be expressed as:
dU=nCV,mdT
Where CV,m=20Jmol−1K−1 is the molar heat capacity at constant volume.
dW=PdV
Substituting P from the given equation:
dW=αV2dV
Now, we can write:
dQ=nCV,mdT+αV2dV
Using the ideal gas law PV=nRT, we can express dV in terms of dT:
P=αV2⟹αV3=nRT⟹dT=R3αV2dV
Substituting dT into the equation for dQ:
dQ=nCV,m(R3αV2dV)+αV2dV
This simplifies to:
dQ=(nCV,mR3αV2+αV2)dV
The change in entropy is given by:
ΔS=∫T2T1dQT
Substituting for dQ:
ΔS=∫T2T1(nCV,mR3αV2+αV2)dVT
Using the ideal gas law:
T1=αV31R,T2=αV32R
Since V2=2V1:
T2T1=(2V1)3V31=8
Now substituting the values:
ΔS=n(CV,mln(T2T1)+Rln(V2V1))
Since V2=2V1:
ΔS=n(CV,mln(8)+Rln(2))
Substituting CV,m=20Jmol−1K−1 and R=8.314Jmol−1K−1:
ΔS=1(20ln(8)+8.314ln(2))
Calculating the logarithms:
ΔS≈20×2.079+8.314×0.693
ΔS≈41.58+5.76≈47.34JK−1mol−1
ΔSm≈47.35JK−1mol−1
Topper's Solved these Questions
- THERMODYNAMICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Exercise
1 Videos
- THERMODYNAMICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Ex 6.1
26 Videos
- STOICHIOMETRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STOICHIOMETRYEXERCISE - Archives Subjective
33 Videos
Similar Questions
A sample of ideal gas is expanded to twice its original volume of 1.00m3 in a quasi-static process for which p=αV2, with α=5.00atm/m6, as shown in Fig. How much work is done by the expanding gas?
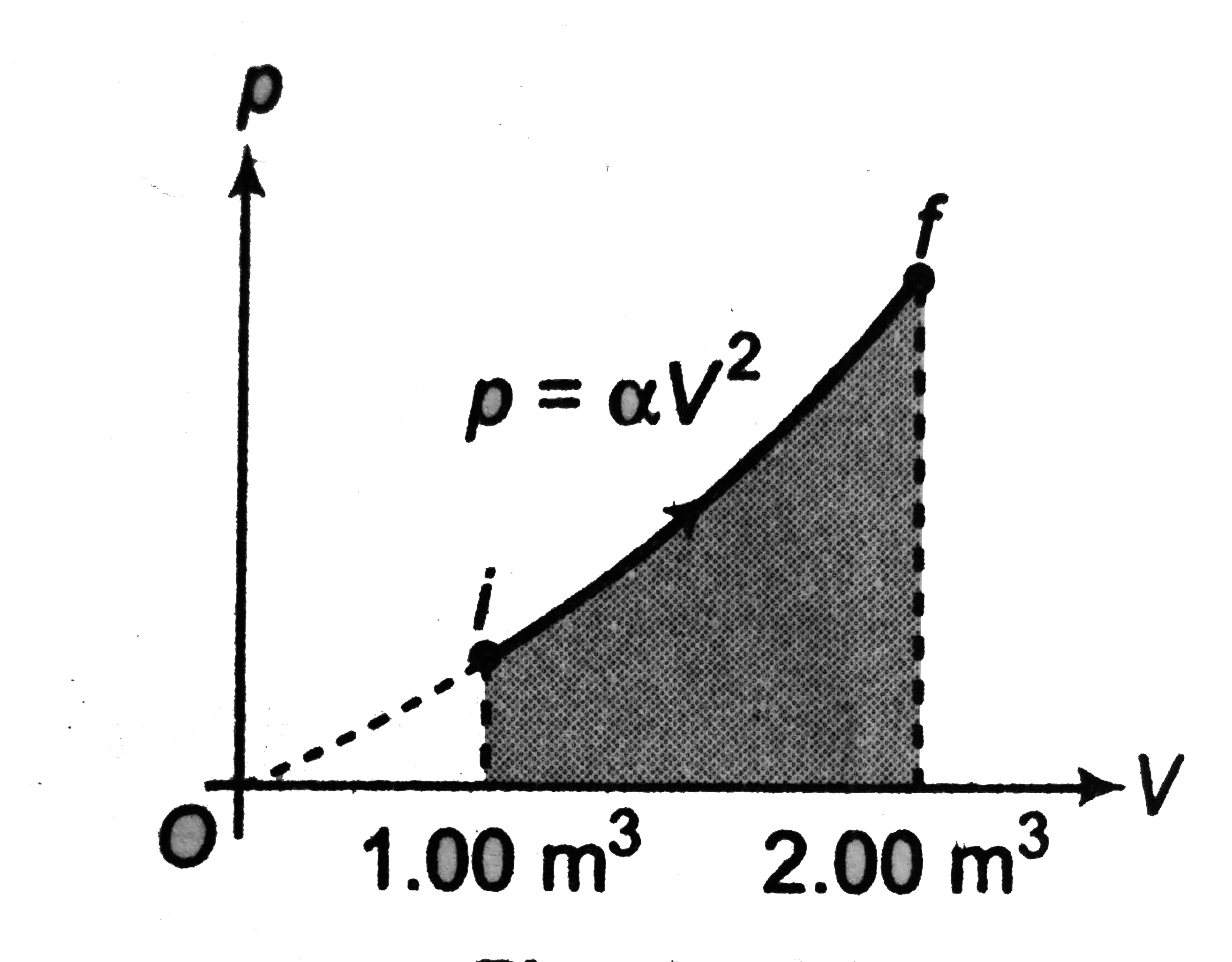
View SolutionA sample of ideal gas is expanded to twice its original volume of 1.00m3 in a quasi-static process for which p=αV2, with α=5.00atm/m6, as shown in Fig. How much work is done by the expanding gas?

View SolutionA sample of an ideal gas is expanded 1m3 to 3m3 in a reversible process for which P=KV2 , with K=6bar/m6. What is work done by the gas (in kJ) ?
View SolutionA sample of an ideal gas is expanded from 1dm3 to 3 in a reversible process for which P=KV3, with K=1/5(atm/dm3), what is work done by gas (Latm)
View SolutionOne mole of an ideal gas at 300K is expanded isothermally from an inital volume of 1 litre to 10 litres. The ΔE for this process is (R=2calmol−1K−1)
View SolutionOne mole of an ideal gas at 27∘C expanded isothermally from an initial volume of 1 litre to 10 litre. The ΔU for this process is : (R=2calK−1mol−1)
View SolutionOne mole of an ideal gas at 250 K is expanded isothermally from an initial volume of 5 litre to 10 litres. The ΔE for this process is (R=2cal.Mol−1K−1)
View Solution5 mol of an ideal gas expand reversibly from a volume of 8dm3 to 80dm3 at an temperature of 27∘C. Calculate the change in entropy.
View SolutionWhen 5 moles of an ideal gas is expended at 350 K reversibly from 5 L to 40 L, then the entropy change for the process is (R = 2 cal mol−1K−1)
View SolutionTwo moles of an ideal gas at 1 atm are compressed to 2 atm at 273 K. The enthalpy change for the process is
View Solution
