1mol of an ideal gas undergoes reversible isothermal expansion form an initial volume V1 to a final volume 10V1 and does 10kJ of work. The initial pressure was 1×107Pa.
c. Calculate V2.
b. If there were 2mol of gas, what must its temperature have been?
To solve the given problem step by step, we will break it down into two parts: calculating V2 and finding the temperature when there are 2 moles of gas.
Part A: Calculate V2
1. Understand the Work Done in Isothermal Expansion:
The work done W during the isothermal expansion of an ideal gas can be expressed as:
W=−nRTln(V2V1)
Given that W=−10kJ=−10×103J, n=1mol, and V2=10V1, we can substitute these values into the equation.
2. Rearranging the Equation:
Since V2=10V1, we can rewrite the equation as:
−10×103=−2.303×n×R×Tln(10)
where R=8.314J/(mol K).
3. Calculate Temperature T:
Rearranging the equation to solve for T:
T=−10×103−2.303×1×8.314×ln(10)
Calculating T:
T=10×1032.303×8.314×2.3026≈522.23K
4. Calculate Pressure P2:
Using the ideal gas law, we can find P2:
P1V1=P2V2
Given P1=1×107Pa and V2=10V1:
P2=P1V1V2=1×107×V110V1=1×106Pa
5. Use Ideal Gas Law to Find V2:
Now, using the ideal gas equation:
P2V2=nRT
Substituting the known values:
1×106⋅V2=1⋅8.314⋅522.23
Solving for V2:
V2=1⋅8.314⋅522.231×106≈4.34×10−4m3
Part B: Calculate Temperature for 2 Moles
1. Use the Work Done Expression:
For 2 moles of gas, the work done remains the same:
W=−2.303nRTln(V2V1)
Substituting n=2:
−10×103=−2.303×2×8.314×Tln(10)
2. Rearranging the Equation for Temperature T:
Rearranging gives:
T=−10×103−2.303×2×8.314×ln(10)
Calculating T:
T=10×1032.303×2×8.314×2.3026≈261.3K
Final Answers:
- V2≈4.34×10−4m3
- Temperature for 2 moles of gas T≈261.3K
The work done W during the isothermal expansion of an ideal gas can be expressed as:
W=−nRTln(V2V1)
Given that W=−10kJ=−10×103J, n=1mol, and V2=10V1, we can substitute these values into the equation.
Since V2=10V1, we can rewrite the equation as:
−10×103=−2.303×n×R×Tln(10)
where R=8.314J/(mol K).
Rearranging the equation to solve for T:
T=−10×103−2.303×1×8.314×ln(10)
Calculating T:
T=10×1032.303×8.314×2.3026≈522.23K
Using the ideal gas law, we can find P2:
P1V1=P2V2
Given P1=1×107Pa and V2=10V1:
P2=P1V1V2=1×107×V110V1=1×106Pa
Now, using the ideal gas equation:
P2V2=nRT
Substituting the known values:
1×106⋅V2=1⋅8.314⋅522.23
Solving for V2:
V2=1⋅8.314⋅522.231×106≈4.34×10−4m3
For 2 moles of gas, the work done remains the same:
W=−2.303nRTln(V2V1)
Substituting n=2:
−10×103=−2.303×2×8.314×Tln(10)
Rearranging gives:
T=−10×103−2.303×2×8.314×ln(10)
Calculating T:
T=10×1032.303×2×8.314×2.3026≈261.3K
- V2≈4.34×10−4m3
- Temperature for 2 moles of gas T≈261.3K
Topper's Solved these Questions
- THERMODYNAMICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Ex 6.2
27 Videos
- THERMODYNAMICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Ex 6.3
27 Videos
- THERMODYNAMICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Exercise
1 Video
- STOICHIOMETRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - STOICHIOMETRYEXERCISE - Archives Subjective
33 Videos
Similar Questions
Knowledge Check
The work done, W, during an isothermal process in which the gas expands from an intial volume V1, to a final volume V2 is given by (R : gas constant, T : temperature )
AR(V2−V1)logeT1T2BR(T2−T1)loge(V1V2)CRTloge[V2V1]D2RTloge[V1V2]
A sample of ideal gas undergoes isothermal expansion in a reversible manner from volume V1 to volume V2. The initial pressure is P1 and the final pressure is P2. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume V1→V2. The initial pressure being same but final pressure is P3.
The work of expansion in adiabatic process (wadi) is related to work of expansion in isothermal process (wiso) is
View SolutionA sample of ideal gas undergoes isothermal expansion in a reversible manner from volume V1 to volume V2. The initial pressure is P1 and the final pressure is P2. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume V1→V2. The initial pressure being same but final pressure is P3.
Which relation is correct (γ=CPCV)?
View SolutionA sample of ideal gas undergoes isothermal expansion in a reversible manner from volume V1 to volume V2. The initial pressure is P1 and the final pressure is P2. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume V1→V2. The initial pressure being same but final pressure is P2.
If P3 and P2 are equal, then
View SolutionA sample of ideal gas undergoes isothermal expansion in a reversible manner from volume V1 to volume V2. The initial pressure is P1 and the final pressure is P2. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume V1→V2. The initial pressure being same but final pressure is P2.
Which graphic representation is correct
a.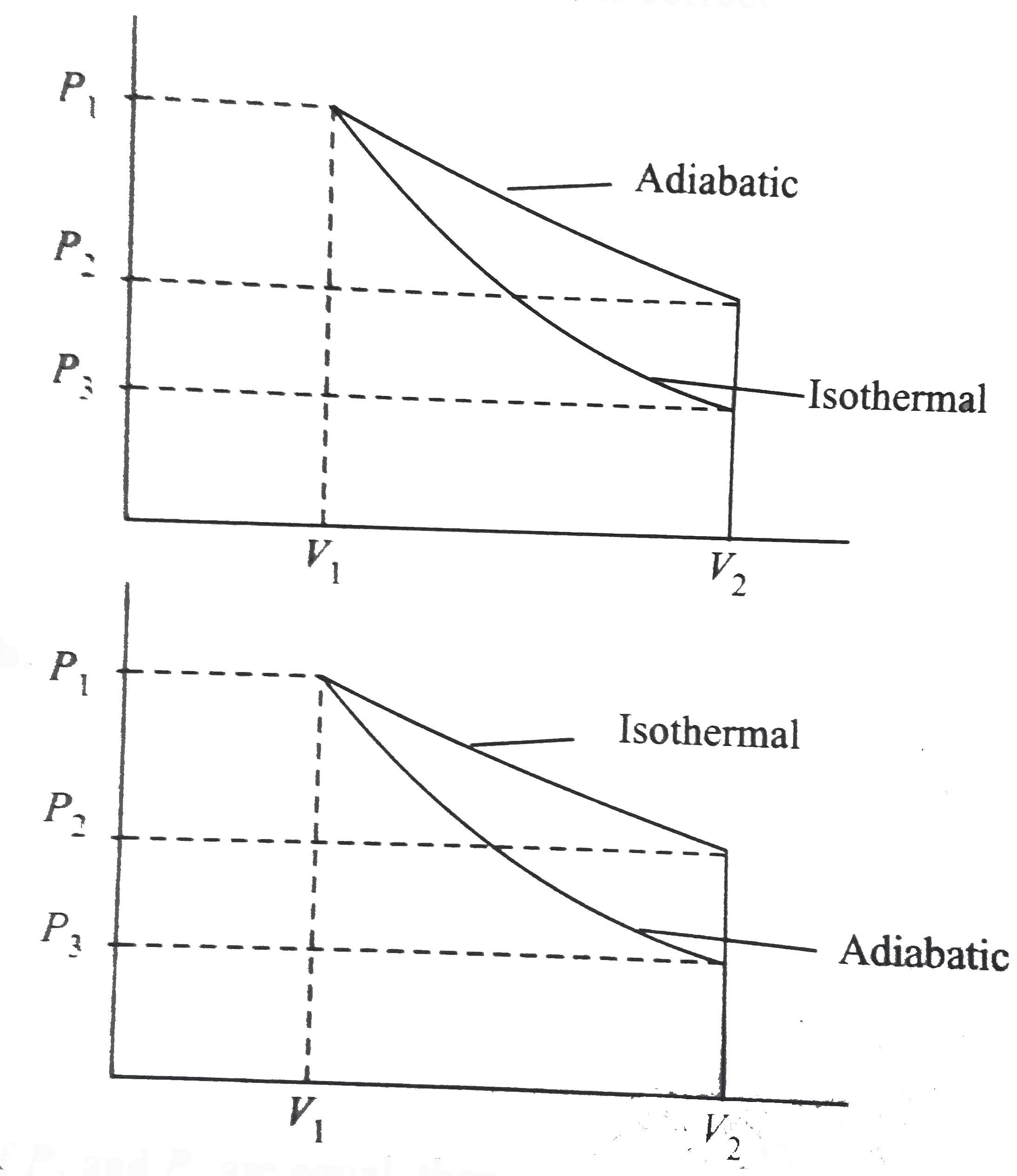
View SolutionA sample of ideal gas undergoes isothermal expansion in a reversible manner from volume V1 to volume V2. The initial pressure is P1 and the final pressure is P2. The same sample is then allowed to undergoes reversible expansion under adiabatic conditions from volume V1→V2. The initial pressure being same but final pressure is P3.
Which of the following is correct?
View Solution6mole of an ideal gas expand isothermally and reversibly from a volume of 1 litre to a volume of 10 litre at 27° C .The maximum work is done
View SolutionTwo moles of a gas expand reversibly and isothermally at temperature of 300K. Initial volume of the gas is 1 L while the final pressure is 4.926 atm . The work done by gas is
View Solution