The energy of activation for a reaction is 100KJmol−1. The peresence of a catalyst lowers the energy of activation by 75%. What will be the effect on the rate of reaction at 20∘C, other things being equal?
To solve the problem step by step, we will use the Arrhenius equation and analyze the effect of a catalyst on the rate of reaction.
Step 1: Understand the Arrhenius Equation
The Arrhenius equation is given by:
k=Ae−EaRT
where:
- k is the rate constant,
- A is the pre-exponential factor,
- Ea is the activation energy,
- R is the universal gas constant (8.314 J/mol·K),
- T is the temperature in Kelvin.
Step 2: Determine the Activation Energy Without Catalyst
The activation energy without the catalyst is given as:
Ea=100 kJ/mol=100,000 J/mol
Step 3: Calculate the Activation Energy With Catalyst
The catalyst lowers the activation energy by 75%. Therefore, the new activation energy (E′a) with the catalyst is:
E′a=Ea−0.75×Ea=100,000−0.75×100,000=25,000 J/mol
Step 4: Write the Rate Constants
- The rate constant without the catalyst (k1):
k1=Ae−100,000RT
- The rate constant with the catalyst (k2):
k2=Ae−25,000RT
Step 5: Calculate the Ratio of Rate Constants
To find the effect of the catalyst on the rate of reaction, we need the ratio k2k1:
k2k1=Ae−25,000RTAe−100,000RT=e−25,000RT+100,000RT=e75,000RT
Step 6: Substitute Values to Find the Ratio
Now, we substitute R=8.314 J/mol⋅K and T=20∘C=293 K:
k2k1=e75,0008.314×293
Calculating the exponent:
75,0008.314×293≈75.0
Thus,
k2k1=e75.0
Step 7: Calculate the Rate Ratio
The ratio of the rates of reaction (R2R1) is equal to the ratio of the rate constants:
R2R1=k2k1=e75.0
This indicates that the rate of reaction in the presence of the catalyst is significantly higher than in its absence.
Conclusion
The presence of the catalyst increases the rate of reaction by a factor of e75.0, which is a very large number, indicating a dramatic increase in the rate of reaction.
---
The Arrhenius equation is given by:
k=Ae−EaRT
where:
- k is the rate constant,
- A is the pre-exponential factor,
- Ea is the activation energy,
- R is the universal gas constant (8.314 J/mol·K),
- T is the temperature in Kelvin.
The activation energy without the catalyst is given as:
Ea=100 kJ/mol=100,000 J/mol
The catalyst lowers the activation energy by 75%. Therefore, the new activation energy (E′a) with the catalyst is:
E′a=Ea−0.75×Ea=100,000−0.75×100,000=25,000 J/mol
- The rate constant without the catalyst (k1):
k1=Ae−100,000RT
- The rate constant with the catalyst (k2):
k2=Ae−25,000RT
To find the effect of the catalyst on the rate of reaction, we need the ratio k2k1:
k2k1=Ae−25,000RTAe−100,000RT=e−25,000RT+100,000RT=e75,000RT
Now, we substitute R=8.314 J/mol⋅K and T=20∘C=293 K:
k2k1=e75,0008.314×293
Calculating the exponent:
75,0008.314×293≈75.0
Thus,
k2k1=e75.0
The ratio of the rates of reaction (R2R1) is equal to the ratio of the rate constants:
R2R1=k2k1=e75.0
This indicates that the rate of reaction in the presence of the catalyst is significantly higher than in its absence.
The presence of the catalyst increases the rate of reaction by a factor of e75.0, which is a very large number, indicating a dramatic increase in the rate of reaction.
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Solved Example
52 Videos
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Ex 4.1 (Objective)
9 Videos
- CARBOXYLIC ACIDS AND THEIR DERIVATIVESBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CARBOXYLIC ACIDS AND THEIR DERIVATIVESEXERCISE - Exercises Archives (Analytical And Descriptive)
34 Videos
- COORDINATION COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - COORDINATION COMPOUNDSEXERCISE - Archives Subjective
18 Videos
Similar Questions
The energy of activation for ab uncatalysed reaction is 100KJmol−1 presence of a catalyst lowers the energy of activation by 75% . The log10.K2K1 of the ratio of rate constant of catalysed and uncatalysed reactions at 27∘C is ?
Assume the frequency factor is same for both reactions. ( Given 2.303×8.314=19.147)
View SolutionWith 100 kJ mol- activation energy for an uncatalysed reaction at 20°C, the catalyst lowers the energy of activation by 75%. What will be the effective rate if other conditions are same?
View SolutionThe major product of the following reaction is:
View SolutionThe activation energy for a first order reaction is 60 kJ mol−1 in the absence of a catalyst and 50 kJ mol−1 in the presence of a catalyst. How many times will the rate of reaction grow in the presence of the catalyst if the reaction proceeds at 27∘C ?
View SolutionThe activation energy for a first order reaction is 60 kJ mol−1 in the absence of a catalyst and 50 kJ mol−1 in the presence of a catalyst. How many times will the rate of reaction grow in the presence of the catalyst if the reaction proceeds at 27∘C ?
View SolutionThe activation energy for a first order reaction is 60 kJ mol−1 in the absence of a catalyst and 50 kJ mol−1 in the presence of a catalyst. How many times will the rate of reaction grow in the presence of the catalyst if the reaction proceeds at 27∘C ?
View SolutionThe activation energy of
H2+I2⇔2HI(g) in equilibrium for the forward reaction is 167kJmol−1 whereas for the reverse reaction is 180kJmol−1. The presence of catalyst lowers the activation energy by 80kJmol−1. Assuming that the reactions are made at 27∘C and the frequency factor for forwatd and backward reactions are 4×10−4 and 2×10−3 respectively, calculate Kc.
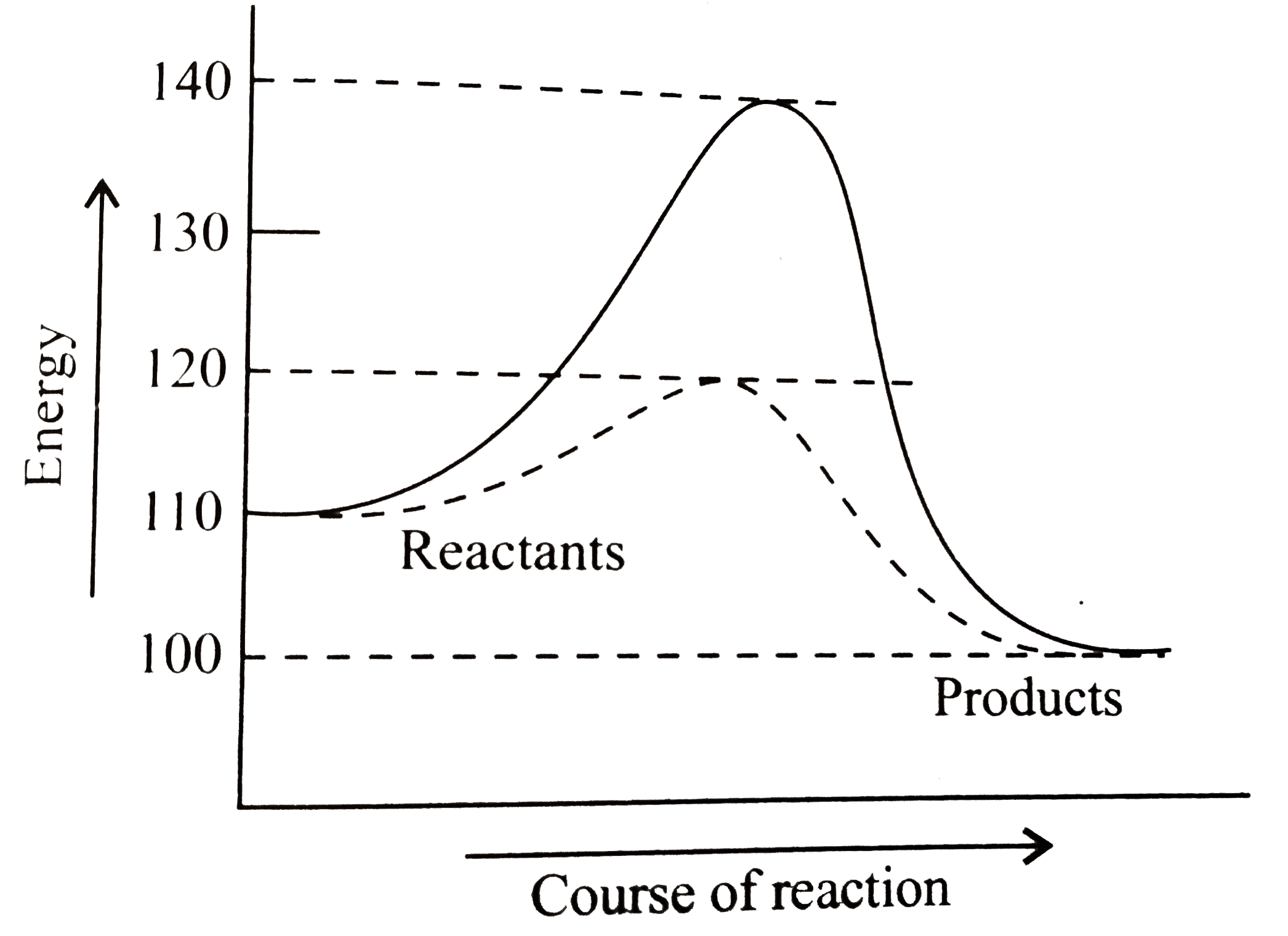
View SolutionRefer picture given below.
(a) Calculate ΔH for the reaction and the energy of activation for the forward reaction as well as backward reaction.
(b) The dotted curve is in the presence of a catalyst. What is the energy of activation for the two reactions in the presence of catalyst?
( c) Will the catalyst change the extent of reaction?
View SolutionThe activation energy of a first order reaction at 300K is 60 kJmol−1. In the presence of a catalyst, the activation energy gets lowered to 50kJmol−1 at 300K. How many times the reaction rate change in the presence of a catalyst at the same temperature ?
View SolutionHow is the reaction rate influenced by energy of activation ?
View Solution
