The efficiency of a fuel cell si 80% and the standard heat of reaction is −300kJ. The reaction involves two electrons in redox change. Ec− for the cell is
(a)1.24V
(b)2.48V
(c)0V
(d)0.62V
1.24V
2.48V
0V
0.62V
The correct Answer is:a
To solve the problem, we need to find the standard cell potential E∘ for a fuel cell given its efficiency, standard heat of reaction, and the number of electrons involved in the redox change. Here’s how to approach the problem step by step:
Step 1: Understand the relationship between efficiency, Gibbs free energy, and enthalpy.
The efficiency of the fuel cell can be expressed as:
Efficiency=ΔG∘ΔH∘
Given that the efficiency is 80%, we can write:
0.80=ΔG∘ΔH∘
Step 2: Convert the standard heat of reaction to joules.
The standard heat of reaction is given as −300 kJ. We need to convert this to joules:
ΔH∘=−300×103 J=−300000 J
Step 3: Calculate ΔG∘.
Using the efficiency equation:
ΔG∘=0.80×ΔH∘
Substituting the value of ΔH∘:
ΔG∘=0.80×(−300000)=−240000 J
Step 4: Relate Gibbs free energy to cell potential.
The relationship between Gibbs free energy, cell potential, and the number of electrons is given by:
ΔG∘=−nFE∘
Where:
- n = number of moles of electrons (given as 2)
- F = Faraday's constant (96500 C/mol)
- E∘ = standard cell potential
Step 5: Rearrange the equation to find E∘.
Rearranging the equation gives:
E∘=−ΔG∘nF
Substituting the values:
E∘=−−2400002×96500
Step 6: Calculate E∘.
Calculating the above expression:
E∘=240000193000≈1.24 V
Conclusion:
The standard cell potential E∘ for the fuel cell is approximately 1.24 V. Therefore, the correct answer is:
(a) 1.24 V
The efficiency of the fuel cell can be expressed as:
Efficiency=ΔG∘ΔH∘
Given that the efficiency is 80%, we can write:
0.80=ΔG∘ΔH∘
The standard heat of reaction is given as −300 kJ. We need to convert this to joules:
ΔH∘=−300×103 J=−300000 J
Using the efficiency equation:
ΔG∘=0.80×ΔH∘
Substituting the value of ΔH∘:
ΔG∘=0.80×(−300000)=−240000 J
The relationship between Gibbs free energy, cell potential, and the number of electrons is given by:
ΔG∘=−nFE∘
Where:
- n = number of moles of electrons (given as 2)
- F = Faraday's constant (96500 C/mol)
- E∘ = standard cell potential
Rearranging the equation gives:
E∘=−ΔG∘nF
Substituting the values:
E∘=−−2400002×96500
Calculating the above expression:
E∘=240000193000≈1.24 V
The standard cell potential E∘ for the fuel cell is approximately 1.24 V. Therefore, the correct answer is:
(a) 1.24 V
Topper's Solved these Questions
- ELECTROCHEMISTRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ELECTROCHEMISTRYEXERCISE - Exerciseassertion -Reasoning
25 Videos
- ELECTROCHEMISTRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ELECTROCHEMISTRYEXERCISE - Exerciseinterger
8 Videos
- ELECTROCHEMISTRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ELECTROCHEMISTRYEXERCISE - Exercisemultiple Correct Ansers
53 Videos
- D AND F BLOCK ELEMENTSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - D AND F BLOCK ELEMENTSEXERCISE - Archives Subjective
29 Videos
- GENERAL PRINCIPLES AND PROCESS OF ISOLATION OF ELEMENTSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - GENERAL PRINCIPLES AND PROCESS OF ISOLATION OF ELEMENTSEXERCISE - Archives (Subjective)
14 Videos
Similar Questions
The standard emf of a galvanic cell involving 2 motes of electrons in its redox reaction is 0.59 V the equilibriun constant for the redox reaction of the cell is
View SolutionThe standard EMF of quinhydrone is 0.699V. The EMF of the quinhydrone electrode dipped in a solution with pH=10 is
(a)0.109V
(b)−0.109V
(c)1.289V
(d)−1.289V
View SolutionAt 25∘C, the standard emf of a cell having reaction involving two electrons change is found to be 0.295 V. The equilibrium constant of the reaction is :
View SolutionThe standard potential of a cell using the reaction
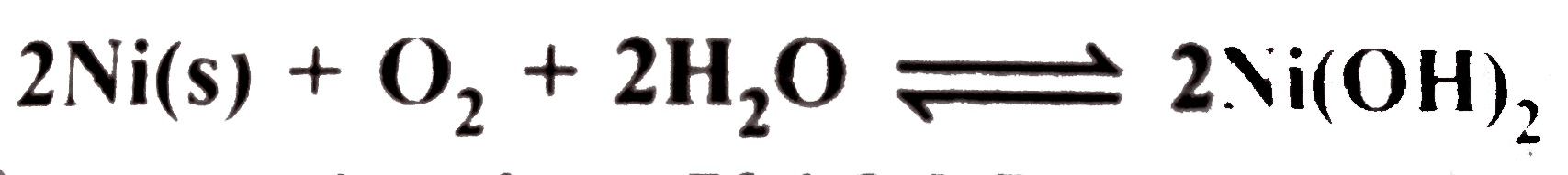 is 1.12. The heat of the reaction is −504.2kJmol−1 at 25∘C. Calculate the entropy change.
is 1.12. The heat of the reaction is −504.2kJmol−1 at 25∘C. Calculate the entropy change.
View SolutionThe Ecell for a given cell is 1.2346 and 1.2340V at 300K and 310K, respectively. Calculate the change in entropy during the cell reaction if the redox change involves three electrons.
View SolutionCalculate Ec− for the reactions :
ZnY2−⇔Zn(s)+Y4− where Y4− is the completely deprotonated anion of EDTA. The formation constant forZnY2− is 3.2×1016 and Ec− for Zn→Zn2++2e− is 0.76V.
(a)−1.25V
(b)0.48V
(c)+0.68V
(d)−0.27V
View SolutionIf standard emf (E∘) of a half -cell Y2+/Y+ is 0.15 V, the standard emf of the half cell Y+/Y will be ? Given that the standard emf of cell of full cell is 0.34V.
View SolutionThe magnitude ( but not the sign ) of the standard reduction potentials of two metals X and Y are :
Y2+2e−→Y∣∣Ec−1∣∣=0.34V
X2+2e−→X∣∣Ec−2∣∣=0.25V
When the two half cells of X and Yare connected to construct a cell, electrons flow from X to Y. When X is connected to a standard hydrogen electrode (SHE),electrons flow from X to SHE.
If standard emf (Ec−) of a half cell Y2∣Y⊕ is 0.15V, the standard emf of the half cell Y⊕∣Y will be
(a)0.19V
(b)0.53V
(c)0.49V
(d)0.64V
View SolutionCalculate the standard free energy change in kJ for the reaction Cu++I−→CuI Given:
CuI+e→Cu+I−E0=−0.17V
Cu++e→CuE0=0.53V
View SolutionThe standard E∘redValues if A, B and C are +0.68V, -0.76V, −0.50V respectively.
The order of their reducing power is :
View Solution
