Mechanism of the reaction is:
A2k⇐⇒k'2A
A+B2k2−−→C+B
B+A2k2−−→C+A
What is−d[A2]dt
To find the expression for −d(A2)dt based on the given reaction mechanism, we need to analyze the contributions from each reaction step involving A2.
1. Identify the Reactions:
The mechanism consists of three reactions:
- A2k⇌k′2A
- A+B2k2→C+B
- B+A2k2→C+A
2. Write the Rate Expression for the First Reaction:
For the first reaction, we can write the rate of change of A2 as:
−d(A2)dt=k(A2)−k′(A)2
Here, k is the forward rate constant, and k′ is the backward rate constant. The term k′(A)2 arises because two moles of A are produced when one mole of A2 is consumed.
3. Consider the Second Reaction:
The second reaction does not directly involve A2, so it does not contribute to the rate of change of A2.
4. Write the Rate Expression for the Third Reaction:
For the third reaction, the rate of disappearance of A2 is given by:
−d(A2)dt=k2(B)(A2)
Here, k2 is the rate constant for the reaction, and it involves the concentration of B and A2.
5. Combine the Expressions:
Now, we can combine the contributions from the first and third reactions to get the overall rate of change of A2:
−d(A2)dt=k(A2)−k′(A)2+k2(B)(A2)
6. Final Expression:
Thus, the final expression for the rate of disappearance of A2 is:
−d(A2)dt=k(A2)+k2(B)(A2)−k′(A)2
The mechanism consists of three reactions:
- A2k⇌k′2A
- A+B2k2→C+B
- B+A2k2→C+A
For the first reaction, we can write the rate of change of A2 as:
−d(A2)dt=k(A2)−k′(A)2
Here, k is the forward rate constant, and k′ is the backward rate constant. The term k′(A)2 arises because two moles of A are produced when one mole of A2 is consumed.
The second reaction does not directly involve A2, so it does not contribute to the rate of change of A2.
For the third reaction, the rate of disappearance of A2 is given by:
−d(A2)dt=k2(B)(A2)
Here, k2 is the rate constant for the reaction, and it involves the concentration of B and A2.
Now, we can combine the contributions from the first and third reactions to get the overall rate of change of A2:
−d(A2)dt=k(A2)−k′(A)2+k2(B)(A2)
Thus, the final expression for the rate of disappearance of A2 is:
−d(A2)dt=k(A2)+k2(B)(A2)−k′(A)2
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Solved Example
52 Videos
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Ex 4.1 (Objective)
9 Videos
- CARBOXYLIC ACIDS AND THEIR DERIVATIVESBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CARBOXYLIC ACIDS AND THEIR DERIVATIVESEXERCISE - Exercises Archives (Analytical And Descriptive)
34 Videos
- COORDINATION COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - COORDINATION COMPOUNDSEXERCISE - Archives Subjective
18 Videos
Similar Questions
Mechanism of the reaction is:
A2k2⇐⇒2A
A+Bk2−−→C
A2+Ck−−→D+A
What is d[D]dt ?
View SolutionMechanism of the reaction is:
Ak1−−→B,2Ak2−−→C+D
What is −d[A]dt ?
View SolutionMechanism of the reaction is:
Ak2⇐⇒k1B ...(i)
B+Ak3⇐⇒C ...(ii)
¯¯¯¯¯¯¯¯¯¯¯¯¯¯2A→C––––––––– ...(iii)
What is (a) −d[A]dt, (b ) d[C]dt
View SolutionThe mechanism of the reaction
2NO+O2→2NO2 is
NO+NOk1⇐⇒k−1N2O2(fast)
N2O2+O2k2−−→2NO2(slow)
The rate constant of the reaction is
View SolutionConisder the following reactions:
I. A+Bk1⇐⇒k−1C
II. C+Bk2−−→D
Then k1[A][B]−k−1[C]−k2[C][B] is equal to
(a) −d[A]dt
(b)−d[B]dt
(c)d[C]dt
(d)d[D]dt
View Solution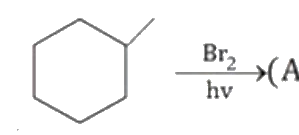 Br2−−→hv(A)alc. KOH−−−−→(B)OsO4−−→(C)HlO4−−→(D), Identify 'D'
Br2−−→hv(A)alc. KOH−−−−→(B)OsO4−−→(C)HlO4−−→(D), Identify 'D'
View SolutionA proposed mechanism for a reaction A→B is
Ak1⇐⇒k2C Ck3⇐⇒k4B
Determine the expresison for the equilibrium constant for the overall reaction in terms of the rate constants.
View SolutionSOCl2−−−→(A)KCN−−→(B)H+−−→(C ), the compound (C ) is

View SolutionFor an elementary chemical reaction, A2k1⇐===⇒k−12A, the expression for d[A]dt is
View SolutionFor an elementary chemical reaction, A2k1⇐===⇒k−12A, the expression for d[A]dt is
View Solution
