Figure shows a wire ring of radius a that is perpendicular to the general direction of a radially sysmmetric, diverging magnetic field. The magnetic field at the ring is everywhere of the same magnitude B, and its direction at the ring everywhere makes an angle with a normal to the plane of the ring. thge twisted lead wires have no effect on the problem. Find the magnitude of the force the field exerts on the ring if the ring carries a current i.

For the first order reaction , half life and for the second order reaction , half life
But (given)
...(i)
a. Rate at the start of reaction ...first order and aret at the start of reaction ...second order
Hence by Eq. (i)
Rate after one half life when the concentration of the reactant is reduced to
for reaction
and for reaction
Hence,
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Solved Example
52 Videos
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Ex 4.1 (Objective)
9 Videos
- CARBOXYLIC ACIDS AND THEIR DERIVATIVESBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CARBOXYLIC ACIDS AND THEIR DERIVATIVESEXERCISE - Exercises Archives (Analytical And Descriptive)
34 Videos
- COORDINATION COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - COORDINATION COMPOUNDSEXERCISE - Archives Subjective
18 Videos
Similar Questions
In the figure shown, the magnet is pushed towards the fixed ring along the axis of the ring and it passes through the ring.
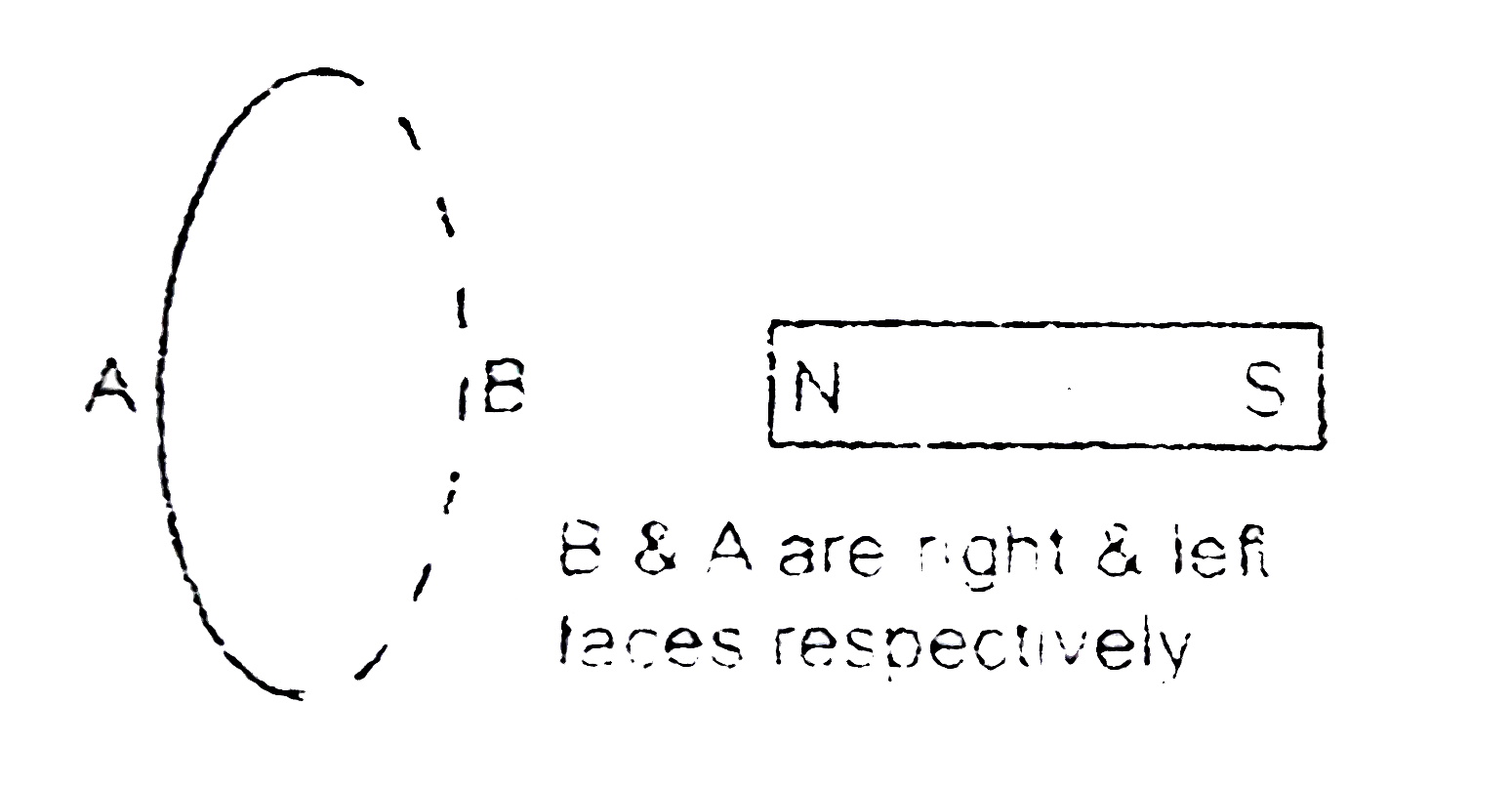
View SolutionFind the magnitude and direction of magnetic field at point P due to the current carrying wire as shown in

View SolutionFind the radius of gyration of a circular ring of radius r about a line perpendicular to the plane of the ring and passing through one of this particles.
View SolutionA neutral metallic ring is placed in a circular symmetrical uniform magnetic field with its plane perpendicular to the field.If the magnitude of field starts increasing with time, then:
View SolutionA circular conducting ring is rotated about one of its diameter in a magnetic field
View SolutionThere is a ring of radius r having linear charge density λ and rotating with a uniform angular velocity ω. the magnetic field produced by this ring at its own centre would be
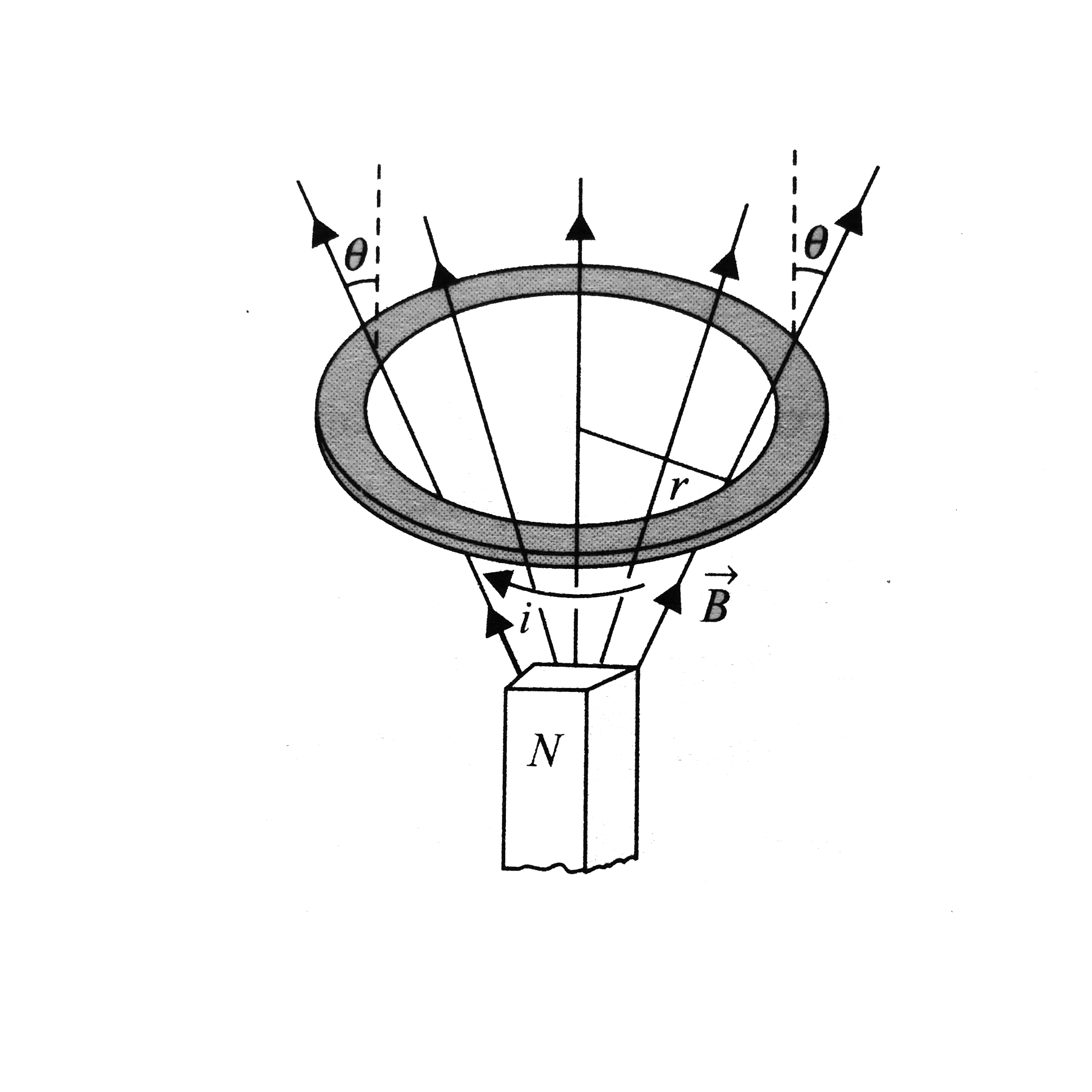
View SolutionA strong magnet is placed under a horizontal conducting ring of radius r that carries current i as shown in Fig. If the magnetic field makes an angle θ with the vertical at the ring's location, what are the magnitude and direction of the resultant force on the ring?
View SolutionA vertical conducting ring ogradius R falls vertically in a horizontal magnetic field of magnitude B. The direction of B is perpendicular to the plane of the ring. When the speed of the ring is v,

View SolutionA conducting ring of radius r and resistance R is placed in region of uniform time varying magnetic field B which is perpendicular to the plane of the ring. It the magnetic field is changing at a rate α, then the current induced in the ring is
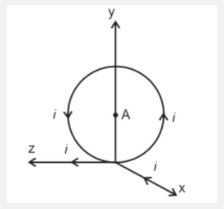
View SolutionA ring of the radius R is placed in the y - z plane and it carries a current i. The conducting wires which are used to supply the current to the ring can be assumed to be vary long and are placed as shown in the figure. The magnitude of the magnetic field at the centre of the ring A is
View Solution
