A neutral metallic ring is placed in a circular symmetrical uniform magnetic field with its plane perpendicular to the field.If the magnitude of field starts increasing with time, then:
the ring starts translating
the ring starts rotating about its axis
the ring slightly contracts
the ring starts rotating about a diameter
The correct Answer is:C
To solve the problem, we need to analyze the behavior of a neutral metallic ring placed in a circular symmetrical uniform magnetic field, particularly when the magnetic field's magnitude starts increasing with time.
1. Understanding the Setup:
- We have a neutral metallic ring in a uniform magnetic field.
- The plane of the ring is perpendicular to the magnetic field.
2. Magnetic Field Change:
- The magnetic field B is increasing with time, which implies dBdt>0.
3. Induced EMF and Current:
- According to Faraday's law of electromagnetic induction, a changing magnetic field through a closed loop induces an electromotive force (EMF) in that loop.
- The induced EMF (E) can be calculated using the formula:
E=−dΦBdt
- Where ΦB is the magnetic flux given by ΦB=B⋅A (with A being the area of the ring).
4. Direction of Induced Current:
- The direction of the induced current can be determined using Lenz's Law, which states that the induced current will flow in a direction that opposes the change in magnetic flux.
- Since the magnetic field is increasing, the induced current will flow in a direction that creates a magnetic field opposing the increase.
5. Force on the Ring:
- The induced current creates a magnetic moment m in the ring.
- The force on a current-carrying conductor in a magnetic field is given by F=IL×B.
- For a closed loop (the ring), the net force is zero because the lengths of the segments cancel out.
6. Torque on the Ring:
- The torque τ on the ring due to the magnetic field is given by:
τ=m×B
- Since the plane of the ring is perpendicular to the magnetic field, the angle θ between m and B is zero, leading to:
τ=mBsin(0)=0
- Therefore, there is no torque acting on the ring, meaning it cannot rotate.
7. Contraction of the Ring:
- The ring will try to oppose the increase in magnetic flux through it.
- To reduce the magnetic flux, the ring can contract, which decreases its area A and thus the magnetic flux ΦB.
8. Conclusion:
- The ring does not translate or rotate, but it may contract in response to the increasing magnetic field.
Final Answer:
The correct option is that the ring will contract.
- We have a neutral metallic ring in a uniform magnetic field.
- The plane of the ring is perpendicular to the magnetic field.
- The magnetic field B is increasing with time, which implies dBdt>0.
- According to Faraday's law of electromagnetic induction, a changing magnetic field through a closed loop induces an electromotive force (EMF) in that loop.
- The induced EMF (E) can be calculated using the formula:
E=−dΦBdt
- Where ΦB is the magnetic flux given by ΦB=B⋅A (with A being the area of the ring).
- The direction of the induced current can be determined using Lenz's Law, which states that the induced current will flow in a direction that opposes the change in magnetic flux.
- Since the magnetic field is increasing, the induced current will flow in a direction that creates a magnetic field opposing the increase.
- The induced current creates a magnetic moment m in the ring.
- The force on a current-carrying conductor in a magnetic field is given by F=IL×B.
- For a closed loop (the ring), the net force is zero because the lengths of the segments cancel out.
- The torque τ on the ring due to the magnetic field is given by:
τ=m×B
- Since the plane of the ring is perpendicular to the magnetic field, the angle θ between m and B is zero, leading to:
τ=mBsin(0)=0
- Therefore, there is no torque acting on the ring, meaning it cannot rotate.
- The ring will try to oppose the increase in magnetic flux through it.
- To reduce the magnetic flux, the ring can contract, which decreases its area A and thus the magnetic flux ΦB.
- The ring does not translate or rotate, but it may contract in response to the increasing magnetic field.
The correct option is that the ring will contract.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 1
14 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 2
17 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-1
63 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Advanced level problems
31 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - HLP
40 Videos
Similar Questions
A charged particle enters a uniform magnetic field perpendicular to it. The magnetic field
View SolutionA conducting circular loop is placed is a uniform magnetic field B =0.20 T with its plane perpendicular to the field . Somehow, the radius of the loop starts shrinking at a constant rate of 1.0mms−1. Find the induced emf in the loop at an instant when the radius is 2 cm.
View Solution
Knowledge Check
A conducting ring is placed in a uniform magnetic field with its plane perpendicular to the field . An emf is induced in the ring if
Ait is rotated about its axis.Bit is rotated about its diameter.Cit is not moved.Dit is given translational motion in the field.In a uniform magnetic field, the field lines are :
AcurvedBparallel and equidistant straight linesCparallel, but non-equispaced straight linesDnothing can be said.
A uniform but time varying magnetic field is present in a circular region of radius R. The magnetic field is perpendicular and into the plane of the loop and the magnitude of field is increasing at a constant rate α. There is a straight conducting rod of length 2R placed as shown in figure.
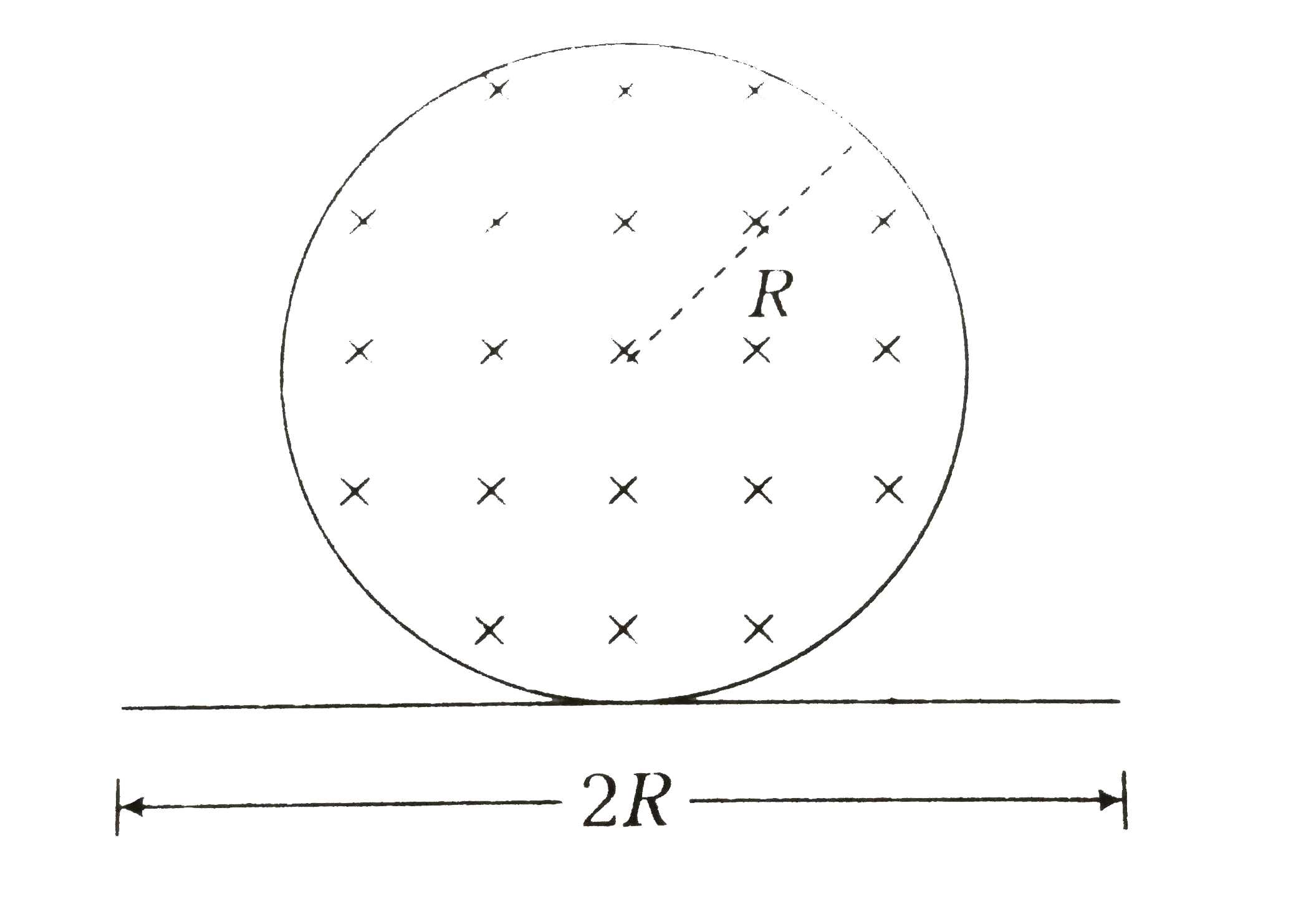
The magnitude of induced emf across the rod is
View SolutionWhen a current carrying coil is placed in a uniform magnetic field with its magnetic moment anti-parallel to the field.
View SolutionWhen a current carrying coil is placed in a uniform magnetic field with its magnetic moment anti-parallel to the field.
View SolutionA rectangular copper coil is placed in a uniform magnetic field of induction 40 mT with its plane perpendicular to the field. The area of the coil is shrinking at a constant rate of 0.5m2s−1. The emf induced in the coil is
View SolutionA conducting ring of radius r and resistance R is placed in region of uniform time varying magnetic field B which is perpendicular to the plane of the ring. It the magnetic field is changing at a rate α, then the current induced in the ring is
View SolutionA conducting square loop is placed in a magnetic field B with its plane perpendicular to the field. Now the sides of the loop start shrinking at a constant rate α. the induced emf in the loop at an instant when its side is a is
View Solution
