Find out the percentage of the reactant molecules crosisng over the energy barrier at 325K.
Given: ΔH325K=0.12kcal,
Ea(b)=0.02kcal
80.65%
70.65%
60.65%
50.65%
The correct Answer is:A
To solve the problem of finding the percentage of reactant molecules crossing over the energy barrier at 325 K, we will follow these steps:
Step 1: Identify Given Data
We have the following data:
- ΔH325K=0.12kcal
- Ea(b)=0.02kcal
Step 2: Calculate Activation Energy for Forward Reaction
Using the relationship:
ΔH=Ef−Eb
we can rearrange it to find the activation energy for the forward reaction (Ef):
Ef=ΔH+Eb
Substituting the values:
Ef=0.12kcal+0.02kcal=0.14kcal
Step 3: Convert Activation Energy to Calories
Since we will use the gas constant R in calories, we convert Ef from kilocalories to calories:
Ef=0.14kcal×1000=140cal
Step 4: Use the Arrhenius Equation
The fraction of molecules (x) crossing over the energy barrier can be calculated using the Arrhenius equation:
x=e−EaRT
Where:
- Ea=Ef=140cal
- R=2cal/(mol K)
- T=325K
Step 5: Calculate the Exponent
Substituting the values into the equation:
x=e−1402×325=e−140650=e−0.2153846154
Step 6: Calculate the Value of x
Calculating the exponent:
x≈e−0.2154≈0.8063
Step 7: Convert Fraction to Percentage
To find the percentage of reactant molecules:
Percentage=x×100≈0.8063×100≈80.63%
Step 8: Final Answer
The percentage of the reactant molecules crossing over the energy barrier at 325 K is approximately 80.6%.
---
We have the following data:
- ΔH325K=0.12kcal
- Ea(b)=0.02kcal
Using the relationship:
ΔH=Ef−Eb
we can rearrange it to find the activation energy for the forward reaction (Ef):
Ef=ΔH+Eb
Substituting the values:
Ef=0.12kcal+0.02kcal=0.14kcal
Since we will use the gas constant R in calories, we convert Ef from kilocalories to calories:
Ef=0.14kcal×1000=140cal
The fraction of molecules (x) crossing over the energy barrier can be calculated using the Arrhenius equation:
x=e−EaRT
Where:
- Ea=Ef=140cal
- R=2cal/(mol K)
- T=325K
Substituting the values into the equation:
x=e−1402×325=e−140650=e−0.2153846154
Calculating the exponent:
x≈e−0.2154≈0.8063
To find the percentage of reactant molecules:
Percentage=x×100≈0.8063×100≈80.63%
The percentage of the reactant molecules crossing over the energy barrier at 325 K is approximately 80.6%.
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Exercises Linked Comprehension
59 Videos
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Exercises Multiple Correct
33 Videos
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Ex 4.3 More Than One Correct
5 Videos
- CARBOXYLIC ACIDS AND THEIR DERIVATIVESBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CARBOXYLIC ACIDS AND THEIR DERIVATIVESEXERCISE - Exercises Archives (Analytical And Descriptive)
34 Videos
- COORDINATION COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - COORDINATION COMPOUNDSEXERCISE - Archives Subjective
18 Videos
Similar Questions
Find the values of k if area of triangle is 4 sq. units and vertices are: (k,0),(0,2)(4,0)
View SolutionCalculate the lattice energy from the following data (given 1eV=23.0kcalmol−1)
i. ΔfHɵ(KI)=−78.0kcalmol−1
ii. IE1 of K=4.0eV
iii. ΔdissHɵ(I2)=28.0kcalmol−1
iv. ΔsubHɵ(K)=20.0kcalmol−1
v. EA of I=−70.0kcalmol−1
vi. ΔsubHɵ of I2=14.0kcalmol−1
View SolutionGibbs-Helmoholtz equation relates the free energy change to the enthalpy and entropy changes of the process as
(ΔG)PT=ΔH−TΔS
The magnitude of ΔH does not change much with the change in temperature but the enrgy factor TΔS changes appreciably. Thus, spontaneity of a process depends very much on temperature.
For the reaction at 298K,2A+B→C
ΔH=100kcal and ΔS=0.020kcalK−1. If ΔH and ΔS are assumed to be constant over the temperature range, at what temperature will the reaction become spontaneous?
View SolutionFrom the following data at 25∘C, calculate the bond energy of O – H bond:
(i) H2(g)→2H(g),ΔH1=104.2kcal
(ii) O2(g)→2O(g),ΔH2=118.4kcal
(iii) H2(g)+12O2(g)→H2O(g),ΔH3=−57.8kcal
View SolutionCalculate the enthalpy of formation of acetic acid from the following data.
CH3COOH(l)+202(g)—2C02(g)+2H2O(l), ΔH=−207.9 kcal
C(s)+O2(g)—C02(g)...(ii)ΔH=−94.48 kcal
H2(g)+12O2(g)→H2O(l), ΔH=−68.4 k cal
View SolutionA colliison between reactant molecules must occur with a certain minimum energy before it is effective in yielding Product molecules. This minimum energy is called activation energy Ea Large the value of activation energy, smaller the value of rate constant k. Larger is the value of activation energy, greater is the effect of temperature rise on rate constant k.
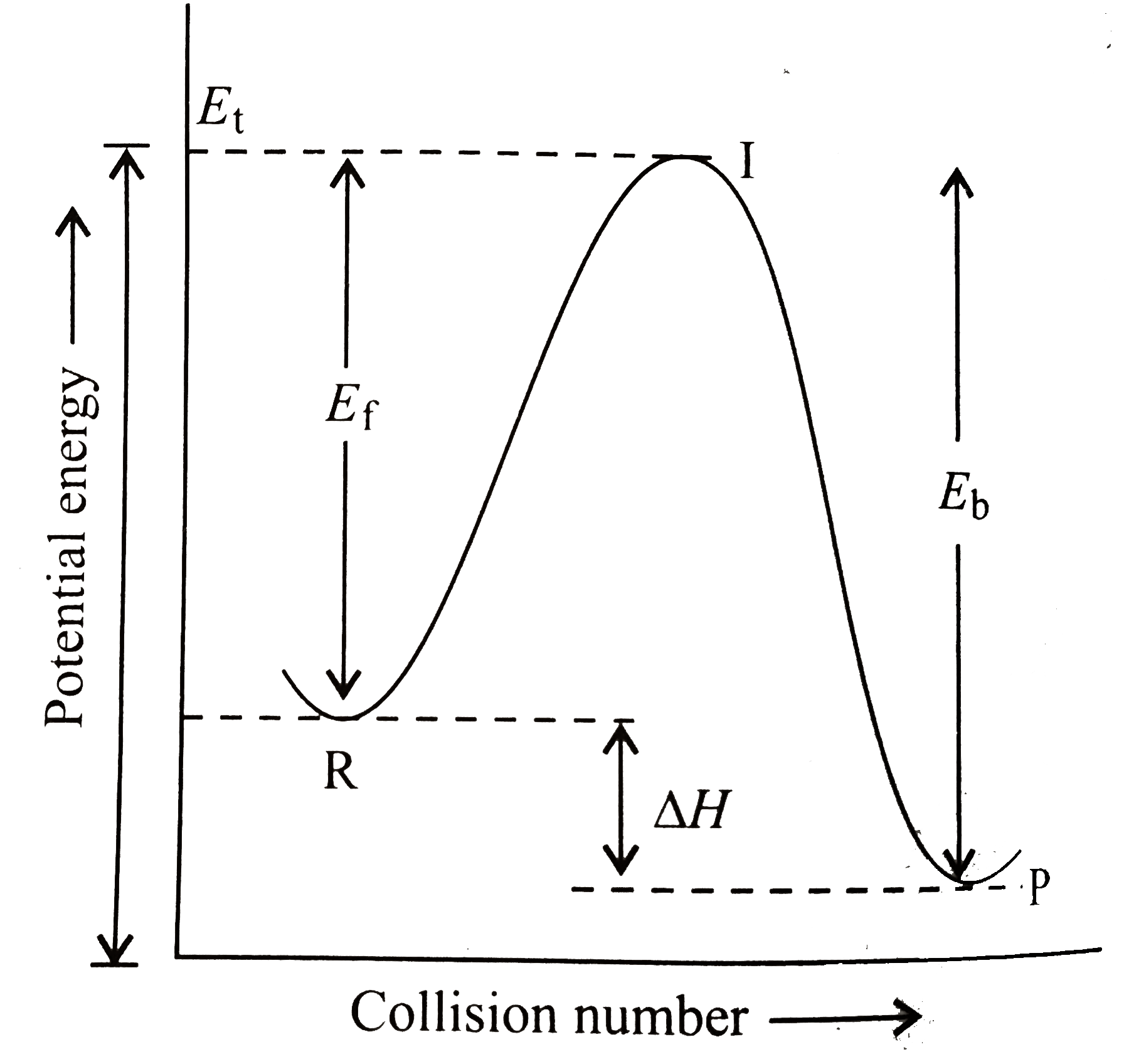
Ef= Activation energy of forward reaction
Eb= Activation energy of backward reaction
ΔH=Ef−Eb
Ef= threshold energy
The rate constant of a certain reaction is given by k=Ae−Ea/RT
(where A= Arrhenius constant). Which factor should be lowered so that the rate of reaction may increase?
View SolutionIf the circumcentre of the triangle whose vertices are (0,2),(3,5)and(5,8)is (h,k) then 4(h2+k2) equals_____.
View SolutionA colliison between reactant molecules must occur with a certain minimum energy before it is effective in yielding Product molecules. This minimum energy is called activation energy Ea Large the value of activation energy, smaller the value of rate constant k. Larger is the value of activation energy, greater is the effect of temperature rise on rate constant k.
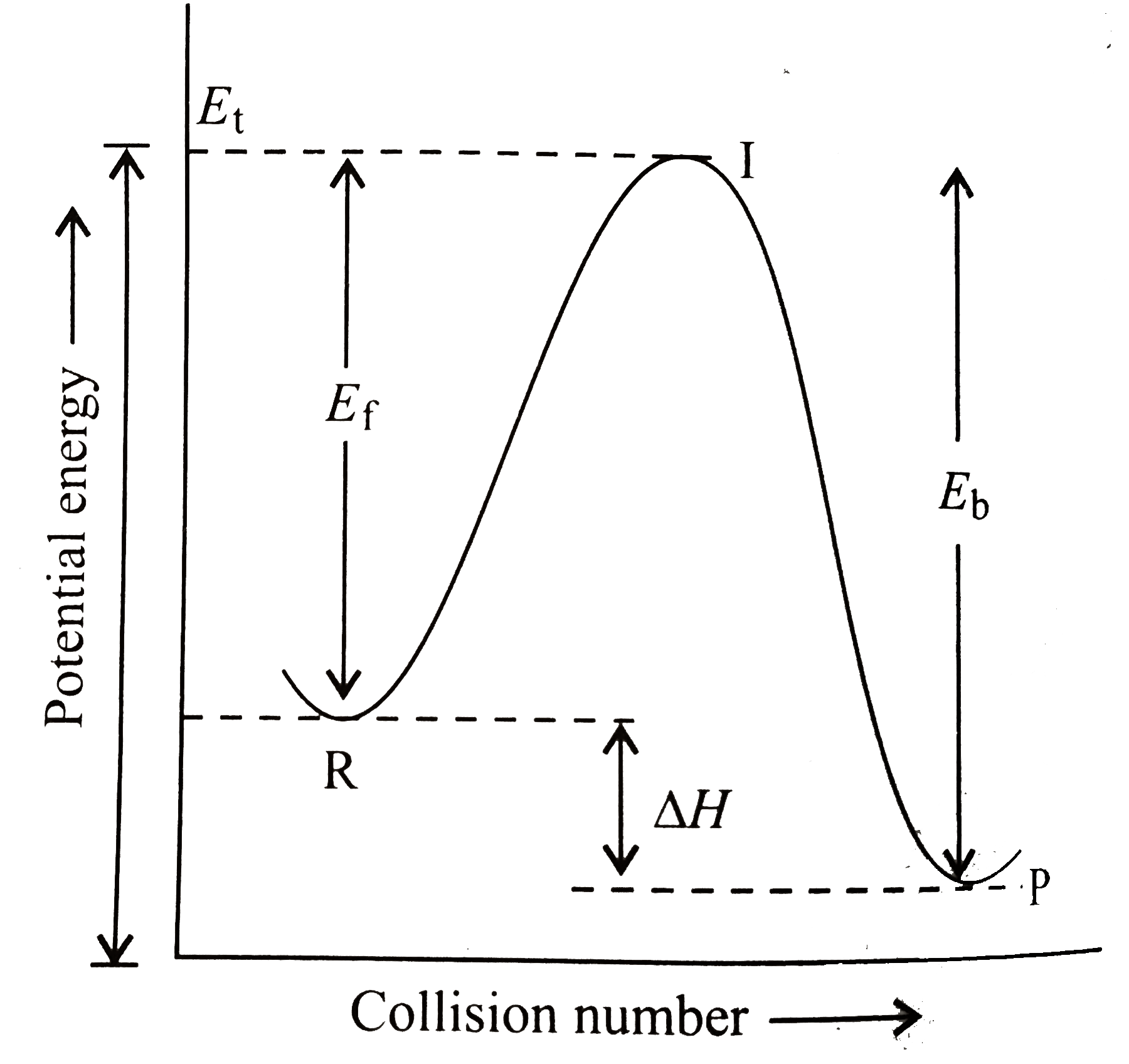
Ef= Activation energy of forward reaction
Eb= Activation energy of backward reaction
ΔH=Ef−Eb
Ef= threshold energy
For two reactions, activation energies are Ea1 and Ea2, rate constant are k1 and k2 at the same temperature. If k1>k2, then
View SolutionA colliison between reactant molecules must occur with a certain minimum energy before it is effective in yielding Product molecules. This minimum energy is called activation energy Ea Large the value of activation energy, smaller the value of rate constant k. Larger is the value of activation energy, greater is the effect of temperature rise on rate constant k.

Ef= Activation energy of forward reaction
Eb= Activation energy of backward reaction
ΔH=Ef−Eb
Ef= threshold energy
The activation eneries for forward and backward reactions in a chemical reaction are 30.5 and 45.4kJmol−1 respectively. The reaction is
View SolutionEthanol was oxidised to acetic acid in a catalyst chamber at 18∘C. Calculate the rate of removel of heat to maintain the reaction chamber at 18∘C with the feed rate of 30kgh−1 ethanol along with excess oxygen to the system at 18∘C, given that a 42mol% yield based on ethanol is obtained. Given that
ΔfHΘ'H2O(l)=−68.0kcalmol−1
ΔfHΘ'C2H5OH(l)=−66kcalmol−1
ΔfHΘ'CH3COOH(l)=−118kcalmol−1
View Solution
