Conisder the following reaction at 300K:
A→B (uncatalyzed reaction)
A→B (catalyzed reaction)
The activation energy is lowered by 8.314kJmol−1 for the catalyzed reaction. The rate of this reaction is
15 times
38 times
22 times
28 times
The correct Answer is:D
To solve the problem regarding the rate of the catalyzed reaction compared to the uncatalyzed reaction, we will use the Arrhenius equation and the information provided in the question.
1. Understand the Arrhenius Equation:
The Arrhenius equation is given by:
k=Ae−EaRT
where:
- k is the rate constant,
- A is the pre-exponential factor,
- Ea is the activation energy,
- R is the universal gas constant (8.314 J/mol·K),
- T is the temperature in Kelvin.
2. Define the Activation Energies:
Let:
- Ea be the activation energy for the uncatalyzed reaction,
- Eac=Ea−8.314kJ/mol be the activation energy for the catalyzed reaction (since it is lowered by 8.314 kJ/mol).
3. Write the Rate Constants:
For the uncatalyzed reaction:
k1=Ae−EaRT
For the catalyzed reaction:
k2=Ae−EacRT=Ae−Ea−8.314×103RT
4. Take the Ratio of Rate Constants:
To find the ratio of the rate constants k2k1:
k2k1=Ae−EacRTAe−EaRT=e−EacRT+EaRT=e8.314×103RT
5. Substitute Values:
Now substitute R=8.314J/mol⋅K and T=300K:
k2k1=e8.314×1038.314×300=e8.314×1032494.2=e3.33
6. Calculate e3.33:
Using a calculator:
e3.33≈28.6
Therefore, k2k1≈28.
Conclusion:
The rate of the catalyzed reaction is approximately 28 times that of the uncatalyzed reaction.
The Arrhenius equation is given by:
k=Ae−EaRT
where:
- k is the rate constant,
- A is the pre-exponential factor,
- Ea is the activation energy,
- R is the universal gas constant (8.314 J/mol·K),
- T is the temperature in Kelvin.
Let:
- Ea be the activation energy for the uncatalyzed reaction,
- Eac=Ea−8.314kJ/mol be the activation energy for the catalyzed reaction (since it is lowered by 8.314 kJ/mol).
For the uncatalyzed reaction:
k1=Ae−EaRT
For the catalyzed reaction:
k2=Ae−EacRT=Ae−Ea−8.314×103RT
To find the ratio of the rate constants k2k1:
k2k1=Ae−EacRTAe−EaRT=e−EacRT+EaRT=e8.314×103RT
Now substitute R=8.314J/mol⋅K and T=300K:
k2k1=e8.314×1038.314×300=e8.314×1032494.2=e3.33
Using a calculator:
e3.33≈28.6
Therefore, k2k1≈28.
The rate of the catalyzed reaction is approximately 28 times that of the uncatalyzed reaction.
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Exercises Linked Comprehension
59 Videos
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Exercises Multiple Correct
33 Videos
- CHEMICAL KINETICSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL KINETICSEXERCISE - Ex 4.3 More Than One Correct
5 Videos
- CARBOXYLIC ACIDS AND THEIR DERIVATIVESBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CARBOXYLIC ACIDS AND THEIR DERIVATIVESEXERCISE - Exercises Archives (Analytical And Descriptive)
34 Videos
- COORDINATION COMPOUNDSBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - COORDINATION COMPOUNDSEXERCISE - Archives Subjective
18 Videos
Similar Questions
An exothermic reaction X→Y has an activation energy of 90kJmol−1 of X and the heat of reaction is 250kJ. Find the activation energy of the reaction Y→X.
View SolutionIn an exothermic reaction X→Y, the activation energy is 100kJmol−1 of X. The enthalphy of the reaction is −140kJmol−1. The activation energy of the reverse reaction Y→X is
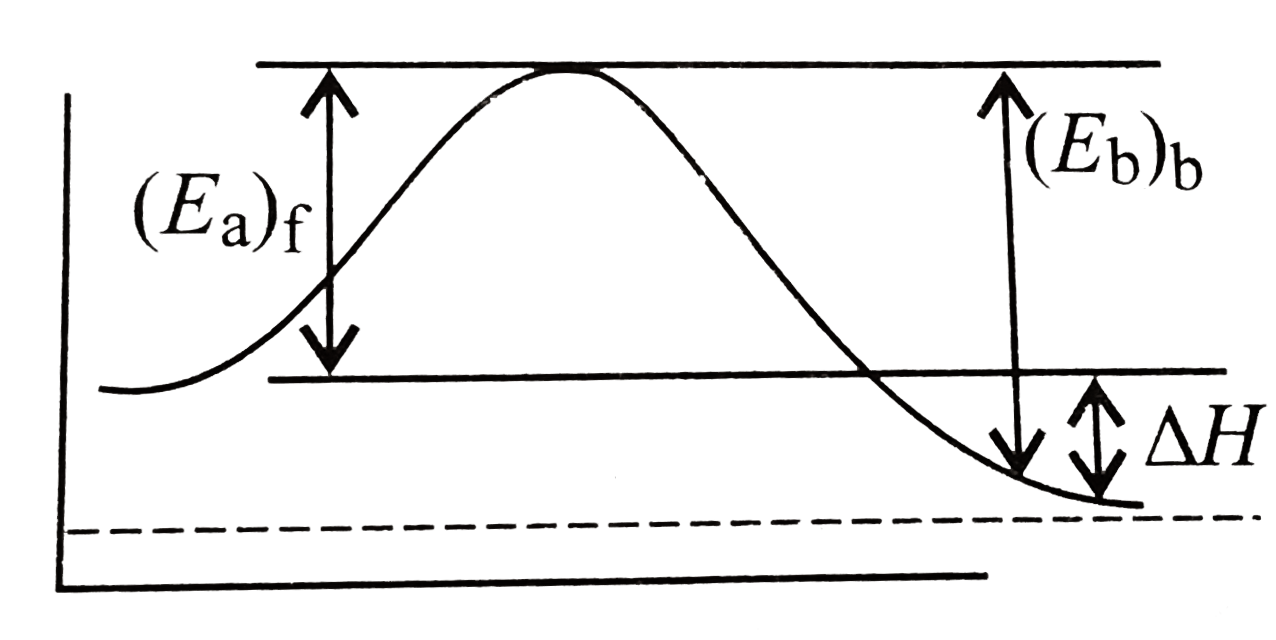
View SolutionFor an exothermic reaction A→B, the activation energy is 65kJmol−1 and enthalpy of reaction is 42kJmol−1. The activation energy for the reaction B→A will be:
View SolutionSuggest mechanisms for the following reactions which are catalyzed by strong base:
View SolutionThe activation energy of a first order reaction at 300K is 60 kJmol−1. In the presence of a catalyst, the activation energy gets lowered to 50kJmol−1 at 300K. How many times the reaction rate change in the presence of a catalyst at the same temperature ?
View SolutionThe activation energy of a reaction is zero. The rate constant of this reaction
View SolutionThe activation energy for most of the reaction is approximately 50kJmol−1. The rate for temperature coefficient for such reaction will be
View SolutionFirst step of an enzyme - catalyzed reaction is
View SolutionAn exothermic reaction, A→B, has an activation energy of 15 kcal mol−1 and the energy of reaction is 5 kcal mol−1. The activation energy in kcal mol−1 for the reaction, B→A is
View SolutionThe activation energy of a reaction is zero. Will the rate constant of the reaction depend upon temperature ?
View Solution
