In an adsorption experiment, a graph of log(x/m) versus log P was found to be linear with a slope of 45°, and the the intercept is found to be 0.3010. The amount of gas adsorbed per gram charcoal under a pressure of 0.8 atm is
1.2
1.4
1.6
1.8
The correct Answer is:C
To solve the problem, we will follow these steps:
Step 1: Understand the Freundlich Adsorption Isotherm
The Freundlich adsorption isotherm relates the amount of gas adsorbed per gram of adsorbent (x/m) to the pressure (P) of the gas. The equation can be expressed as:
xm=k⋅P1n
where:
- x = amount of gas adsorbed
- m = mass of the adsorbent
- k = Freundlich constant
- P = pressure
- n = constant related to the adsorption intensity
Step 2: Take the Logarithm of Both Sides
Taking the logarithm of both sides gives us:
log(xm)=log(k)+1nlog(P)
Step 3: Identify the Slope and Intercept
This equation resembles the equation of a straight line y=mx+c, where:
- y=log(xm)
- x=log(P)
- m=1n (slope)
- c=log(k) (intercept)
From the problem, we know:
- The slope is 45°, which means tan(45°)=1. Therefore, 1n=1 and thus n=1.
- The intercept is given as 0.3010, so log(k)=0.3010.
Step 4: Calculate the Value of k
To find k, we can convert the logarithmic value back to its exponential form:
k=100.3010
We know that 100.3010 is equal to 2 (since log10(2)≈0.3010). Therefore:
k=2
Step 5: Substitute Values into the Freundlich Equation
Now we can substitute k and the given pressure P=0.8 atm into the Freundlich equation:
xm=k⋅P1n
Substituting the values:
xm=2⋅(0.8)1
xm=2⋅0.8
xm=1.6
Conclusion
The amount of gas adsorbed per gram of charcoal under a pressure of 0.8 atm is:
xm=1.6
Final Answer
Thus, the answer is 1.6.
---
The Freundlich adsorption isotherm relates the amount of gas adsorbed per gram of adsorbent (x/m) to the pressure (P) of the gas. The equation can be expressed as:
xm=k⋅P1n
where:
- x = amount of gas adsorbed
- m = mass of the adsorbent
- k = Freundlich constant
- P = pressure
- n = constant related to the adsorption intensity
Taking the logarithm of both sides gives us:
log(xm)=log(k)+1nlog(P)
This equation resembles the equation of a straight line y=mx+c, where:
- y=log(xm)
- x=log(P)
- m=1n (slope)
- c=log(k) (intercept)
- The slope is 45°, which means tan(45°)=1. Therefore, 1n=1 and thus n=1.
- The intercept is given as 0.3010, so log(k)=0.3010.
To find k, we can convert the logarithmic value back to its exponential form:
k=100.3010
We know that 100.3010 is equal to 2 (since log10(2)≈0.3010). Therefore:
k=2
Now we can substitute k and the given pressure P=0.8 atm into the Freundlich equation:
xm=k⋅P1n
Substituting the values:
xm=2⋅(0.8)1
xm=2⋅0.8
xm=1.6
The amount of gas adsorbed per gram of charcoal under a pressure of 0.8 atm is:
xm=1.6
Thus, the answer is 1.6.
Topper's Solved these Questions
Similar Questions
In an Adsorption experiment a graph between log x/m versus log P was found to be linear with a slope of 45∘ the intercept of the log x/m was found to be 0.3010. Calculate the amount of gas adsorbed per gram of charcoal under a pressure of 0.6 bar.
View SolutionIn an adsorption experiment, a graph between log (xm) versus log P was found to be linear with a slope of 45∘ . The intercept on the log y axis was found to be 0.301 . Calculate the amount of the gas adsorbed per gram of charcoal under a pressure of 3.0 atm.
View SolutionIn an adsorption experiment a graph between log xm versus log P was fond to be linear with a slope of 45∘). The intercept on the log xm axis was found to 0.70. Calculate the amount of gas adsorbed per gram of charcoal under a pressure of 1 atm [log5=0.70]
View SolutionIn an adsorption experiment, a graph between log (xm) versus log P was found to be linear with a slope of 45∘ . The intercept on the log (xm) axis was found to be 0.3010 . Calculate the amount of the gas adsorbed per gram of charcoal under a pressure of 0.5 atm .
View SolutionFor the adsorption of a gas on a solid, the plot of log(x/m) versus log P is linear with slope equal to:
View SolutionFor the adsorption of a gas on a solid, the plot of log(x/m) versus log p is linear with slope equal to
View SolutionThe intercept on Y - axis in the graph of log xm versus log P gives
View SolutionGraph between log x/m and log P is a straight line at angle of 45∘ with intercept 0.4771 on y-axis. Calculate the amount of gas adsorbed in gram per gram of adsorbent when pressure is 3 atm.
View SolutionAdsorption of a gas on a surface follows Freundlich adsorption isotherm. Plot of log xm versus log P gives a straight line with slope equal to 0.5, then :
(xm is the mass of the gas adsorbed per gram of adsorbent)
View SolutionGraph between log(xm) and logP is straight line at angle of 45∘ with the intercept of 0.6020.
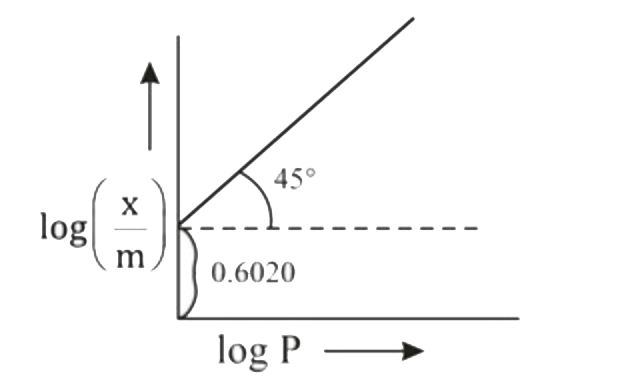
The extent of adsorption (xm) at a pressure of 1 atm is
View Solution
