IN radioactive series, an inner transition element .92U238 loses one α-particles and one β-particle to produce a very unstable daughter nuclei .91Pa234 with half life 1.14 min. Find out the displacement in group due to these emissions.
To solve the problem, we will analyze the decay process of uranium-238 (U-238) through alpha and beta emissions and determine the displacement in the periodic table.
1. Identify the Initial Element:
The initial element is Uranium-238, which has:
- Atomic Number (Z) = 92
- Mass Number (A) = 238
2. Alpha Particle Emission:
When an alpha particle (which has an atomic number of 2 and a mass number of 4) is emitted, the new element formed will have:
- Atomic Number after alpha emission = Z - 2 = 92 - 2 = 90
- Mass Number after alpha emission = A - 4 = 238 - 4 = 234
Thus, after the alpha emission, we have:
- New Element: 90X234
3. Beta Particle Emission:
Next, a beta particle (which has an atomic number of -1 and a mass number of 0) is emitted. This changes the atomic number of the element:
- Atomic Number after beta emission = Z + 1 = 90 + 1 = 91
- Mass Number remains the same = 234
Thus, after the beta emission, we have:
- Daughter Nucleus: 91Pa234 (Protactinium-234)
4. Determine the Displacement in Group:
Now, we need to find out the displacement in the periodic table:
- The original element (Uranium, Z = 92) belongs to Group 3 of the periodic table.
- The daughter nucleus (Protactinium, Z = 91) also belongs to Group 3.
Since both elements belong to the same group, the displacement in group is 0.
Final Answer:
The displacement in group due to these emissions is 0.
The initial element is Uranium-238, which has:
- Atomic Number (Z) = 92
- Mass Number (A) = 238
When an alpha particle (which has an atomic number of 2 and a mass number of 4) is emitted, the new element formed will have:
- Atomic Number after alpha emission = Z - 2 = 92 - 2 = 90
- Mass Number after alpha emission = A - 4 = 238 - 4 = 234
- New Element: 90X234
Next, a beta particle (which has an atomic number of -1 and a mass number of 0) is emitted. This changes the atomic number of the element:
- Atomic Number after beta emission = Z + 1 = 90 + 1 = 91
- Mass Number remains the same = 234
- Daughter Nucleus: 91Pa234 (Protactinium-234)
Now, we need to find out the displacement in the periodic table:
- The original element (Uranium, Z = 92) belongs to Group 3 of the periodic table.
- The daughter nucleus (Protactinium, Z = 91) also belongs to Group 3.
The displacement in group due to these emissions is 0.
Topper's Solved these Questions
- NUCLEAR CHEMISTRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - NUCLEAR CHEMISTRYEXERCISE - Solved Example
18 Videos
- NUCLEAR CHEMISTRYBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - NUCLEAR CHEMISTRYEXERCISE - Ex6.1 Objective
15 Videos
- NCERT BASED EXERCISEBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - NCERT BASED EXERCISEEXERCISE - Nuclear Chemistry (NCERT Exercise)
29 Videos
- ORGANIC COMPOUNDS WITH FUNCTIONAL GROUPBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ORGANIC COMPOUNDS WITH FUNCTIONAL GROUPEXERCISE - Archives Analytical And Descriptive
24 Videos
Similar Questions
.92U238 is a natural α-emitter. After α-emission the residual nucleus UX1 in turn emits a β-particle to produce another nucleus UX2. Find out the atomic number and mass number of UX1 and UX2.
View Solution.92U238 is a natural α-emitter. After α-emission the residual nucleus UX1 in turn emits a β-particle to produce another nucleus UX2. Find out the atomic number and mass number of UX1 and UX2.
View SolutionIn the disintegration of a radioactive element, α- and β-particles are evolved from the nucleus.
.0n1→.1H1+.−1e0+ Antineutrino + Energy
4.1H1→.2He4+2.+1e0+ Energy
Then, emission of these particles changes the nuclear configuration and results into a daughter nuclide. Emission of an α-particles results into a daughter element having atomic number lowered by 2 and mass number by 4, on the other hand, emission of a β-particle yields an element having atomic number raised by 1.
A radioactive element belongs to IIIB group, it emits ona α- and β-particle to form a daughter nuclide. The position of daughter nuclide will be in
View SolutionNuceli A and B convert into a stable nucleus C. Nucleus A is converted into C by emitting 2αparticels and 3β-particles. Nucleus B is converted into C by emitting one α-particle and 5β-particles. At time t=0, nuclei of A are 4N0 and nuceli of B are N0. Initially, number of nuclei of C are zero. Half-life of A (into conservation of C) is 1min and that of B is 2min. Find the time (in minutes) at which rate of disintegration of A and B are equal.
View SolutionUranium 23892U is an unstable nucleaus. It decays to Thorium 23490Th, which is again an unstable nuclei which further decays to 23491Pa. Such decay is called successive dlsntegration. Let 23892U is called as A of decay constant λ1 and 23490Th is called as B of decay constant λ2 and stable nuclei 23491Pa is named as C. Here A is called parent nucleus and B is called daughter nucleus of A. Any two adjacent nuclei may be consider parem daughter nuclei. Suppose N1, N2 and N3 are number of nuclei A, B and C respectively at time t which undergoes decay. Then we can write
Aλ2−−→Bλ2−−→C
Rate of disintegration of A=dN1dt=−λ1N1
Rate of disintegration of B=−λ2N2 and net rate of formation of B=dN2dt=λ1N1−λ2N2
Rate of formation of nuclei C is equal to dN3dt=λ2N2
If at t=0, there are N0 number of nuclei of A, where as nuclei B and C are absent in the sample answer the following questions
The graph between N1, N2 & N3 with time can be best represented by
View Solution23892U(IIIB) changes to 2349 Th by emission of α- particle . Daughter element will be in -
View SolutionUranium .23892U is an ustable nucleus. It decays to Thorium .23892Th, which is again an unstable nucleus which further decays to .23491Pa. Let .23892U be called A of decay constant λ1 and .23490Th is called as B of decay constant λ2 and stable nuclei .23491Pa be called as C. Here A is called parent nucleus and B is called daughter nucleus of A. Any two adjacent nuclei may be consider parent or daughter nuclei A,B and C respectively at time 't'.
Then we can write Aλ1−−→Bλ2−−→C
Rate of disintergration of A=dN1dt=−λ1N1
Rate of disintergration of B=dN2dt=λ1N1−λ2N2
Rate of formation of nuclei C is equal to
dN3dt=−λ2N2
If at t=0, there are N0 number of nuclei of A where as nuclei B and C are absent in the sample Answer the following questions ltbgt Numeber of the nuclei of nuclei C at time t is
View SolutionUranium .23892U is an ustable nucleus. It decays to Thorium .23892Th, which is again an unstable nucleus which further decays to .23491Pa. Let .23892U be called A of decay constant λ1 and .23490Th is called as B of decay constant λ2 and stable nuclei .23491Pa be called as C. Here A is called parent nucleus and B is called daughter nucleus of A. Any two adjacent nuclei may be consider parent or daughter nuclei A,B and C respectively at time 't'.
Then we can write Aλ1−−→Bλ2−−→C
Rate of disintergration of A=dN1dt=λ1N1
Rate of disintergration of B=dN2dt=λ1N1−λ2N2
Rate of formation of nuclei C is equal to
dN3dt=λ2N2
If at t=0, there are N0 number of nuclei of A where as nuclei B and C are absent in the sample Answer the following questions
Number of nuclei of B at any time t is
View Solution(a) Calculate the activity of one mg sample .28Sr90 whose half life period is 28 years.
(b) An experiment is performed to determine the half-life of a radioactive substance which emits one beta particle for each decay process. Observation shown that an average of 8.4β−particles are emitted each second by 2.5mg of the substance. the atomic weight of the substance is 230. calculate the half0life of the substance.
(c) Determine the quantity of .84Po210 necessary to provide a source of alpha particle of 5mCi strength (T1/2 for Po =138 day).
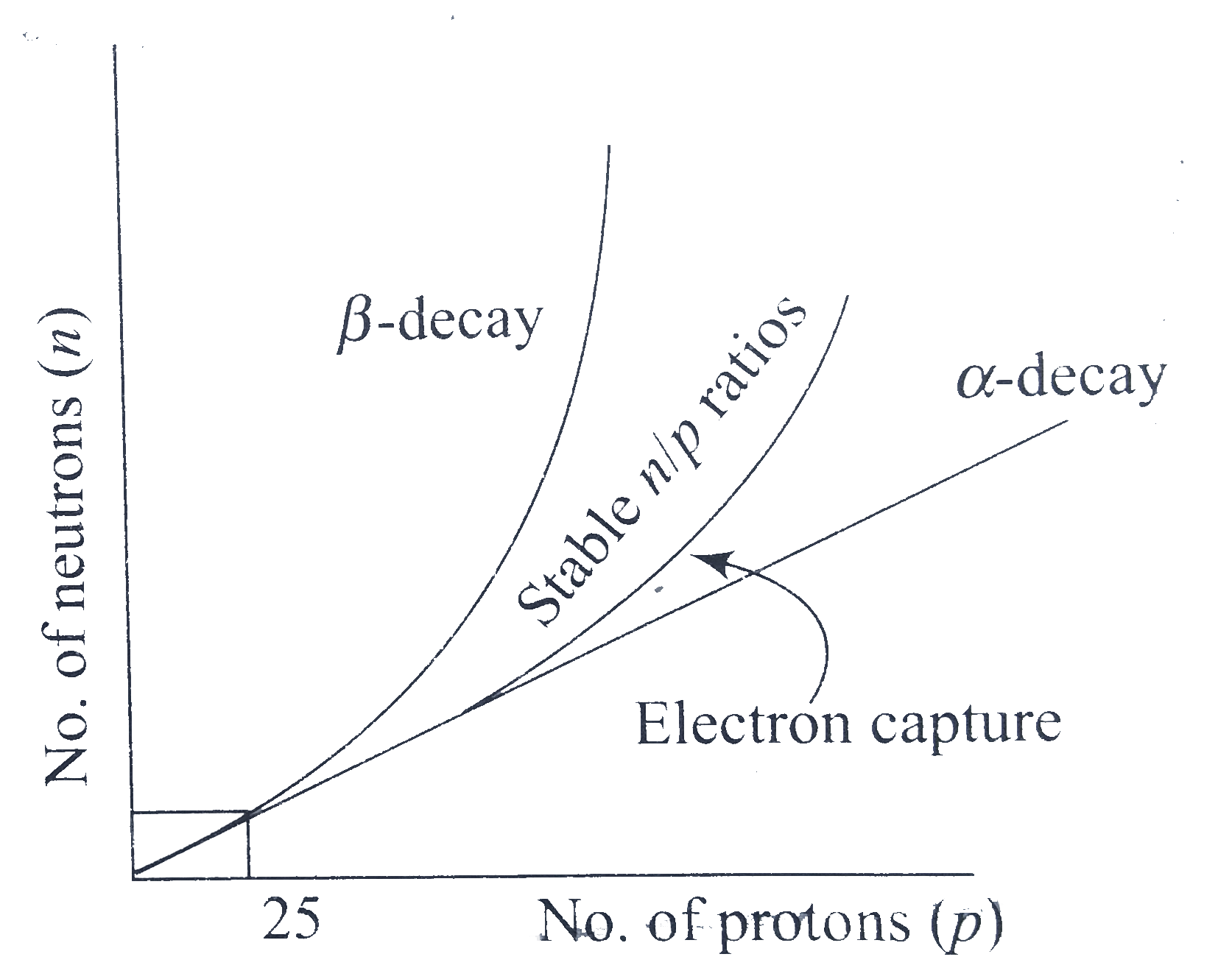
View SolutionVarious rules of thumb have seen proposed by the scientific community to expalin the mode of radioactive decay by various radioisotopes. One of the major rules is called the n/p ratio. If all the known isotopes of the elemnts are plotted on a graph of number of neutrons (n) versus number of protons (p), it is observed that all isotopes lying outside of a ''stable'' n/p ratio region are radioactive as shown fig.5.28. The graph exhibits straight line behaviour with unit slope up to p=25. Above p=25, tgose isotopes with n/p ratios lying above the stable region usually undergo beta decay. Very heavy isotopes (p>83) are unstable because of their relativley large nuclei and they undergo alpha decay. Gamma ray emission does not involve the release of a particle. It represnts a change in an atom from a higher energy level to a lower energy level.
Which of the following represents the relative penetrating power of the three types of radioactive emission in decreasing order?
View Solution
