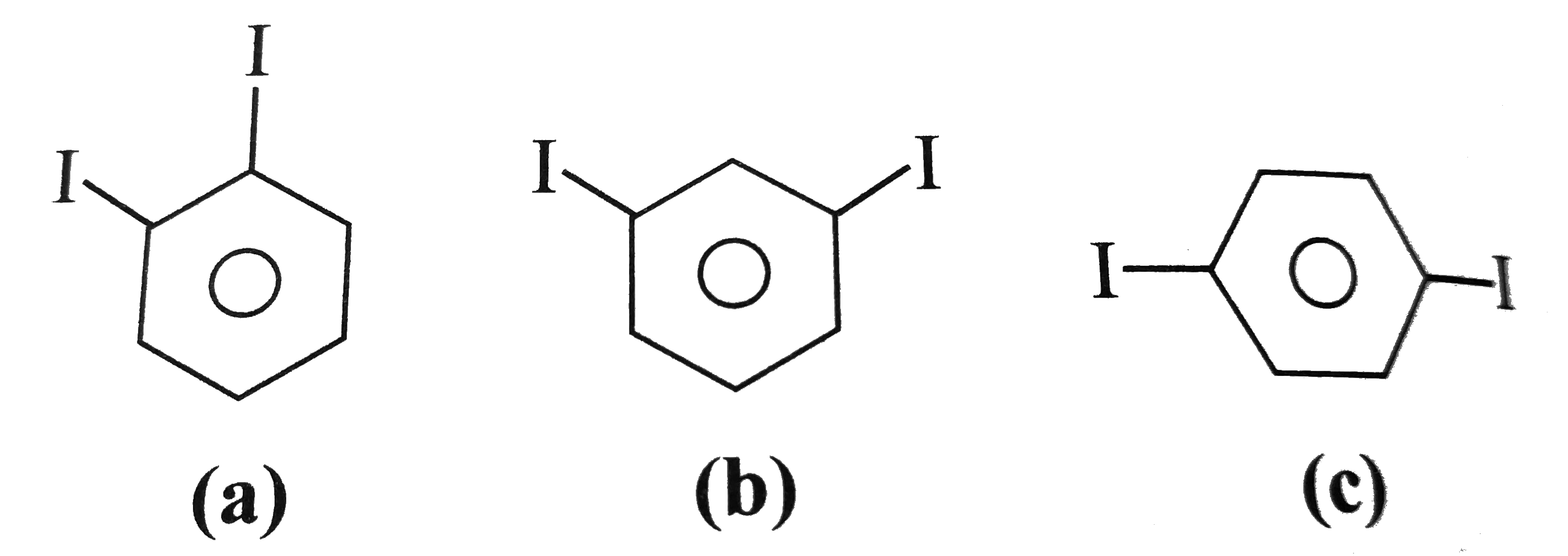
Calculate the I-I distance in each of the three isomeric diiodobenzenes Assume that the ring is a regular hexagon and that each C−I bonds lies on a line through the centre of the hexagon .
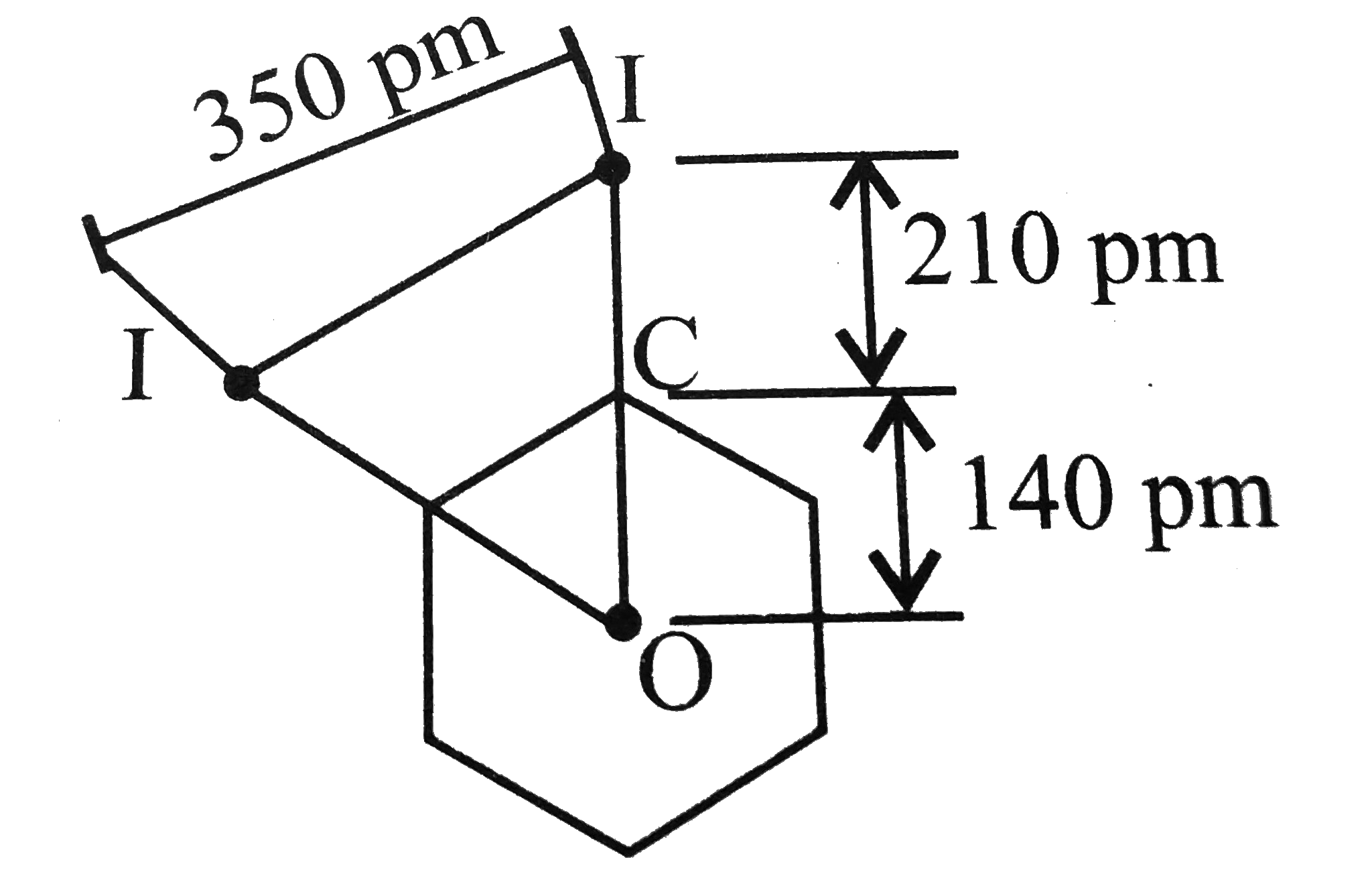
Given C−I bond length =210 pm
The distance between two adjacent C-atom (i.e C-C)
=140 pm
 .
.
The distance from the centre of the hexagon to any corner to two adjacent apics form an equilateral triangle
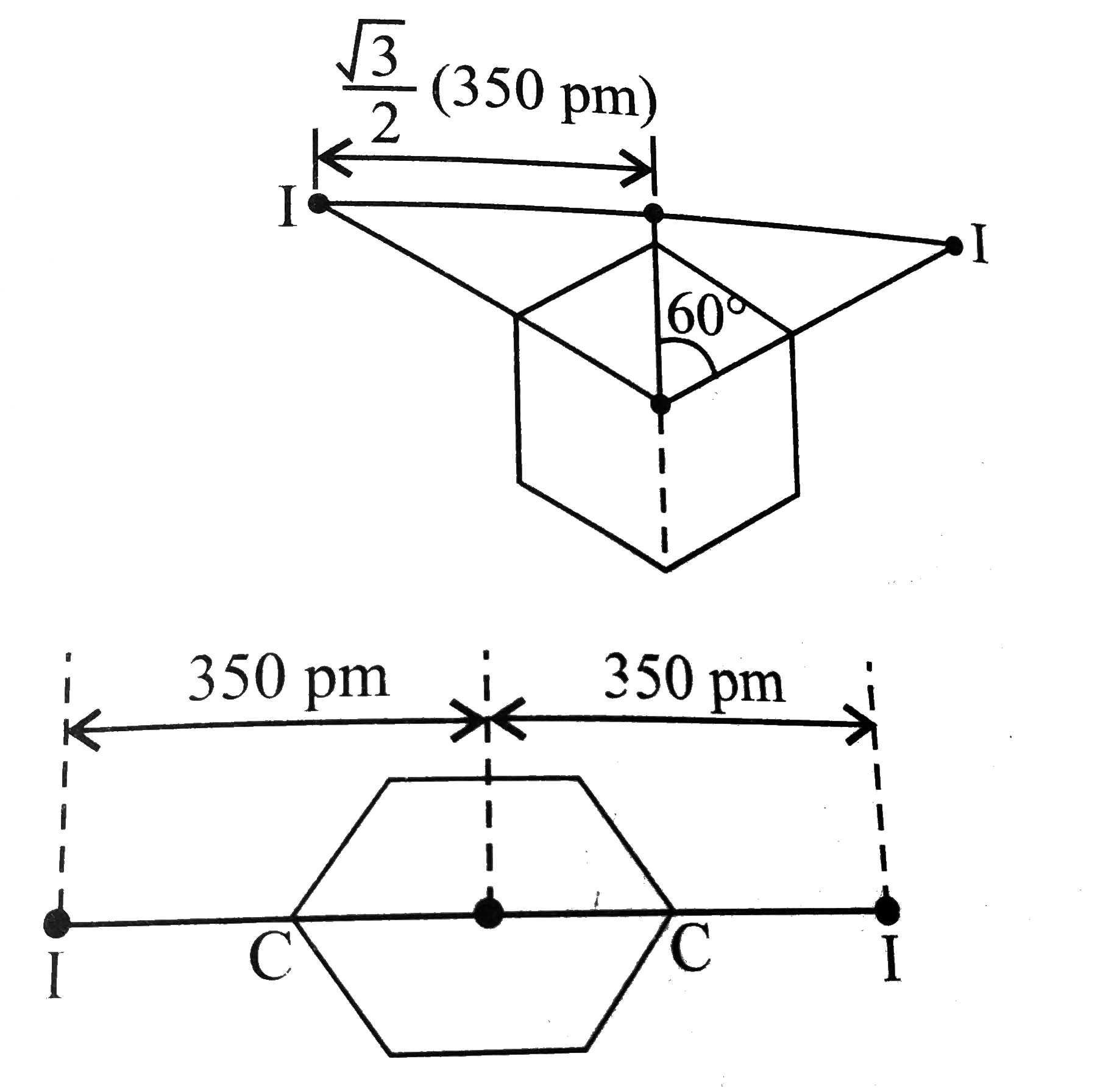
(a )The distance from the centre of the hexagon to an I atom =OC+CI=(140+210)=350 pm
(b) Half the I-I disatnce is √32 (350 pm)
Therefore I-I disatnce =√3 (350 pm)
606 pm
I-I disatnce =2 (350 pm) = 700 pm
Topper's Solved these Questions
- CHEMICAL BONDING AND MOLECULAR STRUCTUREBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL BONDING AND MOLECULAR STRUCTUREEXERCISE - Ex 2 .2 Subjective (Intermolecular Forces And H-Bonding)
7 Videos
- CHEMICAL BONDING AND MOLECULAR STRUCTUREBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL BONDING AND MOLECULAR STRUCTUREEXERCISE - Ex 2 .2 Subjective (Molecular Orbital Theory)
4 Videos
- CHEMICAL BONDING AND MOLECULAR STRUCTUREBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL BONDING AND MOLECULAR STRUCTUREEXERCISE - Archives Subjective
15 Videos
- ATOMIC STRUCTUREBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - ATOMIC STRUCTUREEXERCISE - Concept Applicationexercise(4.3)
19 Videos
- CHEMICAL EQUILIBRIUMBOOK - CENGAGE CHEMISTRY ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Subjective type
1 Videos
Similar Questions
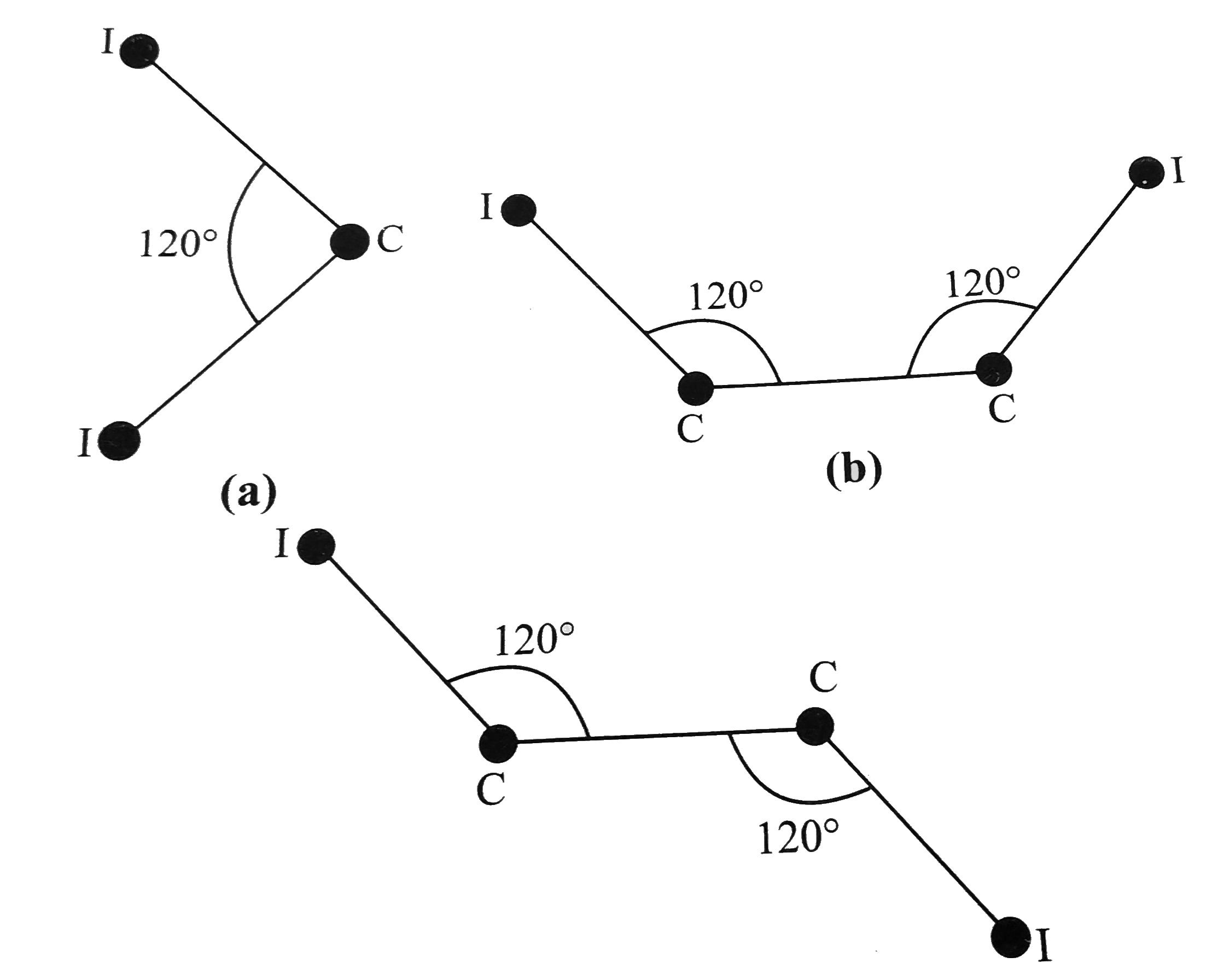
Calculate the I-I distance in each of the isomeric compounds C2H2I2 as shown below
Give Bond length of C−I⇒210 pm
Bond length of C=C⇒133 pm

 .
.
View SolutionC-Cl bond is stronger than C-I bond , because
View SolutionA circle C1 has radius 2 units and a circles C2 has radius 3 units. The distance between the centres of C1 and C2 is 7 units. If two points, one tangent to both circles and the other passing through the centre of both circles, intersect at point P which lies between the centers of C1andC2, then the distance between P and the centre of C1 is
View SolutionFig. shows three different modes of vibration of a string of length I.
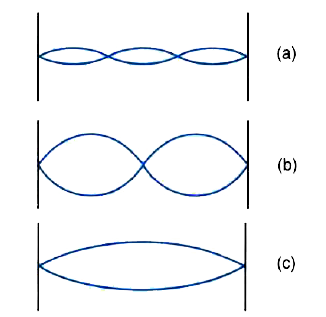
What is the ratio of frequency between (a) and (c)?
View SolutionABCDEF is a regular hexagon with centre O ). If the area of triangle OAB is 9 cm2 , find the area of: (i) the hexagon and (ii) the circle in which the hexagon is inscribed.
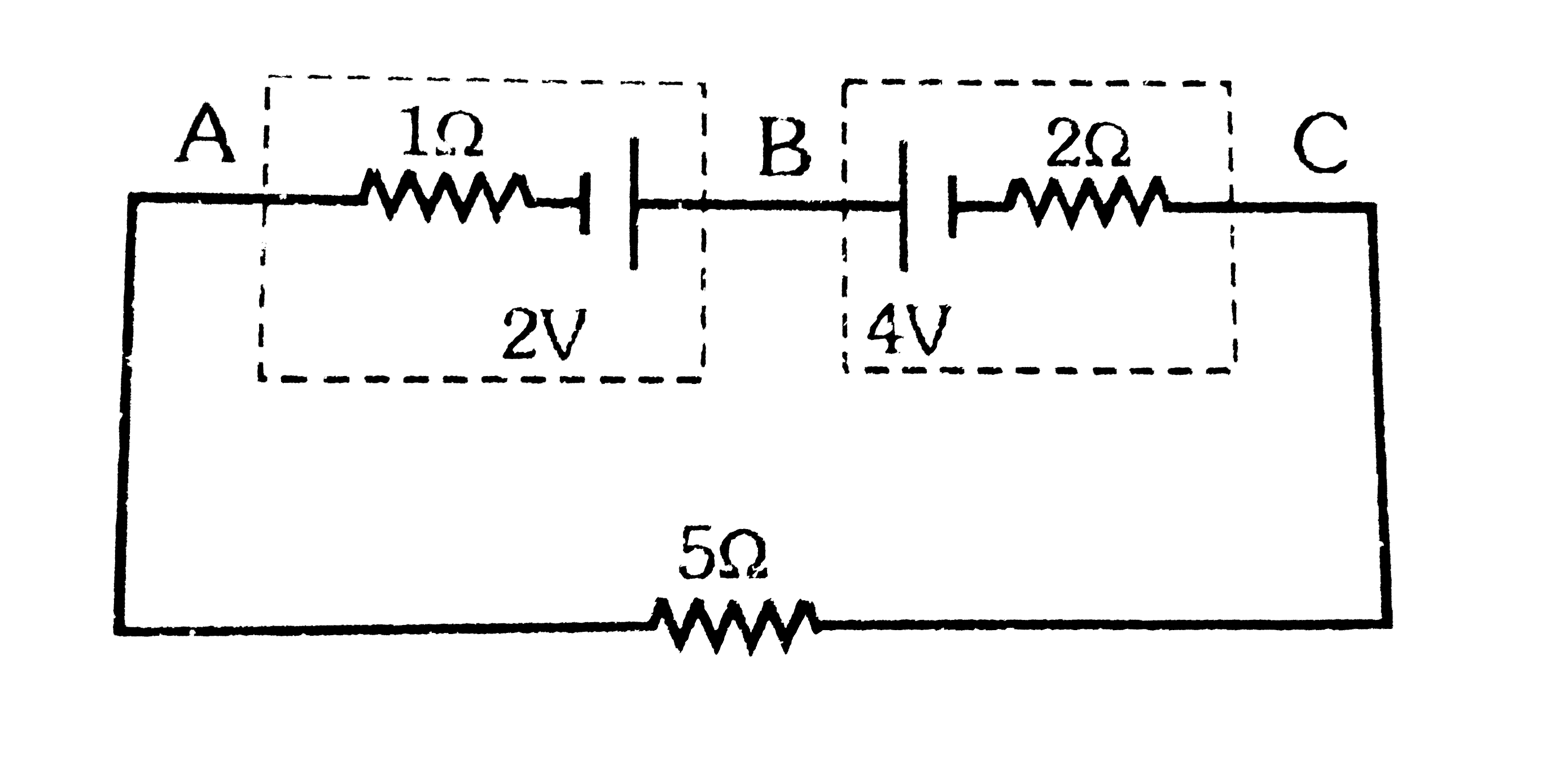
View SolutionCalculate the value of current and indicate its direction Also calculate the potential difference between the points (i) B&A (ii) A&C
View SolutionTwo points are taken at random on the given straight line segment of length a. The probability for the distance between them to exceed a given length c, where 0<c<a, is
View SolutionIf two chords AB and AC of a circle with centre O are such that the centre O lies on the bisector of ∠BAC, prove that AB=AC , i.e. the chords are equal.
View SolutionIn Fig. ABCD is a regular hexagon, which vectors are: (i) Collinear (ii) Equal (iii) Coinitial (iv) Collinear but not equal
View SolutionIf center of a regular hexagon is at the origin and one of the vertices on the Argand diagram is 1+2i , then its perimeter is 2√5 b. 6√2 c. 4√5 d. 6√5
View Solution
