A particle moves with deceleration along the circle of radius R so that at any moment of time its tangential and normal accelerations are equal in moduli . At the initial moment t=0 the speed of the particle equals v0, then the speed of the particle as a function of the distance covered s will beSolution in Bengali
v=v0e(−sR)
v=v0e(sR)
v=v0e(−Rs)
v=v0e(Rs)
The correct Answer is:A
Step by step video, text & image solution for A particle moves with deceleration along the circle of radius R so that at any moment of time its tangential and normal accelerations are equal in moduli . At the initial moment t=0 the speed of the particle equals v_0, then the speed of the particle as a function of the distance covered s will be by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
The temperature of human body is 98∘F what will be its equivalent in Centigrade scale ?
11:07View SolutionThe Young's modulus of iron and steel are 5×1010N/m2 and 2×1011N/m2 respectively. An iron wire and steel wire of same length are extended by 2 mm under the same force. If the radii of iron and steel wires are RI and RS respectively, then what will be the relation between RI and RS?
02:52View SolutionA point moves with decleration along the circle of radius R so that at any moment of time its tangential and normal accelerations are equal in moduli. At the initial moment t=0 the velocity of the point equals v_0 . Find: (a) the velocity of the point as a function of time and as a function of the distance covered s_1 , (b) the total acceleration of the point as a function of velocity and the distance covered.
04:49View SolutionA particle moves with constant speed v along a circular path of radius r and completes the circle in time T. The acceleration of the particle is
04:44View Solutiona particle is moving in a circle of radius R in such a way that at any instant the normal and the tangential component of its acceleration are equal. If its speed at t=0 is v0 then time it takes to complete the first revolution is Rαv0(1−e−βπ). Find the value of (α+β).
02:20View SolutionA particle moves with deceleration along a circle of radius R so that at any moment its tangential and normal accelerations are equal in moduli. At the initial moment t=0 the velocity of the point equals v_(0) . Find (a) the velocity of the point as a function of t and s , (b) the resultant acceleration modulus as a function of v .
02:04View SolutionA particle moves with decreasing speed along the circle of radius R so that at any moment of time its tangential and centripetal accelerations are equal in magnitude. At the initial moment , t =0 its speed is u.
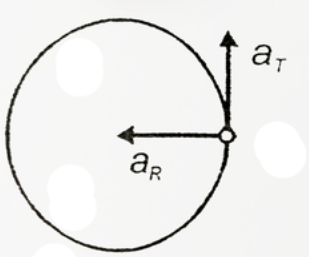
The time after which the speed of particle reduces to half of its initial value is08:05View SolutionA particle moves with decreasing speed along the circle of radius R so that at any moment of time its tangential and centripetal accelerations are equal in magnitude. At the initial moment , t =0 its speed is u.
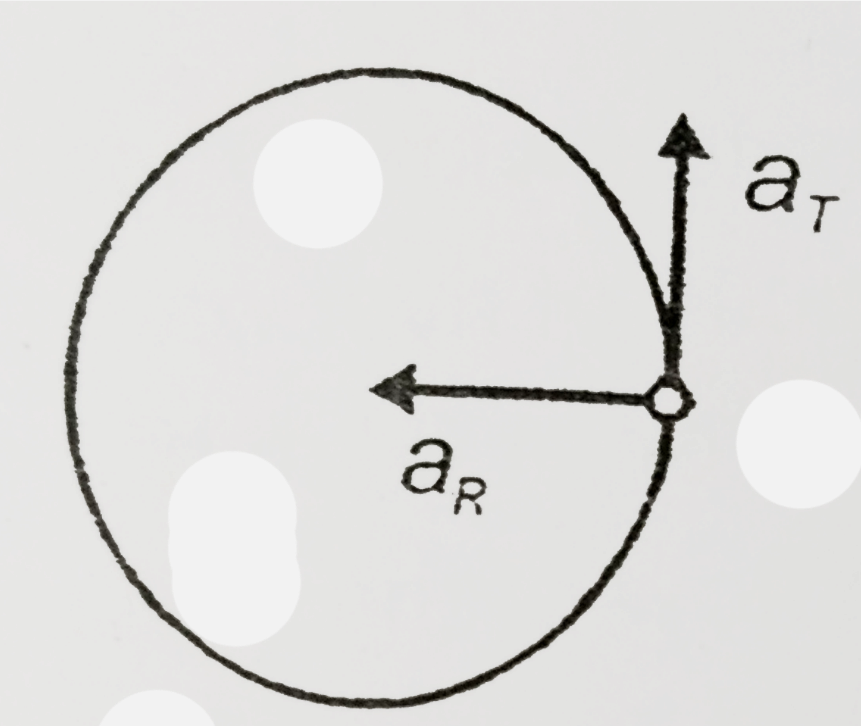
The magnitude of tangential acceleration at t=R2u is11:07View SolutionA particle is moving in a circle of radius R in such a way that at any instant the tangential retardation of the particle and the normal acceleration of the particle are equal. If its speed at t=0 is v0, the time taken to complete the first revolution is
04:39View SolutionA point moves with decleration along the circle of radius R so that at any moment of time its tangential and normal accelerations
are equal in moduli. At the initial moment t=0 the velocity of the point equals v0. Find:
(a) the velocity of the point as a function of time and as a function of the distance covered s1,
(b) the total acceleration of the point as a function of velocity and the distance covered.03:34View SolutionA particle is moving in a circle of radius R in such a way that at any instant the normal and tangential components of the acceleration are equal. If its speed at t=0 is u_(0) the time taken to complete the first revolution is :
View SolutionA particle moves with deceleration along the circle of radius R so that at any moment of time its tangential and normal acceleration are equal in moduli. At the initial moment t=0 the speed of the particle equals V0 then
The total acceleration of the particle as function of velocity and distance covered01:14View SolutionA particle is moving in a circle of radius R in such a way that at any instant the normal and tangential components of its acceleration are equal. If its speed at t=0 is Vo, the time taken to complete the first revolution is
04:45View SolutionA particle is moving on a circle of radius A .At an instant its speed and tangential acceleration are B and C respectively.Total acceleration of the particle at that instant is
00:47View SolutionA particle is moving in a circle of radius R in such a way that at any instant the normal and tangential component of the acceleration are equal. If its speed at t=0 is u0 the time taken to complete the first revolution is
View SolutionA particle moves with constant speed v along a circular path of radius r and completes the circle in time T. The acceleration of the particle is
02:15View Solution

