A point moves with decleration along the circle of radius R so that at any moment of time its tangential and normal accelerations
are equal in moduli. At the initial moment the velocity of the point equals . Find:
(a) the velocity of the point as a function of time and as a function of the distance covered ,
(b) the total acceleration of the point as a function of velocity and the distance covered.
The correct Answer is:B
Step by step video, text & image solution for A point moves with decleration along the circle of radius R so that at any moment of time its tangential and normal accelerations are equal in moduli. At the initial moment t=0 the velocity of the point equals v_0. Find: (a) the velocity of the point as a function of time and as a function of the distance covered s_1, (b) the total acceleration of the point as a function of velocity and the distance covered. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A particle moves with deceleration along a circle of radius R so that at any moment its tangential and normal accelerations are equal in moduli. At the initial moment t=0 the velocity of the point equals v0. Find (a) the velocity of the point as a function of t and s , (b) the resultant acceleration modulus as a function of v.
View SolutionA particle moves with decreasing speed along the circle of radius R so that at any moment of time its tangential and centripetal accelerations are equal in magnitude. At the initial moment , t =0 its speed is u.
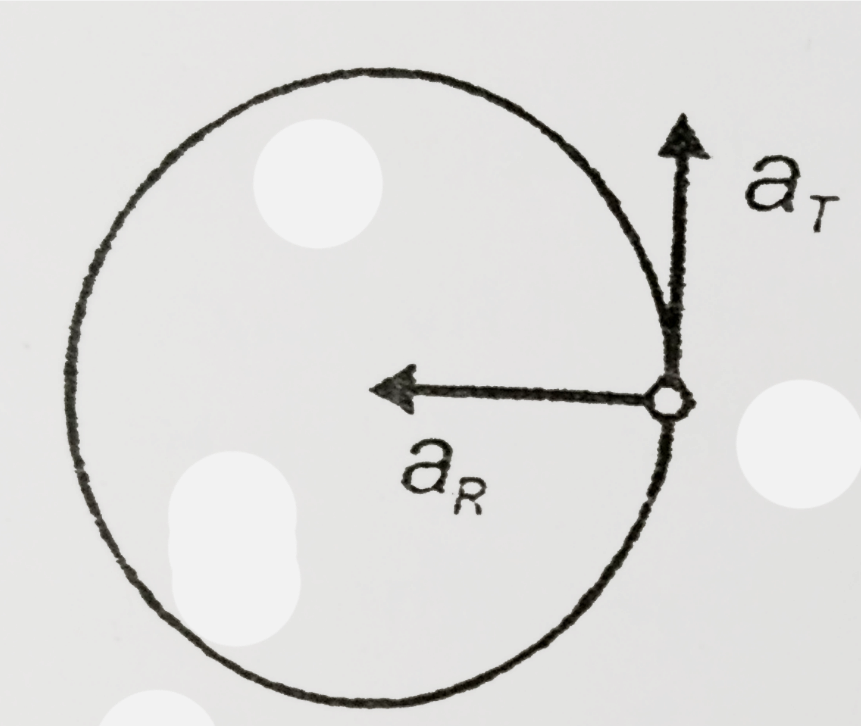
The magnitude of tangential acceleration at t=R2u is
View Solution
Knowledge Check
A particle moves with deceleration along the circle of radius R so that at any moment of time its tangential and normal acceleration are equal in moduli. At the initial moment t=0 the speed of the particle equals v0, then th speed of the particle as a function of the distance covered S will be
Av=v0e−S/RBv=v0eS/RCv=v0e−R/SDv=v0eR/SA point moves with decleration along the circle of radius R so that at any moment of time its tangential and normal accelerations
are equal in moduli. At the initial moment t=0 the velocity of the point equals v0. Find:
(a) the velocity of the point as a function of time and as a function of the distance covered s1,
(b) the total acceleration of the point as a function of velocity and the distance covered.Av=v0e−2SRBv=v0e−SRCv=v0e−SRDv=v0e−2SRA particle is moving on a circle of radius R such that at every instant the tangential and radial accelerations are equal in magnitude. If the velocity of the particle be v0 at t=0, the time for the completion of the half of the first revolution will be
AR/v0B(R/v0)(1−e−x)C(R/v0)e−xD(R/v0)(1−e−2x)
A particle moves with decreasing speed along the circle of radius R so that at any moment of time its tangential and centripetal accelerations are equal in magnitude. At the initial moment , t =0 its speed is u.
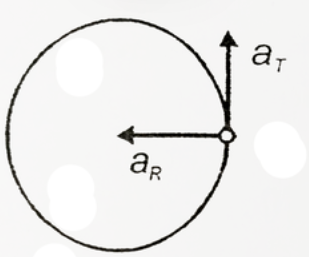
The time after which the speed of particle reduces to half of its initial value is
View SolutionA point moves rectilinearly with deceleration whose modulus depends on the velocity v of the particle as w=a√v, where a is a positive constant. At the initial moment the velocity of the point is equal to v0. What distance will it traverse before it stops? What time will it take to cover that distance?
View SolutionA particle is moving along a circular path ofradius R in such a way that at any instant magnitude of radial acceleration & tangential acceleration are equal. 1f at t = 0 velocity of particle is V0. Find the speed of the particle after time t=(R)/(2V0)
View SolutionIf a point is moving in a line so that its velocity at time t is proportional to the square of the distance covered, then its acceleration at time t varies as
View SolutionA point moves such that its displacement as a function of times is given by x2=t2+1. Its acceleration at time t is
View Solution
