Two masses of mass m each are fixed at a distance of 2d as shown in figure.

A small mass ms placed midway, when displaced slightly, starts oscillating. Then
Frequency of simple harmonic motion is given by
12π√4Gmd3
Frequency of simple harmonic motion is given by
12π√2Gmd3
Acceleration of the mass ms is given by Gmd2
Time period of vibration is 2pisqrt((GM)/((2d)^2)
The correct Answer is:B
Topper's Solved these Questions
Similar Questions
A body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is

View SolutionA plank of mass 'm' and area of cross - section A is floating as shown in figure. When slightly displaced from mean position, plank starts oscillations. Find time period of these oscillations.

View Solution
Knowledge Check
Two masses of mass m each are fixed at a separation distance of 2d. A small mass ms placed midway, when displaced slightly, starts oscillating. Then :
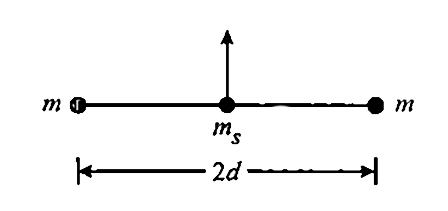 AFrequency of simple harmonic motion is given by 12π√4Gmd3BFrequency of simple harmonic motion is given by 12π√2Gmd3CAccleration of the mass ms, is given by Gmd2DTime period of vibration is 2π√GM(2d)3
AFrequency of simple harmonic motion is given by 12π√4Gmd3BFrequency of simple harmonic motion is given by 12π√2Gmd3CAccleration of the mass ms, is given by Gmd2DTime period of vibration is 2π√GM(2d)3A body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is
 A2π√m3KB2π√3m2KC2π√2m3KD2π√3Km
A2π√m3KB2π√3m2KC2π√2m3KD2π√3KmTwo electrons each are fixed at a distance '2d'. A third charge proton placed at the midpoint is displaced slightly by a distance x(x<<d) perpendicular to the line joining the two fixed charges. Proton will execute simple harmonic motion having angular frequency : (m = mass of charged particle)
A(2q2πε0md3)12B(πε0md32q2)12C(q22πε0md3)12D(2πε0md3q2)12
A plank of mass 'm' and area of cross - section A is floating as shown in figure. When slightly displaced from mean position, plank starts oscillations. Find time period of these osillations.

View SolutionTwo point masses, each equal to M, are placed a distance 2a apart. Show that a small mass m placed midway between them on the line joining them will be in equilibrium and if it is slightly displaced from this position along the line perpendicular to the line joining the masses, it will execute simple harmonic oscillations. Calculate the frequnency of these oscillations.
View SolutionA block of mass m is connected to three springs as shown in Fig. The block is displaced down slightly and left free, it starts oscillating. Find time period of oscillations.
View SolutionA body of mass 'm' hangs from three springs, each of spring constant 'k' as shown in the figure. If the mass is slightly displaced and let go, the system will oscillate with time period–
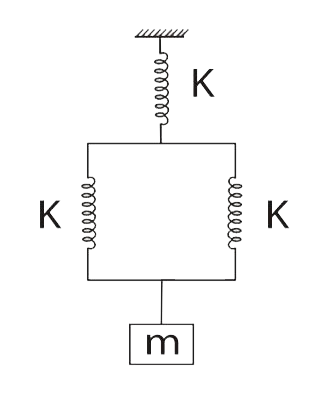
View SolutionThe frequency of the mass when it is displaced slightly is

View Solution
