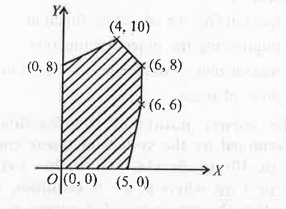
The feasible solution for a LPP is shown in the following figure. Let Z=3 x-4 y be the objective function. (Maximum value of Z+ Minimum value of Z ) is
 Solution in Kannada
Solution in Kannada
13
1
−13
−17
The correct Answer is:D
Step by step video, text & image solution for The feasible solution for a LPP is shown in the following figure. Let Z=3 x-4 y be the objective function. (Maximum value of Z+ Minimum value of Z ) is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
The inequality 4x<5 is true, when x belongs to
02:11View Solution1+3+5+....+(2n−1)=
02:45View SolutionDetermine the point of symmetry of a regular hexagon.
02:17View SolutionMatch the following Column A to Column B
 05:41View Solution
05:41View SolutionMatch the following Column A to Column B
 02:10View Solution
02:10View SolutionMatch the following Column A to Column B
 02:17View Solution
02:17View SolutionThe inequation represented by the graph given below is :
02:10View SolutionThe inequation that best describes the graph given below is _________
01:13View SolutionThe inequation that best describes the following graph is _________
01:59View SolutionIn Fig, find the value of x.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_S01_032_Q01.png" width="80%"gt01:19View SolutionThe equation of straight line shown in figure is :
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R04_E01_020_Q01.png" width="80%"gt04:30View SolutionWhat is the distance OA for the square shown in figure :- ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R05_E01_015_Q01.png" width="80%"gt
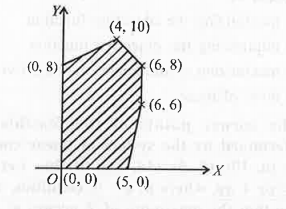
04:30View SolutionThe feasible solution for a LPP is shown in the following figure. Let Z=3 x-4 y be the objective function. Minimum of Z occurs at
 02:34View Solution
02:34View SolutionThe feasible solution for a LPP is shown in the following figure. Let Z=3 x-4 y be the objective function. Minimum of Z occurs at
 01:45View Solution
01:45View SolutionAt x=0, value of dydx is :
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R04_E01_024_Q01.png" width="80%"gt02:45View Solution

