Corner points of the feasible region determined by the system of linear constraints are (0,3),(1,1)and(3,0). Let z=px+qy, where p,q>0. Condition on p and q so that the minimum of z occurs at (3, 0) and (1, 1) is Solution in Kannada
p = 2q
p = -q/2
p = 3q
p = q
The correct Answer is:B
Step by step video, text & image solution for Corner points of the feasible region determined by the system of linear constraints are (0, 3), (1, 1) and (3, 0). Let z=px+qy, where p, q gt 0. Condition on p and q so that the minimum of z occurs at (3, 0) and (1, 1) is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
The inequality 4x<5 is true, when x belongs to
01:01View Solution1+3+5+....+(2n−1)=
03:04View SolutionThe corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5) (15, 15), (0, 20). Let Z = px + qy , where p,q>0. Then, the condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20), is
03:41View SolutionCorner points of the feasible region determined by the system of linear constraints are (0,3),(1,1)and(3,0). Let z=px+qy, where p,q>0. Condition on p and q so that the minimum of z occurs at (3, 0) and (1, 1) is
03:10View SolutionThe corner points of the feasible region determined by the system of linear constraints are as shown below:
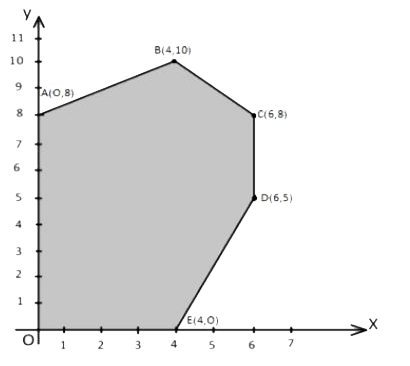
Let Z=px+qy where p,q>0 be the objective function. Find the condition on p and q so that the maximum value of Z occurs atB(4,10)andC(6,8)Also mention the number of optimal solutions in this case.02:13View SolutionThe vertices of the feasible region determined by some linear constraints are (0,2),(1,1),(3,3),(1,5). Let Z=px+qy where p,q>0. The condition on pandq so that the maximum of Z occurs at both the points (3, 3) and (1, 5) is .......
02:05View SolutionCorner points of the feasible region determined by the system of linear constraints are (0, 3), (1, 1) and (3, 0). Let Z = px + qy, where p,q>0. Condition on p and q, so that the maximum of Z occurs at (3, 0) and (1, 1) is ……….
01:35View SolutionThe corner points of the feasible region determined by some inequality are (0, 10), (5, 5), (15, 15), (0, 20). Let Z = px + qy, where p,q>0 condition on p and q so that the maximum of Z occurs at both (15, 15) and (0, 20) is …………
02:58View SolutionThe vertices of the feasible region determined by some linear constraints are (0, 2), (1, 1), (3, 3), (1, 5). Let Z = px + qy where p, q gt 0. The condition on p and q so that the maximum of Z occurs at both the points (3, 3) and (1, 5) is ……..
02:28View SolutionThe corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5) (15, 15), (0, 20). Let Z = px + qy, where p,q gt 0 . Then, the condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20), is
02:41View SolutionThe corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5) (15, 15), (0, 20). Let Z = px + qy , where p,q gt 0 . Then, the condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20), is
02:37View SolutionThe occurs point of the feasible region for an L.P.P. are (0, 3), (1, 1) and (3, 0). If objective function is Z=px+qy,p,q>0, then the condition on p and q so that the minimum of Z occurs at (3, 0) and (1, 1) is
01:28View SolutionThe corner points of the feasible region determined by the system linear constraints are (0,10), (5,5), (15,15), (0,20). Let Z = px+ qy, where p, q>0, condition on p and q so that the maximum of Z occurs at both the points (15,15) and (0,20) is
01:28View SolutionCorner points of the feasible region determined by the system of linear constraints are (0,3), (1,1) and (3,0). Let Z=px+qy, where p,q>0.
Find the condition in p and q, so that the minimum of Z occurs at (3,0) and (1,1).01:28View SolutionCorner points of the feasible region determined by the system of linear constraints are (0,3), (1,1) and (3,0). Let Z=px+qy, where p,q>0.
Find the condition in p and q, so that the minimum of Z occurs at (3,0) and (1,1).01:28View SolutionCorner points of the feasible region determined by the system of linear constraints are (0,3), (1,1) and (3,0). Let Z=px+qy, where p,q>0.
Find the condition in p and q, so that the minimum of Z occurs at (3,0) and (1,1).02:06View Solution

