The corner points of the feasible region determined by the system of linear constraints are (0,0), (0,40), (20,40), (60, 20), (60, 0). The objective function is Z = 4x + 3y. Compare the quantity in column in A and column B. Column A= Maximum of Z Column B= 325Solution in Kannada
The quantity in column B is greater
The quantity in column A is greater
The two quantities are equal
The relationship can not be determined on the basis of the information supplied
The correct Answer is:A
Step by step video, text & image solution for The corner points of the feasible region determined by the system of linear constraints are (0,0), (0,40), (20,40), (60, 20), (60, 0). The objective function is Z = 4x + 3y. Compare the quantity in column in A and column B. Column A= Maximum of Z Column B= 325 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
The inequality 4x<5 is true, when x belongs to
01:14View Solution1+3+5+....+(2n−1)=
02:18View SolutionThe corner points of the feasible region determined by the system of linear contraints are (0,0), (0,40),( 20,40),(60,20),(60,0). The objective function is Z=4x+3y. Compare the quantity in Column A and Column B.
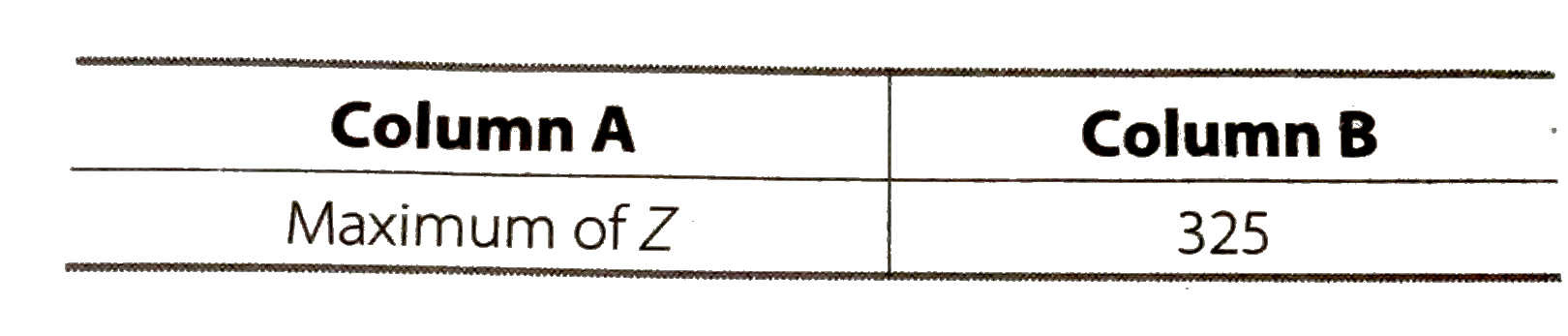03:41View SolutionLet A(0, 75), B(90, 0) , C(60, 40) and D(45, 25) be the corner points of the bounded feasible region of a LPP . If the objective function is Z=3x+4y, then Z is maximum at corner point-
03:04View SolutionThe corner points of the feasible region determined by the system of linear constraints are as shown below:
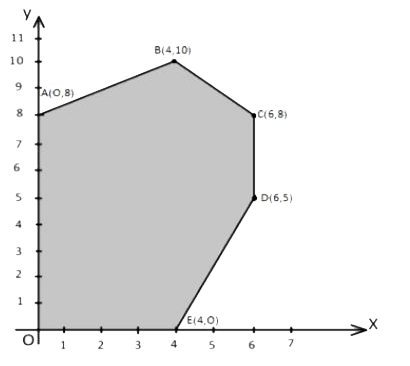
Let Z=px+qy where p,q>0 be the objective function. Find the condition on p and q so that the maximum value of Z occurs atB(4,10)andC(6,8)Also mention the number of optimal solutions in this case.01:32View SolutionThe corner points of the feasible region determined by the system of linear contraints are (0,0), (0,40),( 20,40),(60,20),(60,0). The objective function is Z=4x+3y. Compare the quantity in Column A and Column B.
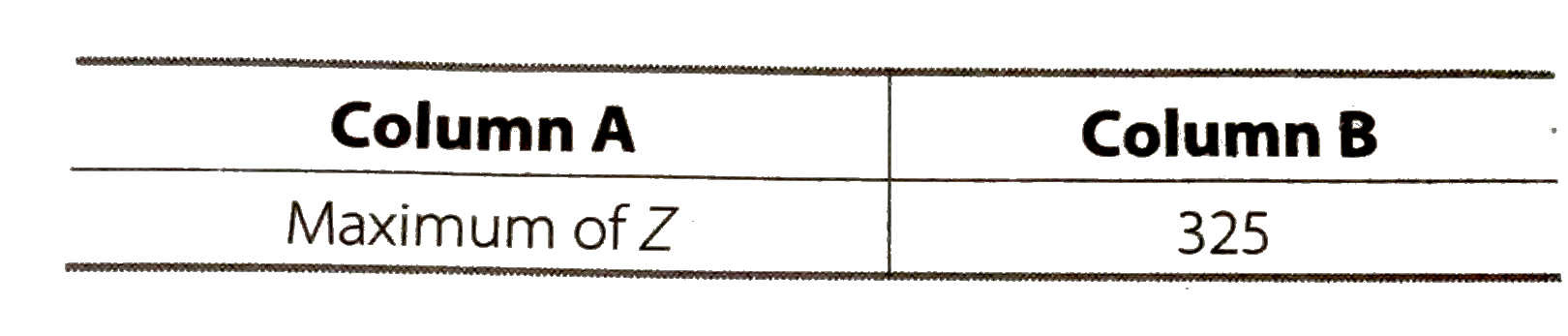02:42View SolutionThe value of objective function is maximum under linear constraints (a) At the centre of feasible region (b)At (0,0) (c)At any vertex of feasible region (d)The vertex which is maximum distance from (0,0)
02:23View Solutionव्यवरोधों के एक निकाय द्वारा निर्धारित किसी सुसंगत क्षेत्र के कोनीय बिंदु (0, 0), (0, 40), (20, 40), (60, 20), (60, 0) हैं। उद्देश्य फलन Z = 4x + 3y है। 26. स्तंभ A तथा स्तंभ B की राशियों की तुलना कीजिए।
02:58View SolutionThe corner points of the feasible region determined by the system of linear constraints are (0, 0), (0, 40), (20, 40), (60, 20), (60, 0). The objective function is z = 4x + 3y.
Compare the quantity in Column A and Column B
02:56View SolutionThe corner points of the bounded feasible region are (60, 0), (120, 0), (60, 40), (40, 20) and (20, 30). For the objective function z = 5x + 10y ………
(i) Maximum value of z.
(ii) Minimum value of z.
(iii) Maximum value of z has at ………..
(iv) Minimum value of z has at ...........01:40View SolutionThe corner points of the feasible region determined by the system of linear constraints are (0, 0), (0,40), (20,40), (60, 20), (60, 20), (60,0). The objective function is Z=4x+3 y Compare the quantity in Column A and Column B
Column AColumn BMaximum of Z32502:20View SolutionThe corner points of the feasible regon determined by the system of linear inequalities constrains are (0,0),(0,40),(20,40),(60,0). The objective function is z=4x+3y. Compare the quantity in column A and colum B.
02:39View SolutionFor an objective function Z=ax+by, where a,b>0, the corner points of the feasible region determined by a set of constraints (linear inequalities) are (0, 20), (10, 10), (30, 30) and (0, 40). The condition on a and b such that the maximum Z occurs at both the points (30, 30) and (0, 40) is:
03:23View SolutionLinear programming is a method for finding the optimal values (maximum or minimum) of quantities subject to the constraints when relationship is expressed as linear equations or inequations. Based on the above information, answer the following questions. The corner points of the feasible region determined by the system of linear constraints are (0, 0), (0.40),(20,40), (60, 20), (60, 0) The objective function is 2-4x+3y Compare the quantity in Column A and Column B
02:05View SolutionFor an objective function Z = ax + by, where a,b>0, the corner points of the feasible region determined by a set of constraints (linear inequalities) are (0, 20). (10, 10), (30, 30) and (0, 40). The condition on a and b such that the maximum z occurs at both the points (30, 30) and (0, 40) is:
01:59View Solution