A particle of mass is placed at the lowest point of a smooth parabola having the equation (x, y in m). Here is the vertical height. If it is displaced slightly and it.is constrained to move along the parabola, find the angular frequency (in rad/s) of small oscillations.
The correct Answer is:20
Topper's Solved these Questions
Similar Questions
A particle of mass 5×10−5kg is placed at the lowest point of a smooth parabola having the equation 20t2=y (x, y in m). Here y is the vertical height. If it is displaced slightly and it.is constrained to move along the parabola, find the angular frequency (in rad/s) of small oscillations.
View SolutionA point mass m is displaced slightly from point O and released. It is constrained to move along parabolic path having equation x2=ky then its angular frequency of oscillation is :
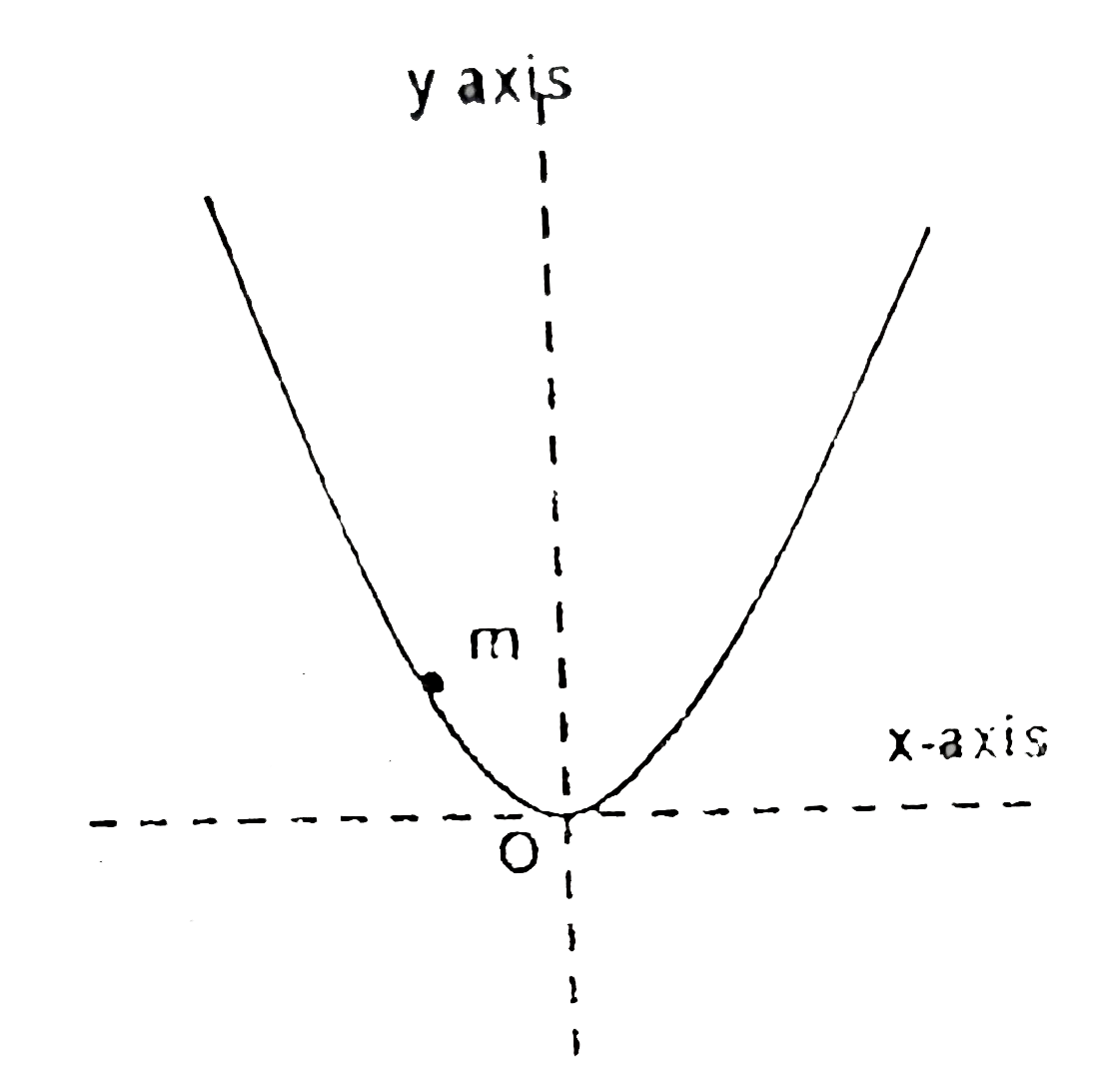
View Solution
Knowledge Check
A point mass m is displaced slightly from point O and released. It is constrained to move along parabolic path having equation x2=ky then its angular frequency of oscillation is :
 A√g2kB√2gkC√gkD√3g2k
A√g2kB√2gkC√gkD√3g2kA particle is placed at the lowest point of a smooth wire frame in the shape of a parabola, lying in the vertical xy-plane having equatioin x2=5y(x,y are in meter). After slight displacement, the particle is set free. Find angular frequency of osciallation (in rad/sec) (Take g=10 m/s2)
A2 rad/sB4 rad/sC6 rad/sD8 rad/s
A particle is placed at the lowest point of a smooth wire frame in the shape of a parabola, lying in the vertical xy-plane having equatioin x2=5y(x,y are in meter). After slight displacement, the particle is set free. Find angular frequency of osciallation (in rad/sec) (Take g=10 m/s2)
View SolutionFind the equation of tangents of the parabola y2=12x, which passes through the point (2, 5).
View SolutionFind the equation of the tangent with slopes 5 to the parabola y2=20x, also find the coordinates of the point of contact of the tangent to the parabola.
View SolutionFind the equation of tangents of the parabola y2=12x, which passes through the point (2, 5).
View SolutionFind the equation of tangents of the parabola y2=12x, which passes through the point (2, 5).
View SolutionFind the locus of midpoint of family of chords λx+y=5(λ is parameter) of the parabola x2=20y
View Solution
