Diagonals of rhombus ABCD intersect each other at point O. Prove that :
OA2+OC2=2AD2−BD22
Step by step video & image solution for Diagonals of rhombus ABCD intersect each other at point O. Prove that : " "OA^(2)+OC^(2)=2AD^(2)-(BD^(2))/2 by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
ABCD is a trapezium such that AB||CD. Its diagonals AC and BC intersect each other at O. Prove that AOOC=BOOD
View SolutionIn a trapezium ABCD, side AB is parallel to side DC, and the diagonals AC and BD intersect each other at point P. Prove that :
PA×PD=PB×PC.
View SolutionThe diagonals of a quadrilateral ABCD intersect each other at the point O such that AOBO=CODO. Show that ABCD is a trapezium.
View SolutionProve that :The diagonals of a rhombus bisect each other at right angle.
View Solutionif diagonals of a parallelogram bisect each other,prove that its a rhombus
View SolutionABCD is a trapezium in which AB||DC and its diagonals intersect each other at the point O. Show that AOBO=CODO.
View SolutionIn a trapezium ABCD, side AB is parallel to side DC, and the diagonals AC and BD intersect each other at point P. Prove that :
ΔAPB is similar to ΔCPD.
View SolutionIn figure , if Ab||DC and AC, PQ interrest each other at the point 0. Prove that OA.CQ=OC.AP.

View SolutionIn the adjoining figure, ABCD is a quadrilateral in which AD∣∣BC. AC and BD intersect each other at point 'O'. Prove that:
area of ΔCOD= area of ΔABO
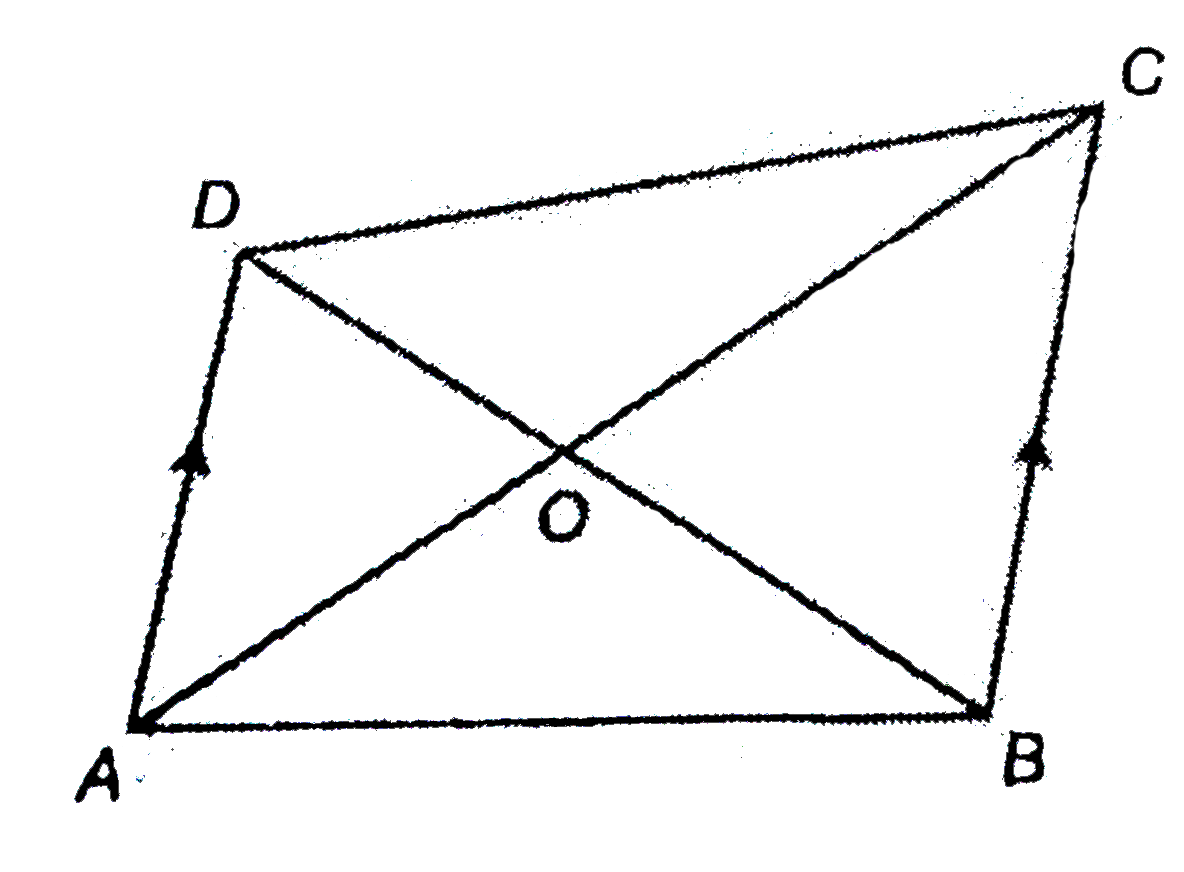
View SolutionIn quadrilateral ABCD, the diagonals AC and BD intersect each other at point O.
If AO = 2CO and BO = 2DO, show that:
OA×OD=OB×OC.
View Solution
