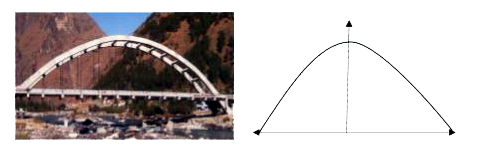
The bridge connects two hills 100 feet apart. The arch on the bridge is in a parabolic form. The highest point on the bridge is 10 feet above the road at the middle of the bridge as seen in the figure.
Based on the information given above, answer the following questions:
The integrand of the integral ∫50−50x2dx is ________ function.
Even
Odd
Neither odd nor even
None
The correct Answer is:A
Step by step video & image solution for The bridge connects two hills 100 feet apart. The arch on the bridge is in a parabolic form. The highest point on the bridge is 10 feet above the road at the middle of the bridge as seen in the figure. Based on the information given above, answer the following questions: The integrand of the integral int_(-50)^(50)x^(2)dx is ________ function. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUESTION BANK 2021BOOK - CBSE MODEL PAPERCHAPTER - QUESTION BANK 2021EXERCISE - QUESTIONS
9 Videos
- Additional Practice QuestionsBOOK - CBSE MODEL PAPERCHAPTER - Additional Practice QuestionsEXERCISE - Question
47 Videos
- SAMPLE QUESTION PAPER ( MATHEMATICS )BOOK - CBSE MODEL PAPERCHAPTER - SAMPLE QUESTION PAPER ( MATHEMATICS )EXERCISE - QUESTION
60 Videos
Similar Questions

The bridge connects two hills 100 feet apart. The arch on the bridge is in a parabolic form. The highest point on the bridge is 10 feet above the road at the middle of the bridge as seen in the figure.
Based on the information given above, answer the following questions:
The value of the integral ∫50−50x2250dx is
View Solution
The bridge connects two hills 100 feet apart. The arch on the bridge is in a parabolic form. The highest point on the bridge is 10 feet above the road at the middle of the bridge as seen in the figure.
Based on the information given above, answer the following questions:
The equation of the parabola designed on the bridge can be
View Solution
The bridge connects two hills 100 feet apart. The arch on the bridge is in a parabolic form. The highest point on the bridge is 10 feet above the road at the middle of the bridge as seen in the figure.
Based on the information given above, answer the following questions:
The area formed between x2=250y, y-axis , y = 2 and y = 4 is
View Solution
The bridge connects two hills 100 feet apart. The arch on the bridge is in a parabolic form. The highest point on the bridge is 10 feet above the road at the middle of the bridge as seen in the figure.
Based on the information given above, answer the following questions:
The area formed by the curve x2=250y, x-axis , y = 0 and y = 10 is
View SolutionFor the origin O, given two points A and B such that ∠AOB=90∘ on a parabola y=x2 .The line joining A and B has slope 2.On the basis of above information,answer the following questions: The area of ΔOAB is -
View SolutionFor the origin O given two points A and B such that ∠AOB=90∘ on a parabola y=x2 .The line joining A and B has slope 2. on the basis of above information answer the following questions: The equation of line AB is
View SolutionFor the origin O, given two points A and B such that ∠AOB=90∘ on a parabola y=x2. The line joining A and B has slope 2. On the basis of above information, answer the following question: The equation of line AB is
View SolutionAmit is planning to buy a house and the layout is given below. The design and the measurement has been made such that areas of two bedrooms and kitchen together is 95 sq.m.
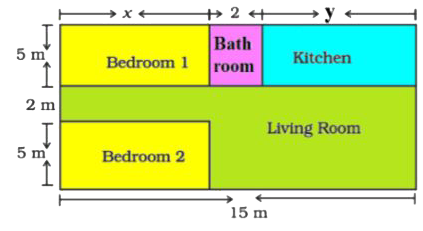
Based on the above information, answer the following questions:
Find the cost of laying tiles in kitchen at the rate of Rs. 50 per sq.m
View SolutionI here is a parabolic shaped bridge across the river of width 10 meter.The highest point of the bridge is 4 meter above the level of bank.A car of mass 72kg is crossing the bridge at a constant speed of 5m/s . Find the force (in Newton) exerted on the bridge by car when it is at the highest point P of the bridge.(takeg=10ms2)
View SolutionManjit wants to donate a rectangular plot of land for a school in his village. When he was asked to give dimensions of the plot, he told that if its length is decreased by 50 m and breadth is increased by 50m, then its area will remain same, but if length is decreased by 10m and breadth is decreased by 20m, then its area will decrease by 5300m2
Based on the information given above, answer the following questions:

The equations in terms of X and Y are
View Solution
