
The bridge connects two hills 100 feet apart. The arch on the bridge is in a parabolic form. The highest point on the bridge is 10 feet above the road at the middle of the bridge as seen in the figure.
Based on the information given above, answer the following questions:
The area formed between x2=250y, y-axis , y = 2 and y = 4 is
10003
0
1000√23
none of these
The correct Answer is:D
Step by step video & image solution for The bridge connects two hills 100 feet apart. The arch on the bridge is in a parabolic form. The highest point on the bridge is 10 feet above the road at the middle of the bridge as seen in the figure. Based on the information given above, answer the following questions: The area formed between x^(2)=250y, y-axis , y = 2 and y = 4 is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUESTION BANK 2021BOOK - CBSE MODEL PAPERCHAPTER - QUESTION BANK 2021EXERCISE - QUESTIONS
9 Videos
- Additional Practice QuestionsBOOK - CBSE MODEL PAPERCHAPTER - Additional Practice QuestionsEXERCISE - Question
47 Videos
- SAMPLE QUESTION PAPER ( MATHEMATICS )BOOK - CBSE MODEL PAPERCHAPTER - SAMPLE QUESTION PAPER ( MATHEMATICS )EXERCISE - QUESTION
60 Videos
Similar Questions

The bridge connects two hills 100 feet apart. The arch on the bridge is in a parabolic form. The highest point on the bridge is 10 feet above the road at the middle of the bridge as seen in the figure.
Based on the information given above, answer the following questions:
The area formed by the curve x2=250y, x-axis , y = 0 and y = 10 is
View Solution
The bridge connects two hills 100 feet apart. The arch on the bridge is in a parabolic form. The highest point on the bridge is 10 feet above the road at the middle of the bridge as seen in the figure.
Based on the information given above, answer the following questions:
The value of the integral ∫50−50x2250dx is
View Solution
Knowledge Check
The area included between x2+y2=4xandy2=x above x-axis is
A43(3π−8)B23(8+3π)C13(4+3π)D5√32+2π3

The bridge connects two hills 100 feet apart. The arch on the bridge is in a parabolic form. The highest point on the bridge is 10 feet above the road at the middle of the bridge as seen in the figure.
Based on the information given above, answer the following questions:
The equation of the parabola designed on the bridge can be
View Solution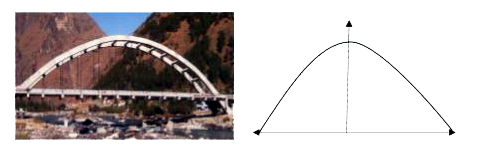
The bridge connects two hills 100 feet apart. The arch on the bridge is in a parabolic form. The highest point on the bridge is 10 feet above the road at the middle of the bridge as seen in the figure.
Based on the information given above, answer the following questions:
The integrand of the integral ∫50−50x2dx is ________ function.
View SolutionFor the origin O, given two points A and B such that ∠AOB=90∘ on a parabola y=x2 .The line joining A and B has slope 2.On the basis of above information,answer the following questions: The area of ΔOAB is -
View SolutionFor the origin O given two points A and B such that ∠AOB=90∘ on a parabola y=x2 .The line joining A and B has slope 2. on the basis of above information answer the following questions: The equation of line AB is
View SolutionGiven below two equations are there. Based on the given information, you have to determine the relation between x and y.
2x2−22x+48=0
y2−20y+96=0
View SolutionFor the origin O, given two points A and B such that ∠AOB=90∘ on a parabola y=x2. The line joining A and B has slope 2. On the basis of above information, answer the following question: The equation of line AB is
View SolutionLet (x,y,z)=sin2x+sin2y+sin2z.On the basis of above information, answer the following questions :If x+y+z=2π, then f(x,y,z)=
View Solution
