Two particles A and B have the same mass m. A is moving along X-axis with a speed of 5ms−1 and B is at rest. After undergoing a perfectly elastic collision with B, particle A gets scattered through an angle of 60∘. What is the direction of B, and the speeds of A and B, after the collision ?
To solve the problem, we will follow these steps:
Step 1: Understand the Initial Conditions
- Particle A has a mass m and is moving along the X-axis with a speed of u1=5m/s.
- Particle B has the same mass m and is initially at rest, so u2=0.
- After the collision, particle A is scattered at an angle θ=60∘.
Step 2: Apply the Conservation of Momentum
In a perfectly elastic collision, both momentum and kinetic energy are conserved.
Momentum Conservation in X-direction:
The initial momentum in the x-direction is:
Pinitial=mu1+mu2=m⋅5+m⋅0=5m
After the collision, the momentum in the x-direction is:
Pfinal=mv1cos(60∘)+mv2cos(ϕ)
Where:
- v1 is the speed of particle A after the collision.
- v2 is the speed of particle B after the collision.
- ϕ is the angle at which particle B moves after the collision.
Setting the initial momentum equal to the final momentum gives:
5m=mv1cos(60∘)+mv2cos(ϕ)
Dividing through by m (since m≠0):
5=v1⋅12+v2cos(ϕ)(1)
Momentum Conservation in Y-direction:
The initial momentum in the y-direction is zero since both particles are moving along the x-axis. Therefore:
0=mv1sin(60∘)−mv2sin(ϕ)
This simplifies to:
v1sin(60∘)=v2sin(ϕ)(2)
Step 3: Use the Relationship Between Angles
In a perfectly elastic collision, the angles of scattering and recoil are related by:
θ+ϕ=90∘
Thus:
ϕ=90∘−θ=90∘−60∘=30∘
Step 4: Substitute the Angle into the Equations
Now substituting ϕ=30∘ into equations (1) and (2):
From equation (1):
5=v1⋅12+v2⋅cos(30∘)
Using cos(30∘)=√32:
5=v12+v2⋅√32(3)
From equation (2):
v1⋅sin(60∘)=v2⋅sin(30∘)
Using sin(60∘)=√32 and sin(30∘)=12:
v1⋅√32=v2⋅12
This simplifies to:
v2=√3v1(4)
Step 5: Substitute Equation (4) into Equation (3)
Substituting v2 from equation (4) into equation (3):
5=v12+√3v1⋅√32
This simplifies to:
5=v12+3v12=2v1
Thus:
v1=52=2.5m/s
Step 6: Find v2
Using equation (4):
v2=√3v1=√3⋅2.5=5√32≈4.33m/s
Final Results
- The speed of particle A after the collision is v1=2.5m/s.
- The speed of particle B after the collision is v2≈4.33m/s.
- The angle of recoil for particle B is ϕ=30∘.
- Particle A has a mass m and is moving along the X-axis with a speed of u1=5m/s.
- Particle B has the same mass m and is initially at rest, so u2=0.
- After the collision, particle A is scattered at an angle θ=60∘.
In a perfectly elastic collision, both momentum and kinetic energy are conserved.
The initial momentum in the x-direction is:
Pinitial=mu1+mu2=m⋅5+m⋅0=5m
After the collision, the momentum in the x-direction is:
Pfinal=mv1cos(60∘)+mv2cos(ϕ)
Where:
- v1 is the speed of particle A after the collision.
- v2 is the speed of particle B after the collision.
- ϕ is the angle at which particle B moves after the collision.
5m=mv1cos(60∘)+mv2cos(ϕ)
Dividing through by m (since m≠0):
5=v1⋅12+v2cos(ϕ)(1)
The initial momentum in the y-direction is zero since both particles are moving along the x-axis. Therefore:
0=mv1sin(60∘)−mv2sin(ϕ)
This simplifies to:
v1sin(60∘)=v2sin(ϕ)(2)
In a perfectly elastic collision, the angles of scattering and recoil are related by:
θ+ϕ=90∘
Thus:
ϕ=90∘−θ=90∘−60∘=30∘
Now substituting ϕ=30∘ into equations (1) and (2):
5=v1⋅12+v2⋅cos(30∘)
Using cos(30∘)=√32:
5=v12+v2⋅√32(3)
v1⋅sin(60∘)=v2⋅sin(30∘)
Using sin(60∘)=√32 and sin(30∘)=12:
v1⋅√32=v2⋅12
This simplifies to:
v2=√3v1(4)
Substituting v2 from equation (4) into equation (3):
5=v12+√3v1⋅√32
This simplifies to:
5=v12+3v12=2v1
Thus:
v1=52=2.5m/s
Using equation (4):
v2=√3v1=√3⋅2.5=5√32≈4.33m/s
- The speed of particle A after the collision is v1=2.5m/s.
- The speed of particle B after the collision is v2≈4.33m/s.
- The angle of recoil for particle B is ϕ=30∘.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - IILUSTRATION2videos
WORK, ENERGY AND POWER
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - TRY YOURSELF95videos
WORK, ENERGY AND POWER
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))12videos
WAVES
Similar Questions
Particle A makes a perfectly elastic collision with anther particle B at rest. They fly apart in opposite direction with equal speeds. If the masses are mA&mB respectively, then
View SolutionParticle A makes a perfectly elastic collision with anther particle B at rest. They fly apart in opposite direction with equal speeds. If the masses are mA&mB respectively, then
View Solution
Knowledge Check
- Question 1 - Select One
A sphere P of mass m and velocity vi undergoes an oblique and perfectly elastic collision with an identical sphere Q initially at rest. The angle θ between the velocities of the spheres after the collision shall be
A0B45∘C90∘D180∘ - Question 2 - Select One
When two spheres of equal masses undergo glancing elastic collision with one of them at rest after collision they will move
Aopposite to one anotherBin the same directionCtogetherDat right angle to each other
Two particles A and B of mass 3kg and 2kg moving with speed 10m/s and 5m/s as shown in figure.
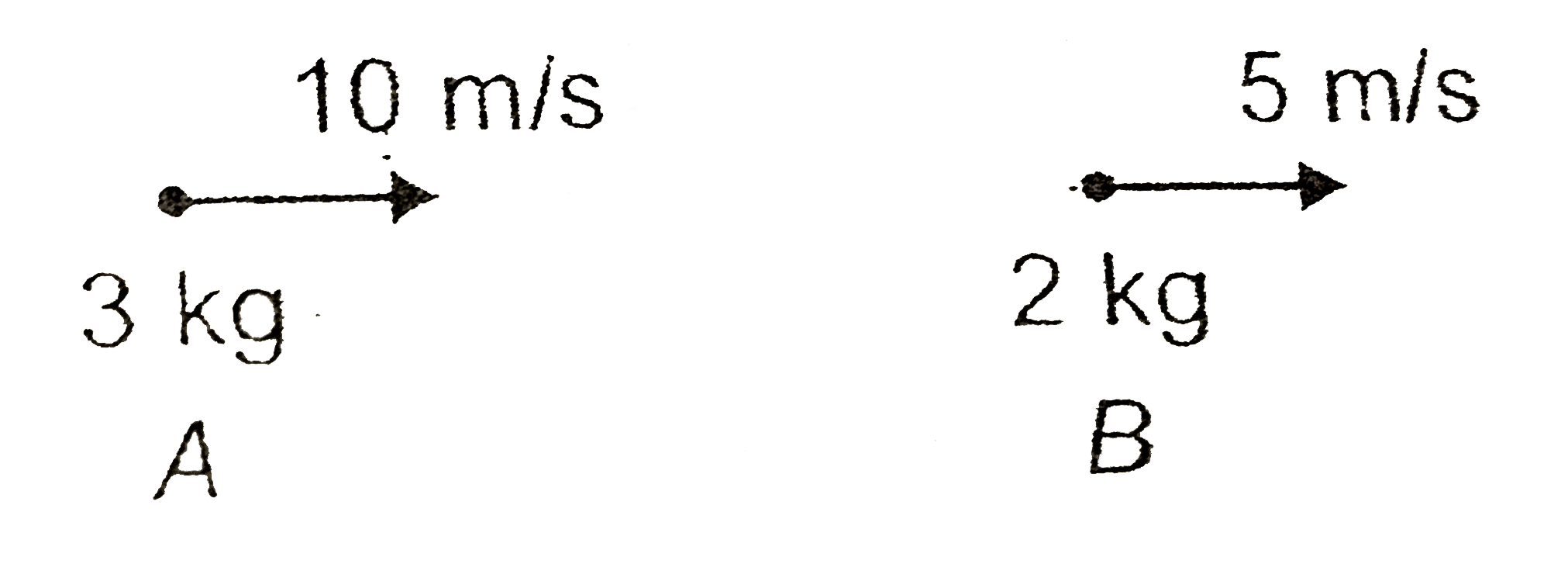
Find the maximum momentum that particle B can have after collision with AView SolutionTwo particles A and B of mass 3kg and 2kg moving with speed 10m/s and 5m/s as shown in figure.
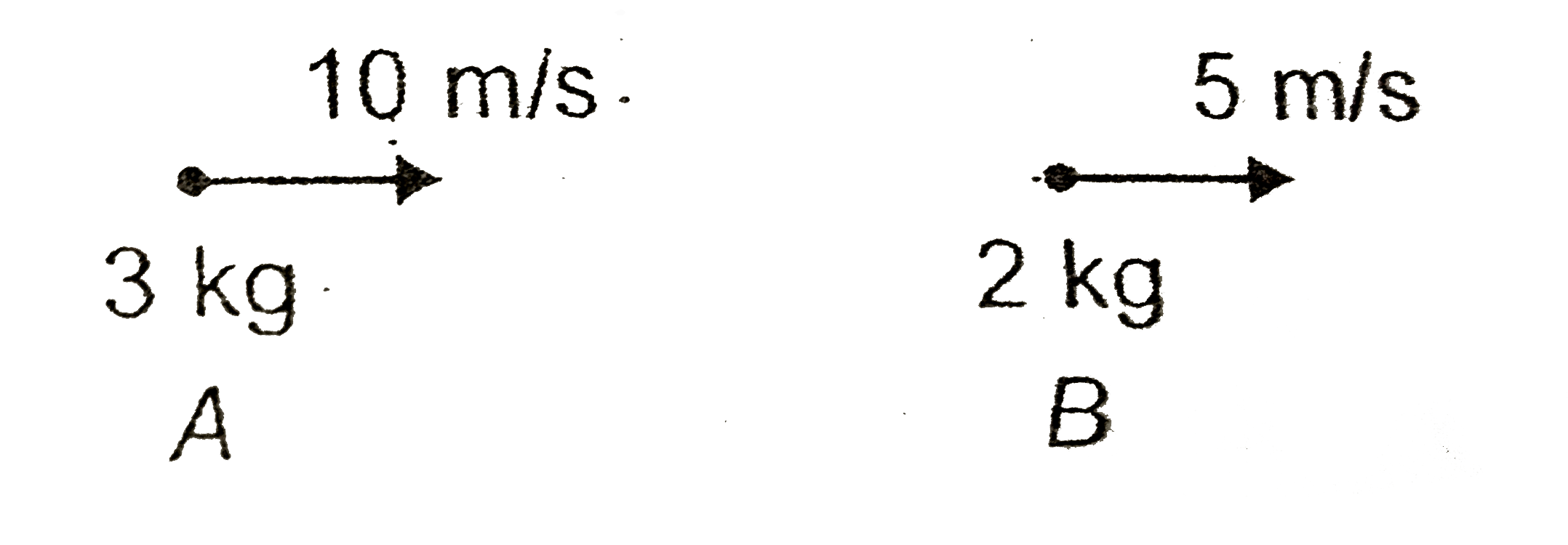
Find the maximum momentum that particles A can have after collision with B.View SolutionA ball moving with a speed of 9ms−1 strikes an identical stationary ball such that after the collision the direction of each ball makes an angle of 30∘ with the original line of motion. The speeds of two balls after the collision is
View SolutionA moving particle of mass m makes a head-on perfectly inelastic collision with a particle of mas 2m which is initially at rest. Find the fractional loss in energy of the colliding partic le after collision.
View SolutionTwo identical balls moving in opposite directions with speed 20 m/s and 25 m/s undergo head on perfectly inelastic collision. The speed of combined mass after collision is
View SolutionOn a friction surface a block a mass M moving at speed v collides elastic with another block of same mass M which is initially at rest . After collision the first block moves at an angle θ to its initial direction and has a speed v3. The second block's speed after the collision is
View Solution

