Two identical balls moving in opposite directions with speed 20 m/s and 25 m/s undergo head on perfectly inelastic collision. The speed of combined mass after collision is
20 m/s
22.5 m/s
25 m/s
2.5 m/s
The correct Answer is:D
To solve the problem of two identical balls undergoing a perfectly inelastic collision, we will use the principle of conservation of momentum. Here’s a step-by-step solution:
Step 1: Understand the scenario
We have two identical balls moving towards each other. One ball is moving at a speed of 20 m/s to the right (let's consider this as positive direction), and the other ball is moving at a speed of 25 m/s to the left (which we will consider as negative direction).
Step 2: Define the masses and velocities
Let the mass of each ball be m.
- Velocity of the first ball, v1=+20m/s
- Velocity of the second ball, v2=−25m/s
Step 3: Apply the conservation of momentum
In a perfectly inelastic collision, the two objects stick together after the collision. According to the conservation of momentum:
Initial momentum=Final momentum
The initial momentum before the collision is given by:
pinitial=m⋅v1+m⋅v2=m⋅20+m⋅(−25)
pinitial=m(20−25)=m(−5)
Step 4: Calculate the final momentum
After the collision, both balls move together with a common velocity vf. The final momentum is:
pfinal=(m+m)⋅vf=2m⋅vf
Step 5: Set the initial momentum equal to the final momentum
Setting the initial momentum equal to the final momentum gives:
m(−5)=2m⋅vf
We can cancel m from both sides (assuming m≠0):
−5=2vf
Step 6: Solve for the final velocity
Now, we can solve for vf:
vf=−52=−2.5m/s
Conclusion
The speed of the combined mass after the collision is 2.5m/s in the negative direction (indicating it moves to the left).
Final Answer
The speed of the combined mass after the collision is 2.5m/s.
---
We have two identical balls moving towards each other. One ball is moving at a speed of 20 m/s to the right (let's consider this as positive direction), and the other ball is moving at a speed of 25 m/s to the left (which we will consider as negative direction).
Let the mass of each ball be m.
- Velocity of the first ball, v1=+20m/s
- Velocity of the second ball, v2=−25m/s
In a perfectly inelastic collision, the two objects stick together after the collision. According to the conservation of momentum:
Initial momentum=Final momentum
The initial momentum before the collision is given by:
pinitial=m⋅v1+m⋅v2=m⋅20+m⋅(−25)
pinitial=m(20−25)=m(−5)
After the collision, both balls move together with a common velocity vf. The final momentum is:
pfinal=(m+m)⋅vf=2m⋅vf
Setting the initial momentum equal to the final momentum gives:
m(−5)=2m⋅vf
We can cancel m from both sides (assuming m≠0):
−5=2vf
Now, we can solve for vf:
vf=−52=−2.5m/s
The speed of the combined mass after the collision is 2.5m/s in the negative direction (indicating it moves to the left).
The speed of the combined mass after the collision is 2.5m/s.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - A)
64 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - B)
35 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-J (AAKASH CHALLENGERS QUESTIONS)
14 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
Two identical balls each of mass 4 kg are moving towards each other with speeds 2 m/s and 3 m/s respectively. They undergo head on perfectly elastic collision. Then impulse imparted by one ball on other is
View SolutionTwo particles each of mass m are revolving in circular orbits of radius r=5R in opposite directions with orbital speed v0 . They collide perfectly inelastically and fall to the ground. The speed of combined mass on triking the ground will be
View Solution
Knowledge Check
Two identical balls A and B moving with velocities + 0.5 m/s and −0.3.m/s respectively collide head-on elastically. The velocities of the ball A and B after collision will be respectively
A+0.5m/sand+0.3m/sB−0.3m/sand+0.5m/sC + 0.3 m//s and + 0.5 m//sD−0.5m/sand+0.3m/s
Two identical balls each moving with speed v at right angle to each other collide perfectly inelastically. Their speed after collision is
View SolutionA particle of mass m moving in the x direction with speed 2v is hit by another particle of mass 2m moving in they y direction with speed v. If the collision is perfectly inelastic, the percentage loss in the energy during the collision is close to :
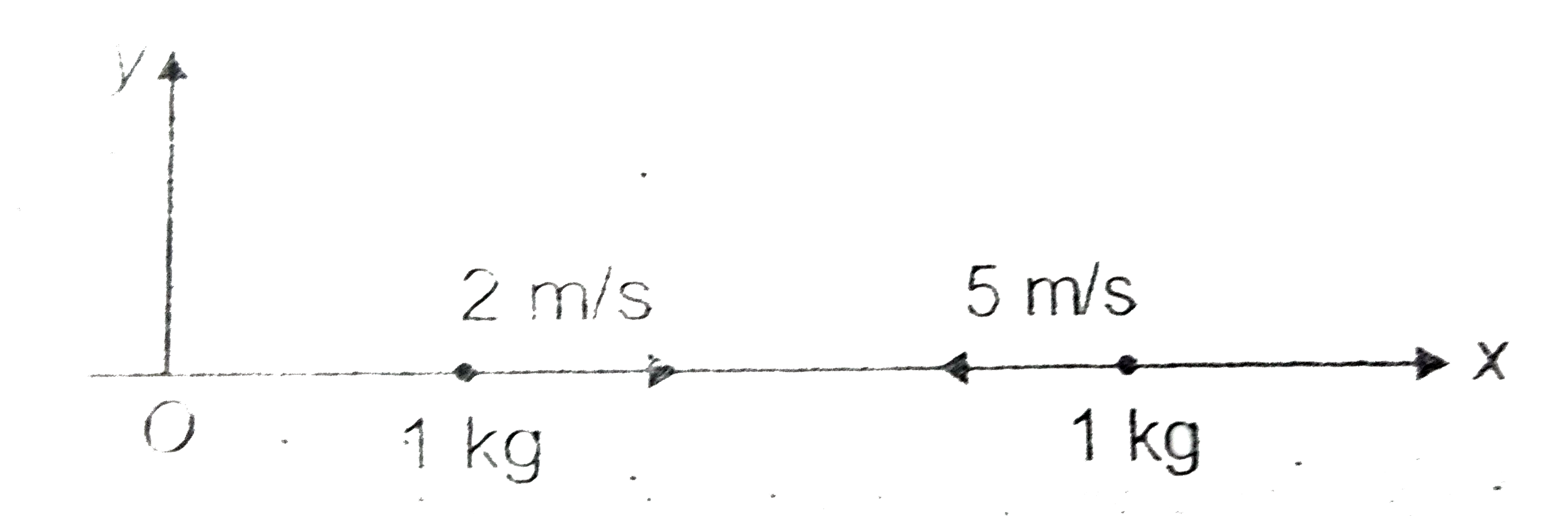
View SolutionTwo particles of mass 1 kg and 2 kg are moving with speed 2 m/s and 5 m/s as shown in the figure, they collides perfectly inelastically. And second particle come to rest after collision. Find
(a) Their final velocity
(b) Loss in kinetic energy
View SolutionTwo billiard balls A and B each of mass 50 g and moving in opposite directions with speed of 5m/s each, collide and rebound with the same speed if the collision lasts for 10−3 s which of the following statement(s) is (are) true?
View SolutionTwo particles of mass 2m and m moving with speed v and 2v respectively pependicular to each other collides perfectly inelastically, then

Speed of the particles after collision
View SolutionA body of mass M moving with a speed u has a ‘head on’, perfectly elastic collision with a body of mass m initially at rest. If M>>m , the speed of the body of mass m after collision, will be nearly :
View Solution(b) Two balls each of mass m moving in opposite direction with equal speed v collide head -on with each other . Predict the outcome of the collision assuming it perfectly elastic.
View Solution
