The potential energy of a particle of mass m is given by U=12kx2 for x<0 and U = 0 for x≥0. If total mechanical energy of the particle is E. Then its speed at x=√2Ek is
Zero
√2Em
√Em
√E2m
The correct Answer is:B
Step by step video & image solution for The potential energy of a particle of mass m is given by U=(1)/(2)kx^(2) for x lt 0 and U = 0 for x ge 0. If total mechanical energy of the particle is E. Then its speed at x = sqrt((2E)/(k)) is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-C (OBJECTIVE TYPE QUESTIONS) (MORE THAN ONE OPTIONS ARE CORRECT)
16 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-D (LINKED COMPREHENSION TYPE QUESTIONS) (COMPREHENSION-I)
3 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-A (OBJECTIVE TYPE QUESTIONS (ONE OPTIONISCORRECT)
60 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
The potential energy of a particle of mass 1 kg moving along x-axis given by U(x)=[x22−x]J. If total mechanical speed (in m/s):-
View SolutionThe potential energy of a particle of mass 2 kg in SHM is (9x2)J. Here x is the displacement from mean position . If total mechanical energy of the particle is 36 J. The maximum speed of the particle is
View SolutionThe potential energy of a particle of mass m free to move along the x-axis is given by U=(1/2)kx2 for x<0 and U=0 for x≥0 (x denotes the x-coordinate of the particle and k is a positive constant). If the total mechanical energy of the particle is E, then its speed at x=−√2E/k is
View SolutionThe potential energy of a particle of mass m free to move along the x-axis is given by U=(1/2)kx2 for x<0 and U=0 for x≥0 (x denotes the x-coordinate of the particle and k is a positive constant). If the total mechanical energy of the particle is E, then its speed at x=−√2E/k is
View SolutionThe potential energy of a particle oscillating along x-axis is given as
U=20+(x−2)2
Here, U is in joules and x in meters. Total mechanical energy of the particle is 36J.
(a) State whether the motion of the particle is simple harmonic or not.
(b) Find the mean position.
(c) Find the maximum kinetic energy of the particle.
View SolutionPotential energy of a particle in SHM along x - axis is gives by
U=10+(x−2)2
Here, U is in joule and x in metre. Total mechanical energy of the particle is 26J. Mass of the particle is 2kg. Find
(a) angular frequency of SHM,
(b) potential energy and kinetic energy at mean position and extreme position,
(c ) amplitude of oscillation,
(d) x - coordinates between which particle oscillates.
View SolutionThe potential energy of a particle moving along y axis is given by U(y)= 3y4+12y2 ,(where U is in joule and y is in metre). If total mechanical energy is 15 joule, then limits of motion are
View SolutionThe figure shows the variation of potential energy of a particle as a function pf x, the x-coordination of the region. It has been assumed that potential energy depends only on x. For all other values x,U is zero. i.e. forx<−10 and x>15,U=0.
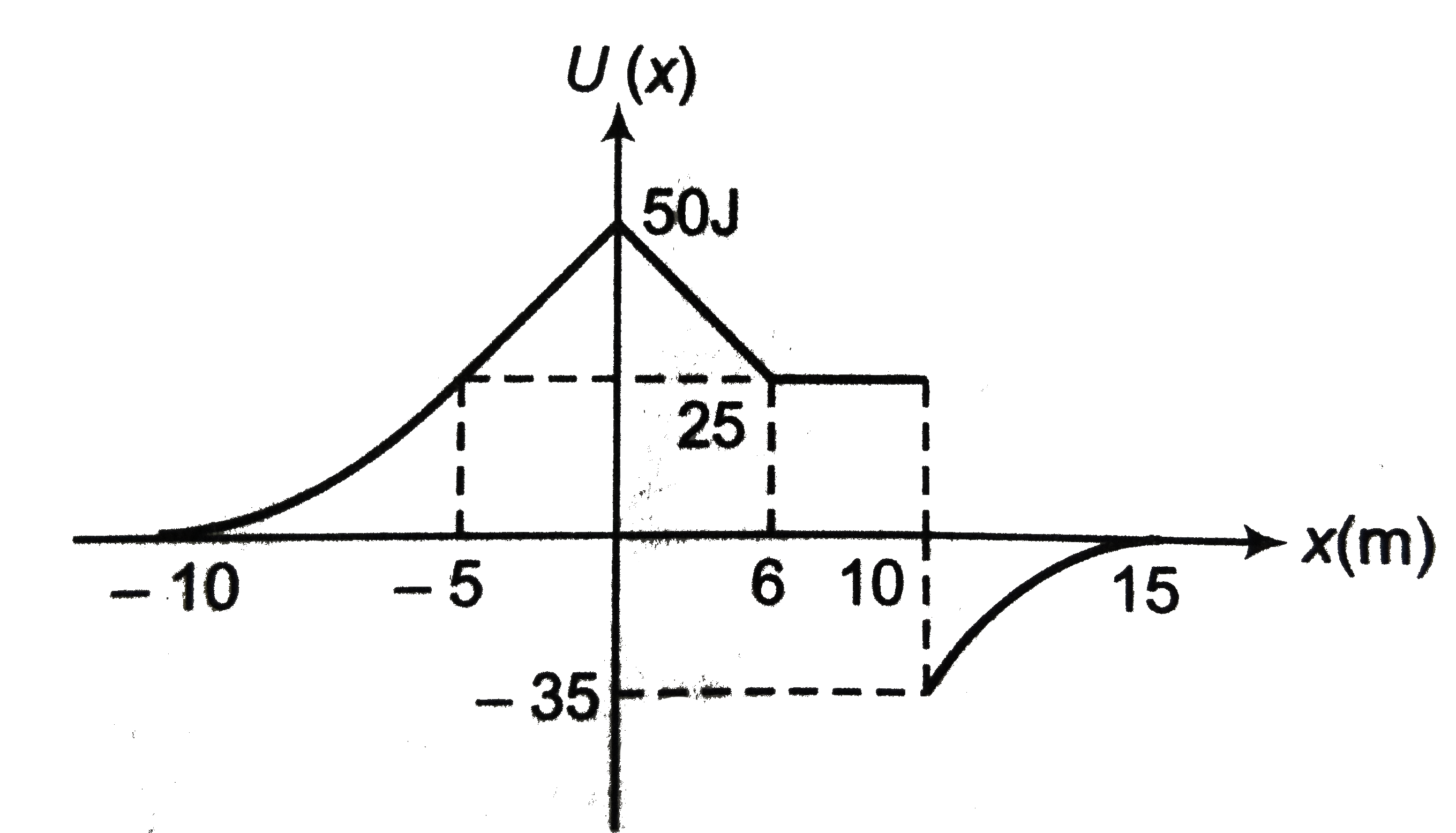
If total mechanical energy of the particle is 25J, then it can found in the region
View SolutionThe figure shows the variation of potential energy of a particle as a funcation of x, the x-coordinate of the region. It has been assumed that potential energy depends only on x. For all other values x,U is zero. i.e. forx<−10 and x>15,U=0.
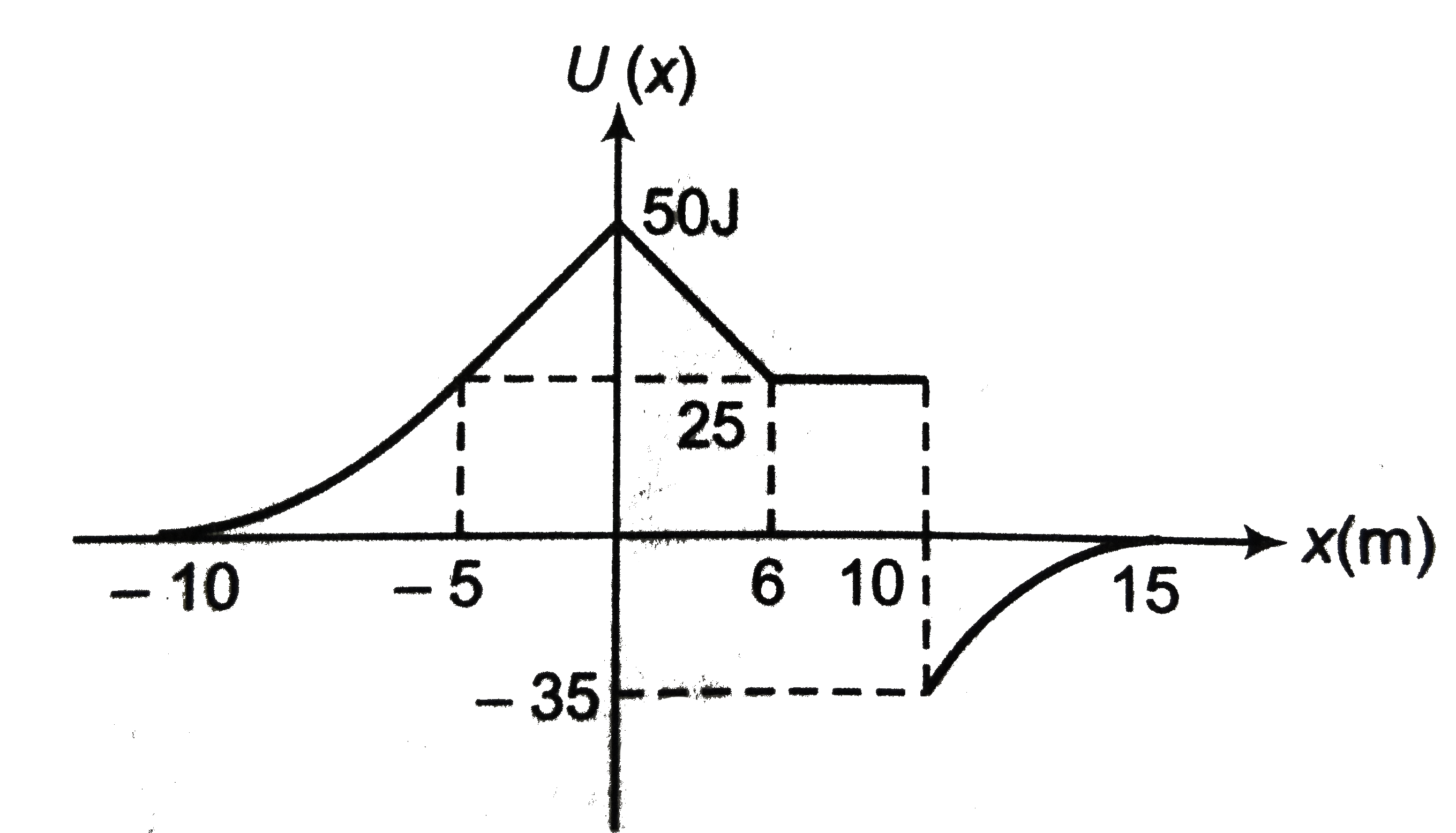
If total mechanical energy of the particle is −40J, then it can be found in region.
View Solutionathe potential energy of a particle of mass 2kg moving along the x-axis is given by U(x)=4x2−2x3( where U is in joules and x is in meters). The kinetic energy of the particle is maximum at
View Solution
