A particle of mass m is moving in a horizontal circle of radius r, under a centripetal force equal to −(k/r2) where k is constant. The total energy of the particle is
−Kr
1.5kr
−K2r
−3k2r
The correct Answer is:C
Step by step video & image solution for A particle of mass m is moving in a horizontal circle of radius r, under a centripetal force equal to -(k//r^2) where k is constant. The total energy of the particle is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-C (OBJECTIVE TYPE QUESTIONS) (MORE THAN ONE OPTIONS ARE CORRECT)
16 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-D (LINKED COMPREHENSION TYPE QUESTIONS) (COMPREHENSION-I)
3 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-A (OBJECTIVE TYPE QUESTIONS (ONE OPTIONISCORRECT)
60 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
A particle of mass m is moving in a horizontal circle of radius R under a centripetal force equal to −Ar2 (A = constant). The total energy of the particle is :-
(Potential energy at very large distance is zero)
View SolutionA particle of mass m is revolving in a horizontal circle of radius r under a centripetal force k/r2 where k is a constant. What is the total energy of the particle ?
View Solution
Knowledge Check
A particle of mass m is moving in a horizontal circle of radius r, under a centripetal force equal to (−K/r2), where k is a constant. The total energy of the particle is -
A−krB−k2rCk2rD2kr
If a particle of mass m is moving in a horizontal circle of radius r with a centripetal force (−1/r2) , the total energy is
View SolutionA particle of mass m moves along a horizontal circle of radius R such that normal acceleration of particle varies with time as an=kt2. where k is a constant.
Total force on particle at time t s is
View SolutionA particle of mass m moves along a horizontal circle of radius R such that normal acceleration of particle varies with time as an=kt2. where k is a constant.
Tangential force on particle at t s is
View SolutionA particle of mass m moves along a horizontal circle of radius R such that normal acceleration of particle varies with time as an=kt2. where k is a constant.
Power developed by total at time T is
View SolutionA particle of mass M is moving in a circle of fixed radius R in such a way that its centripetal acceleration at time t is given by n2Rt2 where n is a constant. The power delivered to the particle by the force acting on it, it :
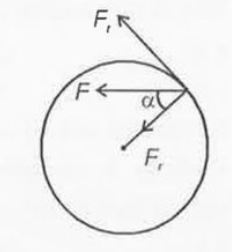
View SolutionA particle of mass m is moving in a circle of radius (r) with changing speed (v) the direction of centripetal force and tangential force are shown below the value of α is
View SolutionThe kinetic energy K of a particle moving along a circle of radius R depends upon the distance S as K=βS2 , where β is a constant. Tangential acceleration of the particle is proportional to
View Solution
