Question

A body is moved from rest along a straight line by a machine delivering constant power. The ratio of displacement and velocity $(s/v)$ varies with time $t$ as

Options

A.
B.
C.
D.

Answer

A

Explanation

To solve the problem, we need to analyze the relationship between displacement (s), velocity (v), and time (t) when a body is moved from rest by a machine delivering constant power (P).

1. Understanding Power:
Power (P) is defined as the rate of doing work. Mathematically, it can be expressed as:
\( P = \frac{W}{t} \)
where \(W\) is the work done and \(t\) is time.

2. Work Done:
Since the machine delivers constant power, the work done over time \(t\) can be expressed as:
\( W = Pt \)

3. Kinetic Energy Relation:
The work done on the body is converted into kinetic energy. Hence, we can write:
\( W = \frac{1}{2} mv^2 \)
Setting the two expressions for work equal gives:
\( Pt = \frac{1}{2} mv^2 \)

4. Solving for Velocity:
Rearranging the equation to solve for \(v^2\):
\( v^2 = \frac{2Pt}{m} \)
Taking the square root gives:
\( v = \sqrt{\frac{2P}{m}} \cdot t^{1/2} \)
Let \(k = \sqrt{\frac{2P}{m}}\), then:
\( v = kt^{1/2} \)

5. Finding Displacement:
The velocity \(v\) can also be expressed as the derivative of displacement \(s\) with respect to time \(t\):
\( v = \frac{ds}{dt} \)
Substituting our expression for \(v\):
\( \frac{ds}{dt} = kt^{1/2} \)
Rearranging gives:
\( ds = kt^{1/2} dt \)

6. Integrating to Find Displacement:
Integrating both sides to find \(s\):
\( s = \int kt^{1/2} dt \)
The integral of \(t^{1/2}\) is:
\( s = k \cdot \frac{2}{3} t^{3/2} + C \)
Since the body starts from rest, we can set the constant \(C = 0\):
\( s = \frac{2k}{3} t^{3/2} \)

7. Finding the Ratio \( \frac{s}{v} \):
Now, we need to find the ratio of displacement to velocity:
\( \frac{s}{v} = \frac{\frac{2k}{3} t^{3/2}}{kt^{1/2}} \)
Simplifying gives:
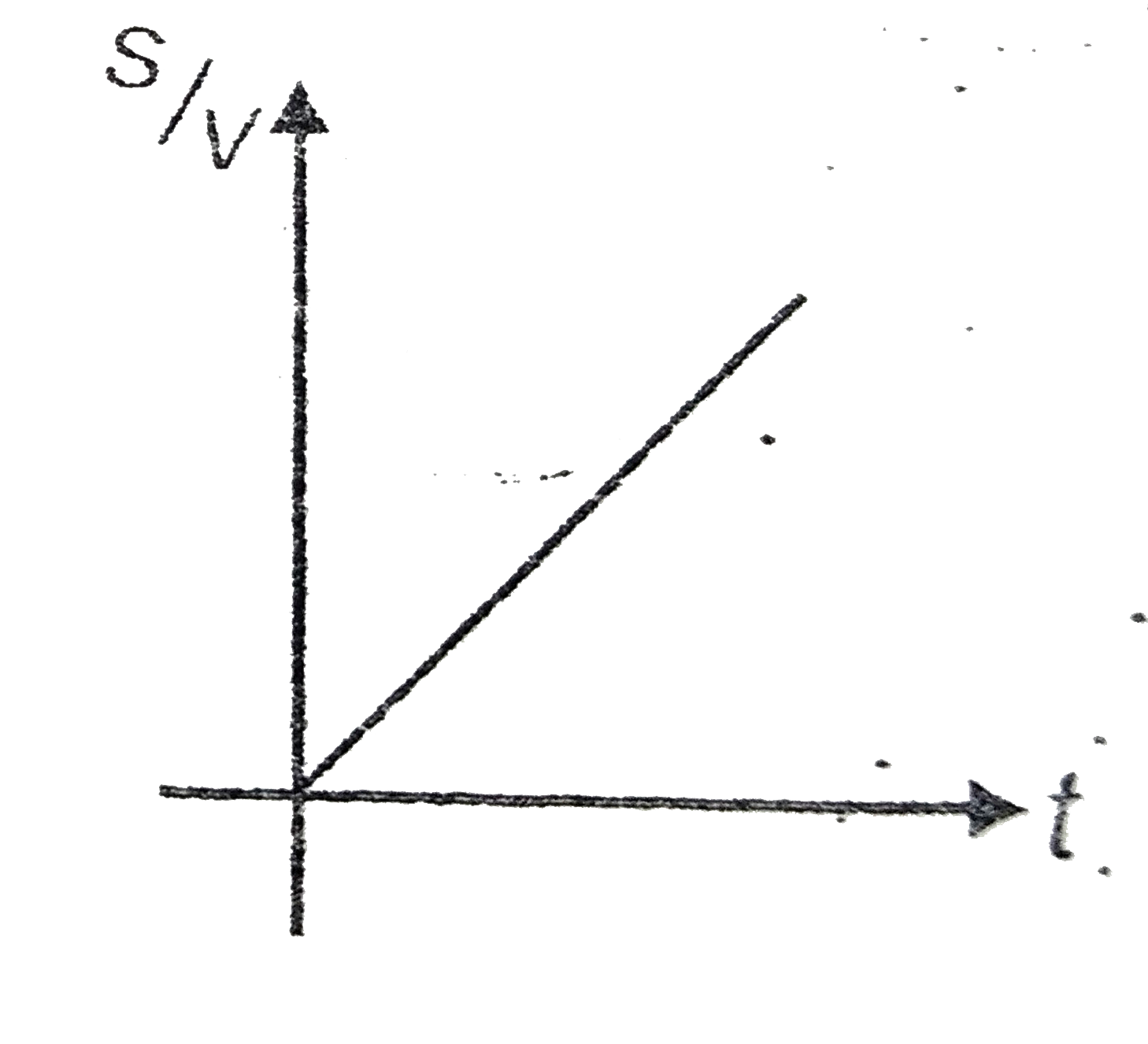
\( \frac{s}{v} = \frac{2}{3} t \)

8. Conclusion:
The ratio of displacement to velocity \( \frac{s}{v} \) varies linearly with time \(t\) as:
\( \frac{s}{v} = \frac{2}{3} t \)

Final Answer:
The ratio of displacement and velocity \( \frac{s}{v} \) varies with time \(t\) as \( \frac{s}{v} = \frac{2}{3} t \).