A particle of mass m is moving in a horizontal circle of radius R under a centripetal force equal to −Ar2 (A = constant). The total energy of the particle is :-
(Potential energy at very large distance is zero)
AR
−AR
A2R
−A2R
The correct Answer is:D
To find the total energy of a particle of mass m moving in a horizontal circle of radius R under a centripetal force given by −Ar2, we can follow these steps:
Step 1: Identify the centripetal force
The centripetal force Fc required to keep a particle moving in a circle is given by:
Fc=mv2R
According to the problem, the centripetal force is also given by:
Fc=−AR2
For our calculations, we will consider the magnitude of the force, so we can write:
mv2R=AR2
Step 2: Solve for mv2
From the equation above, we can rearrange it to solve for mv2:
mv2=AR
Step 3: Calculate the kinetic energy (KE)
The kinetic energy KE of the particle is given by:
KE=12mv2
Substituting mv2 from the previous step:
KE=12(AR)=A2R
Step 4: Find the potential energy (PE)
The potential energy U can be found using the relationship between force and potential energy:
F=−dUdr
Thus, we can express the potential energy as:
U=−∫Fdr
Substituting F=Ar2:
U=−∫R∞Ar2dr
Calculating the integral:
U=−(−Ar)R∞=−(0−AR)=−AR
Step 5: Calculate the total energy (TE)
The total energy E of the particle is the sum of its kinetic energy and potential energy:
E=KE+U
Substituting the values we found:
E=A2R−AR
Combining the terms:
E=A2R−2A2R=−A2R
Final Answer
Thus, the total energy of the particle is:
E=−A2R
The centripetal force Fc required to keep a particle moving in a circle is given by:
Fc=mv2R
According to the problem, the centripetal force is also given by:
Fc=−AR2
For our calculations, we will consider the magnitude of the force, so we can write:
mv2R=AR2
From the equation above, we can rearrange it to solve for mv2:
mv2=AR
The kinetic energy KE of the particle is given by:
KE=12mv2
Substituting mv2 from the previous step:
KE=12(AR)=A2R
The potential energy U can be found using the relationship between force and potential energy:
F=−dUdr
Thus, we can express the potential energy as:
U=−∫Fdr
Substituting F=Ar2:
U=−∫R∞Ar2dr
Calculating the integral:
U=−(−Ar)R∞=−(0−AR)=−AR
The total energy E of the particle is the sum of its kinetic energy and potential energy:
E=KE+U
Substituting the values we found:
E=A2R−AR
Combining the terms:
E=A2R−2A2R=−A2R
Thus, the total energy of the particle is:
E=−A2R
Topper's Solved these Questions
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 2
26 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 3
11 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - BOX-4
14 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
46 Videos
Similar Questions
A particle of mass m is revolving in a horizontal circle of radius r under a centripetal force k/r2 where k is a constant. What is the total energy of the particle ?
View SolutionIf a particle of mass m is moving in a horizontal circle of radius r with a centripetal force (−1/r2) , the total energy is
View Solution
Knowledge Check
A particle of mass m is moving in a horizontal circle of radius r, under a centripetal force equal to (−K/r2), where k is a constant. The total energy of the particle is -
A−krB−k2rCk2rD2kr
A particle of mass m describes a circle of radius r . The centripetal acceleration of the particle is 4r2 . What will be the momentum of the particle ?
View SolutionA particle of mass m moves along a horizontal circle of radius R such that normal acceleration of particle varies with time as an=kt2. where k is a constant.
Total force on particle at time t s is
View SolutionA charged particle of mass m is moving with a speed u in a circle of radius r. If the magnetic field induction at the centre is B, the charge on the particle is
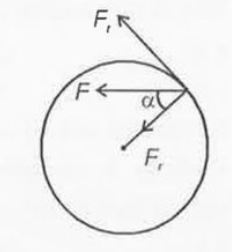
View SolutionA particle of mass m is moving in a circle of radius (r) with changing speed (v) the direction of centripetal force and tangential force are shown below the value of α is
View SolutionA particle of mass m moves along a horizontal circle of radius R such that normal acceleration of particle varies with time as an=kt2. where k is a constant.
Tangential force on particle at t s is
View SolutionA particle of mass M is moving in a circle of fixed radius R in such a way that its centripetal acceleration at time t is given by n2Rt2 where n is a constant. The power delivered to the particle by the force acting on it, it :
View SolutionA particle is moving in a circular path of radius a under the action of an attractive potential U=−k2r2. Its total energy is :
View Solution