If a particle of mass m is moving in a horizontal circle of radius r with a centripetal force (−1/r2) , the total energy is
−4r
−2r
−1r
−12r
The correct Answer is:D
mv2r=1r2i.e.,mv2=1r
∴K.E.=e22randP.E.=∫Fdtr=−e2r
∴ Total energy =K.E. + P.E.=e22r−e2r=−e22r
Similar Questions
A particle of mass m is moving in a horizontal circle of radius R under a centripetal force equal to −Ar2 (A = constant). The total energy of the particle is :-
(Potential energy at very large distance is zero)View SolutionA particle of mass m is revolving in a horizontal circle of radius r under a centripetal force k/r2 where k is a constant. What is the total energy of the particle ?
View Solution
Knowledge Check
- Question 1 - Select One
A particle of mass m is moving in a horizontal circle of radius r, under a centripetal force equal to (−K/r2), where k is a constant. The total energy of the particle is -
A−krB−k2rCk2rD2kr - Question 2 - Select One
A particle of mass M is moving in a horizontal circle fo radius R with unifomr speed V. When it moves from one point to a diameterically opposite point, its
Akinetic energy change by MV2/4Bmomentum does not changeCmomentum changes by 2 MVDkinetic energy changes by MV2
A particle of mass m is moving in a circle of radius (r) with changing speed (v) the direction of centripetal force and tangential force are shown below the value of α is
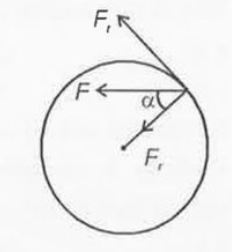 View Solution
View SolutionA particle is moving in a circular path of radius a under the action of an attractive potential U=−k2r2. Its total energy is :
View SolutionCentripetal acceleration of a particle of mass m moving in a circle of radius r is 4/r2. What is the angular momentum of the particle ?
View SolutionA particle of mass m moves along a horizontal circle of radius R such that normal acceleration of particle varies with time as an=kt2. where k is a constant.
Total force on particle at time t s isView SolutionA particle of mass M is moving in a circle of fixed radius R in such a way that its centripetal acceleration at time t is given by n2Rt2 where n is a constant. The power delivered to the particle by the force acting on it, it :
View SolutionA particle of mass m moves along a horizontal circle of radius R such that normal acceleration of particle varies with time as an=kt2. where k is a constant.
Tangential force on particle at t s isView Solution
