A particle is acted upon by a force →F=yˆi+xˆj newton. When the particle is moved from (1 m, 1 m) to (9m, 3 m) via straight path, work done by →F is y. What is the value of xy?
The correct Answer is:1
To solve the problem step by step, we will calculate the work done by the force vector →F=y^i+x^j as the particle moves from point A (1 m, 1 m) to point B (9 m, 3 m).
Step 1: Identify the force and the displacement
The force acting on the particle is given by:
→F=y^i+x^j
The initial position (point A) is (x1,y1)=(1,1) and the final position (point B) is (x2,y2)=(9,3).
Step 2: Express the differential displacement vector
The differential displacement vector d→r can be expressed as:
d→r=dx^i+dy^j
Step 3: Calculate the work done
The work done W by the force →F when moving from point A to point B is given by the integral:
W=∫BA→F⋅d→r
Substituting the expressions for →F and d→r:
W=∫x2x1(y^i+x^j)⋅(dx^i+dy^j)
This expands to:
W=∫x2x1ydx+∫y2y1xdy
Step 4: Set the limits of integration
Here, the limits for x are from 1 to 9, and for y from 1 to 3:
W=∫91ydx+∫31xdy
Step 5: Evaluate the integrals
1. For the first integral, since y is constant (equal to 1 when x=1):
W1=y∫91dx=y(x)91=y(9−1)=8y
2. For the second integral, since x is constant (equal to 1 when y=1):
W2=x∫31dy=x(y)31=x(3−1)=2x
Step 6: Combine the results
Thus, the total work done W is:
W=8y+2x
According to the problem, this work done is equal to y:
8y+2x=y
Step 7: Rearrange the equation
Rearranging gives:
2x=y−8y
2x=−7y
xy=−72
Final Answer
The value of xy is:
xy=−72
The force acting on the particle is given by:
→F=y^i+x^j
The initial position (point A) is (x1,y1)=(1,1) and the final position (point B) is (x2,y2)=(9,3).
The differential displacement vector d→r can be expressed as:
d→r=dx^i+dy^j
The work done W by the force →F when moving from point A to point B is given by the integral:
W=∫BA→F⋅d→r
Substituting the expressions for →F and d→r:
W=∫x2x1(y^i+x^j)⋅(dx^i+dy^j)
This expands to:
W=∫x2x1ydx+∫y2y1xdy
Here, the limits for x are from 1 to 9, and for y from 1 to 3:
W=∫91ydx+∫31xdy
1. For the first integral, since y is constant (equal to 1 when x=1):
W1=y∫91dx=y(x)91=y(9−1)=8y
2. For the second integral, since x is constant (equal to 1 when y=1):
W2=x∫31dy=x(y)31=x(3−1)=2x
Thus, the total work done W is:
W=8y+2x
According to the problem, this work done is equal to y:
8y+2x=y
Rearranging gives:
2x=y−8y
2x=−7y
xy=−72
The value of xy is:
xy=−72
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-H (MULTIPLE TRUE FALSE TYPE QUESTIONS)
10 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-I (SUBJECTIVE TYPE QUESTIONS)
6 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-F (MATRIX-MATCH TYPE QUESTIONS)
5 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
A constant force F=(ˆi+3ˆj+4ˆk)N acts on a particle and displace it from (-1m,2m,1m)to(2m,-3m,1m).
View SolutionIf force →f=(3x→i+y2→j) N is acting on a body and body moves from (1m, 2m, 1m) to (2m, 3, 8m), then find the work done due to the force
View SolutionThe work done by a force →F=(−6x2ˆi)N in displacing a particle from x = 4mtox = -2mis
View SolutionA body of mass 2 kg is acted upon by two forces →D1=(2ˆi+3ˆj)Nand→F2(−2ˆk+3ˆj)N. If the body is displaced from A(3m,−2m,1m) to B (−1m,+2m,−3m), then work done on the body is
View SolutionA force bar F = (3hat i-4 hat j +b hat k)N is acting on the particle which is moving from point A ( 0-1, 1) m to the point B(2, 2 3) m If net work done by the force on the particle is zero then value of b is
View SolutionThe work done by a force →F=(−6x3ˆi) N in displacing a particle from x = 4m to x = - 2m is
View SolutionA force →F=(3ˆi+4ˆj) N is acting on a particle. Work done by the force is zero, when particle is moving on the line 2y+Px=2, the value of P is
View SolutionA force given by →F=fxˆi+fyˆj+fzˆk acts on a particle which moves from (a, b, c) to (d, e, f). The work done by the force F is : (Here A1,A2,A3 are magntitude of area bounded )
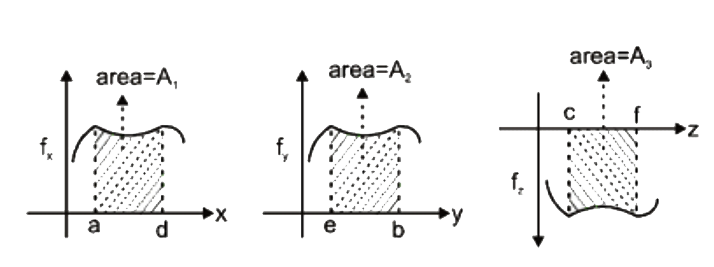
View SolutionA particle of mass 'm' moves along the quarter section of the circular path whose centre is at the origin . The radius of the circular path is 'a'. A force →F=yˆi−xˆj newton acts on the particle, where x,y denote the coordinates of position of the particle. Calculate the work done by this force in taking, the particle from point, A(a,0) to point B(0,a) along the circular path.
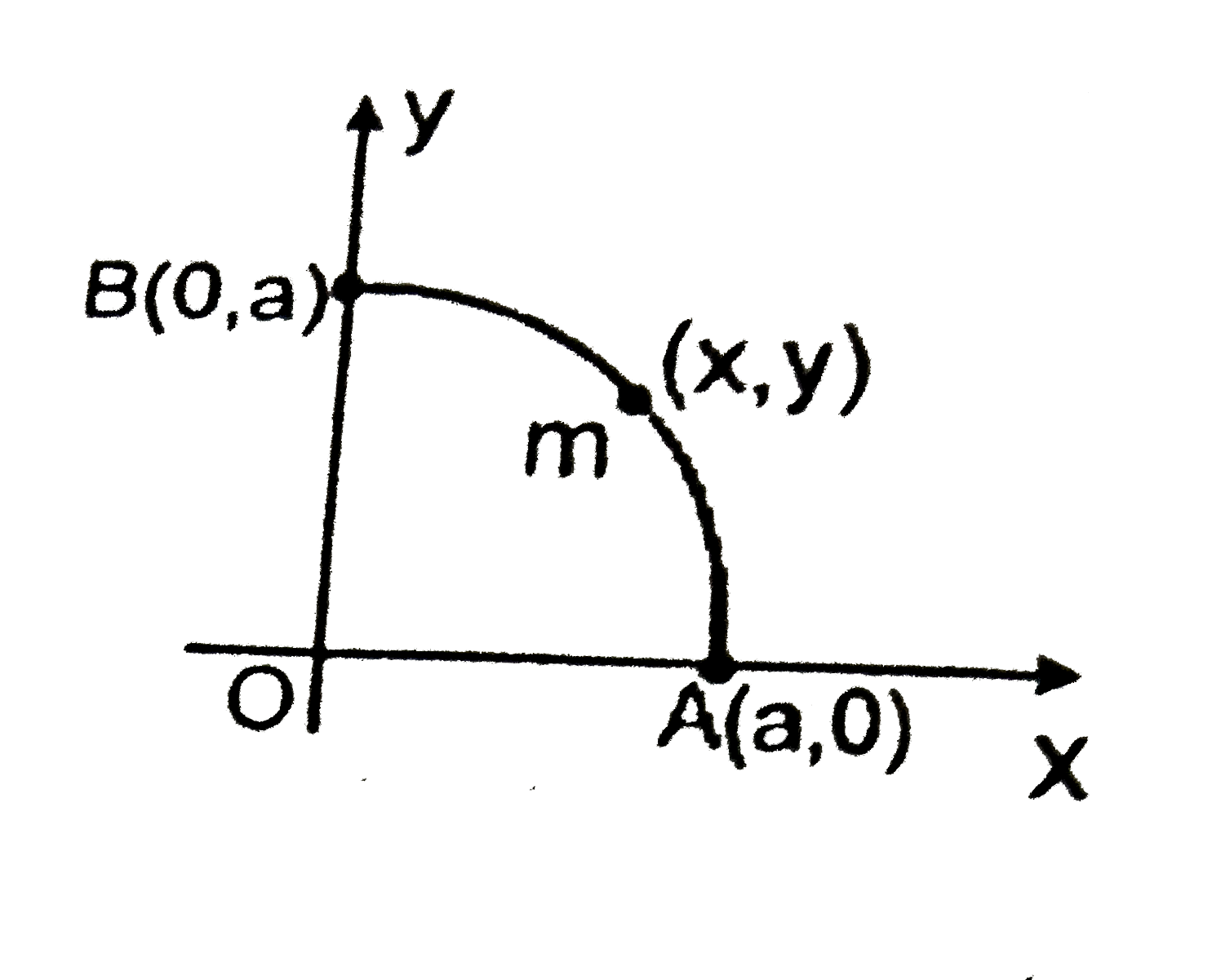
View SolutionThe work done by the forces →F=2ˆi−3ˆj+2ˆk in moving a particle from (3,4,5) to (1,2,3) is (A) 0 (B) 32 (C) −4 (D) −2
View Solution
