Two identical billiard balls are in contact on a table. A third identical ball strikes them symmetrically and comes to rest after impact. The coefficient of restitution is :
23
32
13
12
To solve the problem, we will follow these steps:
Step 1: Understand the scenario
We have three identical billiard balls. The third ball strikes the first two balls symmetrically, causing the third ball to come to rest after the impact. The first two balls will move apart after the collision.
Step 2: Define the variables
- Let the mass of each billiard ball be m.
- Let the initial velocity of the third ball (the one that strikes) be v0.
- Let the final velocity of the first and second balls after the collision be v.
Step 3: Analyze the collision
Since the third ball comes to rest after the impact, we can apply the conservation of momentum. The initial momentum of the system is given by the momentum of the third ball, which is mv0.
Step 4: Apply conservation of momentum
The total final momentum of the two balls after the collision can be expressed as:
Final momentum=m⋅v+m⋅v=2mv
Setting the initial momentum equal to the final momentum gives:
mv0=2mv
Dividing by m (since m is not zero):
v0=2v⇒v=v02
Step 5: Determine the angle of separation
Since the balls are struck symmetrically, they will move apart at equal angles. The angle between their paths will be 60∘ (as they form an equilateral triangle). Therefore, each ball will move at an angle of 30∘ from the line of impact.
Step 6: Resolve the velocities
The horizontal and vertical components of the velocities for each ball can be resolved:
- For Ball 1:
- Horizontal component: vcos(30∘)
- Vertical component: vsin(30∘)
- For Ball 2:
- Horizontal component: vcos(30∘)
- Vertical component: −vsin(30∘) (opposite direction)
Step 7: Calculate the coefficient of restitution
The coefficient of restitution e is defined as the ratio of the relative velocity of separation to the relative velocity of approach.
1. Velocity of separation: After the collision, the balls separate with a velocity v.
2. Velocity of approach: The approach velocity of the third ball before impact is v0.
Using the formula for the coefficient of restitution:
e=Velocity of separationVelocity of approach=vv0
Step 8: Substitute the values
From our earlier calculations:
- We found v=v02.
- The velocity of approach is v0.
Substituting these into the equation for e:
e=v02v0=12
Step 9: Final calculation
However, we need to consider the angle of separation. The effective velocity of separation in the direction of the impact is:
veffective=vcos(30∘)
Thus:
e=vcos(30∘)v0=v02⋅√32v0=√34
Step 10: Conclusion
The coefficient of restitution is:
e=2√3
We have three identical billiard balls. The third ball strikes the first two balls symmetrically, causing the third ball to come to rest after the impact. The first two balls will move apart after the collision.
- Let the mass of each billiard ball be m.
- Let the initial velocity of the third ball (the one that strikes) be v0.
- Let the final velocity of the first and second balls after the collision be v.
Since the third ball comes to rest after the impact, we can apply the conservation of momentum. The initial momentum of the system is given by the momentum of the third ball, which is mv0.
The total final momentum of the two balls after the collision can be expressed as:
Final momentum=m⋅v+m⋅v=2mv
Setting the initial momentum equal to the final momentum gives:
mv0=2mv
Dividing by m (since m is not zero):
v0=2v⇒v=v02
Since the balls are struck symmetrically, they will move apart at equal angles. The angle between their paths will be 60∘ (as they form an equilateral triangle). Therefore, each ball will move at an angle of 30∘ from the line of impact.
The horizontal and vertical components of the velocities for each ball can be resolved:
- For Ball 1:
- Horizontal component: vcos(30∘)
- Vertical component: vsin(30∘)
- Horizontal component: vcos(30∘)
- Vertical component: −vsin(30∘) (opposite direction)
The coefficient of restitution e is defined as the ratio of the relative velocity of separation to the relative velocity of approach.
2. Velocity of approach: The approach velocity of the third ball before impact is v0.
e=Velocity of separationVelocity of approach=vv0
From our earlier calculations:
- We found v=v02.
- The velocity of approach is v0.
e=v02v0=12
However, we need to consider the angle of separation. The effective velocity of separation in the direction of the impact is:
veffective=vcos(30∘)
Thus:
e=vcos(30∘)v0=v02⋅√32v0=√34
The coefficient of restitution is:
e=2√3
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - C) Objective Type Questions (More than one option are correct)
29 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - D) Linked Comprehension Type Questions
20 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - A) Objective Type Questions (One option is correct)
62 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE
21 Videos
Similar Questions
Two billiard balls of same size and mass are in contact on a billiard table. A third ball of same mass and size strikes them symmetrically and remains at rest after the impact. Find the coefficient of restitution between the balls?
View SolutionTwo billiard balls of same size and mass are in contact on a billiard table. A third ball of same mass and size strikes them symmetrically and remains at rest after the impact. Find the coefficient of restitution between the balls?
View Solution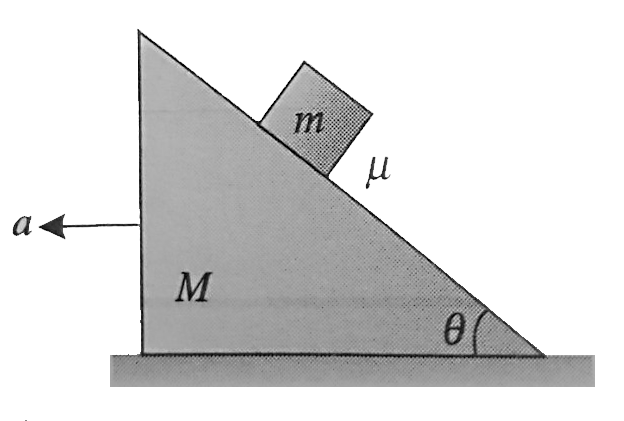
A block of mass m is at rest relative to the stationary wedge of mass M. The coefficient of friction between block and wedge is μ. The wedge is now pulled horizontally with acceleration a as shown in figure. Then the minimum magnitude of a for the friction between block and wedge to be zero is:
View SolutionA ball of mass m moving at a speed v collides with another ball of mass 3m at rest. The lighter block comes to rest after collisoin. The coefficient of restitution is
View SolutionA ball collides with an inclined plane of inclination θ after falling through a distance h. if it moves horizontal just after the impact, the coefficient of restitution is
View SolutionTwo equal spheres of mass m are in contact on a smooth horizontal table. A third identical sphere impinges symmetrically on the and is reduced to rest. Prove that e=23 and find the loss in KE.
View SolutionBall 1 collides directly with another identical ball 2 at rest. Velocity of second ball becomes two times that of 1 after collison. Find the coefficient of restitution between the two balls?
View SolutionBall 1 collides directly with another identical ball 2 at rest. Velocity of second ball becomes two times that of 1 after collison. Find the coefficient of restitution between the two balls?
View SolutionA tennis ball bounces down a flight of stairs, striking each step in turn and rebounding to half to height of the step. The coefficient of restitution is
View SolutionA ball of mass m moving at a speed v makes a head on inelastic collision with an identical ball at rest. The kinetic energy of the balls after the collision is 34th of the original. Find the coefficient of restitution.


View Solution
