A uniform solid cylinder having height l and diameter d is placed on a rough horizontally plank which is being pulled horizontal with an acceleration. Find the maximum value of the acceleration for which the cylinder remain in equilibrium
gdl
gd2l
gld
gl2d
To solve the problem of finding the maximum value of acceleration for which the cylinder remains in equilibrium on a rough horizontal plank, we can follow these steps:
Step 1: Understand the Forces Acting on the Cylinder
The cylinder has the following forces acting on it:
- Weight (mg) acting downwards.
- Normal force (N) acting upwards.
- Frictional force (F) acting horizontally opposite to the direction of the plank's acceleration.
Step 2: Set Up the Free Body Diagram
Draw a free body diagram for the cylinder. The forces acting on it are:
- The weight (mg) acting downwards at the center of the cylinder.
- The normal force (N) acting upwards at the point of contact with the plank.
- The frictional force (F) acting horizontally.
Step 3: Apply Newton's Second Law
Since the plank is accelerating with an acceleration A, the cylinder experiences a pseudo force Fpseudo=ma acting in the opposite direction of the acceleration of the plank. For the cylinder to remain in equilibrium, the frictional force must equal the pseudo force:
F=ma
Where m is the mass of the cylinder and a is the acceleration of the plank.
Step 4: Analyze Torque About the Center of Mass
The frictional force will create a torque about the center of mass of the cylinder. The torque due to the frictional force (F) about the center of mass is given by:
τ=F⋅d2
And the torque due to the weight of the cylinder (mg) is:
τweight=mg⋅d2
For the cylinder to remain in equilibrium, the net torque about the center of mass must be zero:
F⋅d2−mg⋅d2=0
Step 5: Solve for the Frictional Force
From the torque balance equation:
F⋅d2=mg⋅d2
Cancelling d2 from both sides gives:
F=mg
Step 6: Substitute the Frictional Force into the Equation
From Step 3, we have:
F=ma
Substituting F=mg into this equation gives:
mg=ma
This implies:
a=g
Step 7: Relate the Acceleration to the Dimensions of the Cylinder
Now, we need to consider the dimensions given in the problem. The maximum acceleration A for which the cylinder remains in equilibrium can be expressed as:
A=gDL
where D is the diameter and L is the height of the cylinder.
Conclusion
Thus, the maximum value of the acceleration A for which the cylinder remains in equilibrium is:
Amax=gDL
The cylinder has the following forces acting on it:
- Weight (mg) acting downwards.
- Normal force (N) acting upwards.
- Frictional force (F) acting horizontally opposite to the direction of the plank's acceleration.
Draw a free body diagram for the cylinder. The forces acting on it are:
- The weight (mg) acting downwards at the center of the cylinder.
- The normal force (N) acting upwards at the point of contact with the plank.
- The frictional force (F) acting horizontally.
Since the plank is accelerating with an acceleration A, the cylinder experiences a pseudo force Fpseudo=ma acting in the opposite direction of the acceleration of the plank. For the cylinder to remain in equilibrium, the frictional force must equal the pseudo force:
F=ma
Where m is the mass of the cylinder and a is the acceleration of the plank.
The frictional force will create a torque about the center of mass of the cylinder. The torque due to the frictional force (F) about the center of mass is given by:
τ=F⋅d2
And the torque due to the weight of the cylinder (mg) is:
τweight=mg⋅d2
For the cylinder to remain in equilibrium, the net torque about the center of mass must be zero:
F⋅d2−mg⋅d2=0
From the torque balance equation:
F⋅d2=mg⋅d2
Cancelling d2 from both sides gives:
F=mg
From Step 3, we have:
F=ma
Substituting F=mg into this equation gives:
mg=ma
This implies:
a=g
Now, we need to consider the dimensions given in the problem. The maximum acceleration A for which the cylinder remains in equilibrium can be expressed as:
A=gDL
where D is the diameter and L is the height of the cylinder.
Thus, the maximum value of the acceleration A for which the cylinder remains in equilibrium is:
Amax=gDL
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - C) Objective Type Questions (More than one option are correct)
29 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - D) Linked Comprehension Type Questions
20 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - A) Objective Type Questions (One option is correct)
62 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE
21 Videos
Similar Questions

A uniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force F is applied at the top point P of the cylinder so that it start pure rolling. The acceleration of the cylinder is
View SolutionA container shown in Fig. is accelerated horizontally with acceleration a.
a. Find the minimum value of a at which liquid just starts spilling out.

View SolutionA uniform solid cyinder of radius R=15cm rolls over a horizontal plane passing into an inclined plane forming an ange α=30∘ with the horizontal. Find the maximum value of the velocity v0 which still permits the cylinder to roll on the inclined plane section without a jump. (The sliding is asumed to be absent).

View SolutionUniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force is applied at the top point P of the cylinder so that it start pure rolling .In the above question, the frictional force on the cylinder is
View SolutionA uniform cylinder of mass M and radius R is placed on a rough horizontal board, which in turn is placed on a smooth surface. The coefficient of friction between the board and the cylinder is μ. If the board starts accelerating with constant acceleration a, as shown in the figure, then

Option1
for pure rolling motion of the cylinder, direction of frictional force is forward and its magnitude is M a / 3
Option2
the maximum value of a, so that cyliner performs pure rolling is 3 μ g
Option3
The acceleration of the centre of mass of te cylinder under pure rolling condition for the given a is a / 3
Option4
none of these
View SolutionA solid sphere of radius R is placed on a smooth horizontal surface. A horizontal force F is applied at height h from the lowest point. For the maximum acceleration of the centre of mass
View SolutionA solid sphere of radius R is placed on a smooth horizontal surface. A horizontal force F is applied at height h from the lowest point. For the maximum acceleration of the centre of mass
View SolutionA uniform solid cylinder of mass m rests on two horizontal planks. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically down with a constant force F.
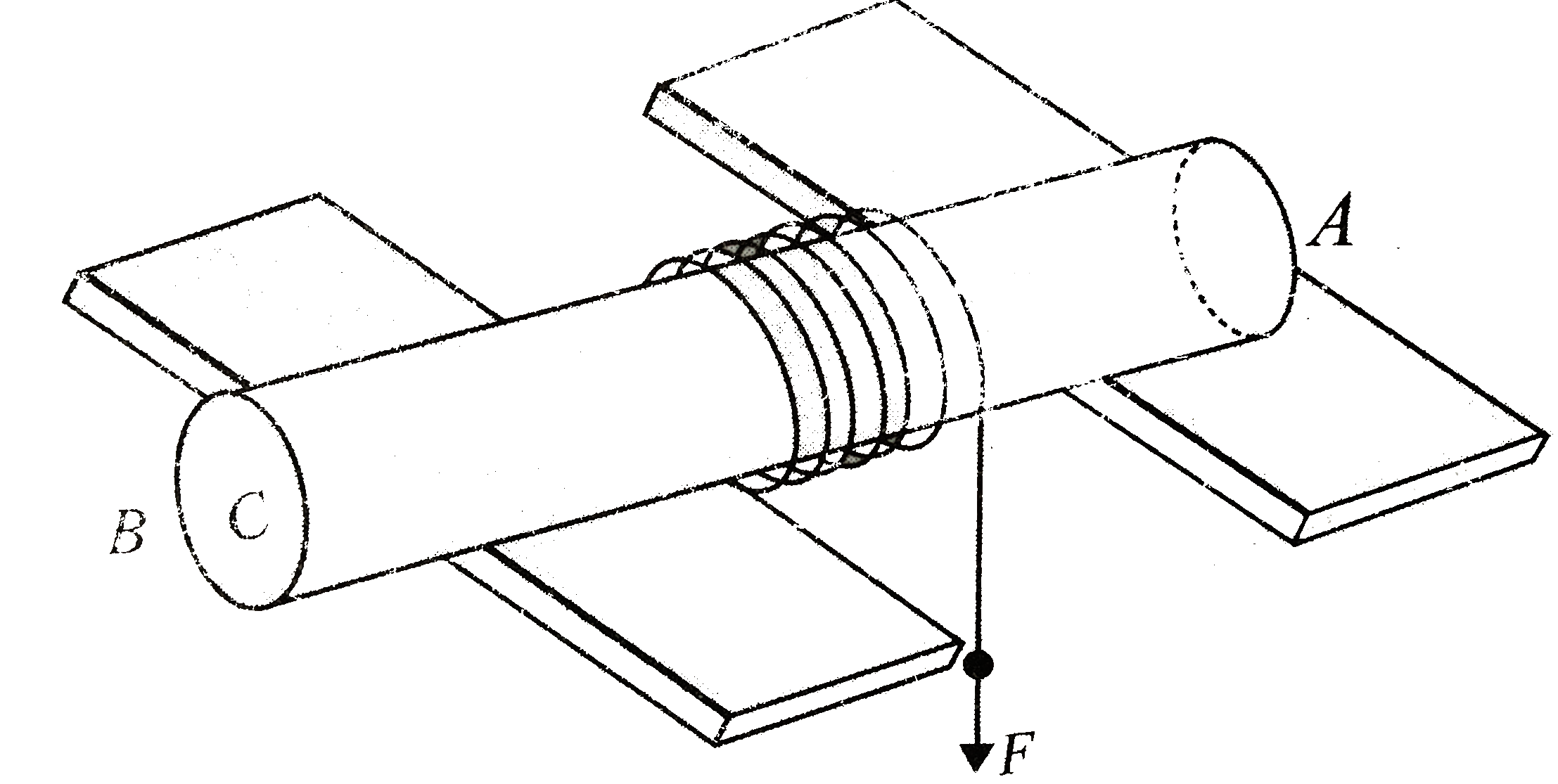
Find the maximum magnitude of the force F which may be applied without bringing about any sliding of the cylinder, if the coefficient of friction between the plank and the cylinder is equal to μ. What is the maximum acceleration of the centre of mass over the planks?
View SolutionA uniform solid cylindrical roller of mass 'm' is being pulled on a horizontal surface with force F parallel to the surface and applied at its centre. If the acceleration of the cylinder is 'a' and it is rolling without slipping, then the value of 'F' is :−
View SolutionConsider a cylinder of mass M resting on a rough horizontal rug that is pulled out from under it with acceleration 'a' perpendicular to the axis of the cylinder. What is Ffriction at point P ? It is assumed that the cylinder does not slip.

View Solution
