Will the velocity and acceleration of centre of mass change if particles A, B and C are projected from different locations but with same velocities ?
To solve the question, we need to analyze the situation of three particles A, B, and C being projected from different locations but with the same velocity. We will determine if the velocity and acceleration of the center of mass (CM) of the system change under these conditions.
1. Define the System:
Let the masses of particles A, B, and C be mA, mB, and mC respectively. Assume they are projected with the same velocity v0.
2. Velocity of Center of Mass:
The formula for the velocity of the center of mass (CM) is given by:
VCM=mAvA+mBvB+mCvCmA+mB+mC
Since all particles are projected with the same velocity v0, we have:
vA=vB=vC=v0
Substituting these values into the equation gives:
VCM=mAv0+mBv0+mCv0mA+mB+mC
Factoring out v0:
VCM=(mA+mB+mC)v0mA+mB+mC=v0
Thus, the velocity of the center of mass is v0.
3. Acceleration of Center of Mass:
The acceleration of the center of mass is given by:
aCM=mAaA+mBaB+mCaCmA+mB+mC
Here, aA, aB, and aC are the accelerations of particles A, B, and C respectively. Since all particles are projected with the same velocity and we assume they are under the same acceleration (for example, due to gravity), we can write:
aA=aB=aC=a
Substituting these values gives:
aCM=mAa+mBa+mCamA+mB+mC=(mA+mB+mC)amA+mB+mC=a
Thus, the acceleration of the center of mass is equal to the common acceleration a.
4. Conclusion:
Since both the velocity and acceleration of the center of mass depend only on the common velocity and acceleration of the particles, and not on their individual locations, we conclude that:
- The velocity of the center of mass does not change if particles A, B, and C are projected from different locations but with the same velocity.
- The acceleration of the center of mass also does not change under the same conditions.
Final Answer:
No, the velocity and acceleration of the center of mass do not change if particles A, B, and C are projected from different locations but with the same velocities.
---
Let the masses of particles A, B, and C be mA, mB, and mC respectively. Assume they are projected with the same velocity v0.
The formula for the velocity of the center of mass (CM) is given by:
VCM=mAvA+mBvB+mCvCmA+mB+mC
Since all particles are projected with the same velocity v0, we have:
vA=vB=vC=v0
Substituting these values into the equation gives:
VCM=mAv0+mBv0+mCv0mA+mB+mC
Factoring out v0:
VCM=(mA+mB+mC)v0mA+mB+mC=v0
Thus, the velocity of the center of mass is v0.
The acceleration of the center of mass is given by:
aCM=mAaA+mBaB+mCaCmA+mB+mC
Here, aA, aB, and aC are the accelerations of particles A, B, and C respectively. Since all particles are projected with the same velocity and we assume they are under the same acceleration (for example, due to gravity), we can write:
aA=aB=aC=a
Substituting these values gives:
aCM=mAa+mBa+mCamA+mB+mC=(mA+mB+mC)amA+mB+mC=a
Thus, the acceleration of the center of mass is equal to the common acceleration a.
Since both the velocity and acceleration of the center of mass depend only on the common velocity and acceleration of the particles, and not on their individual locations, we conclude that:
- The velocity of the center of mass does not change if particles A, B, and C are projected from different locations but with the same velocity.
- The acceleration of the center of mass also does not change under the same conditions.
No, the velocity and acceleration of the center of mass do not change if particles A, B, and C are projected from different locations but with the same velocities.
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - J) Aakash Challengers Questions
13 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE
21 Videos
Similar Questions
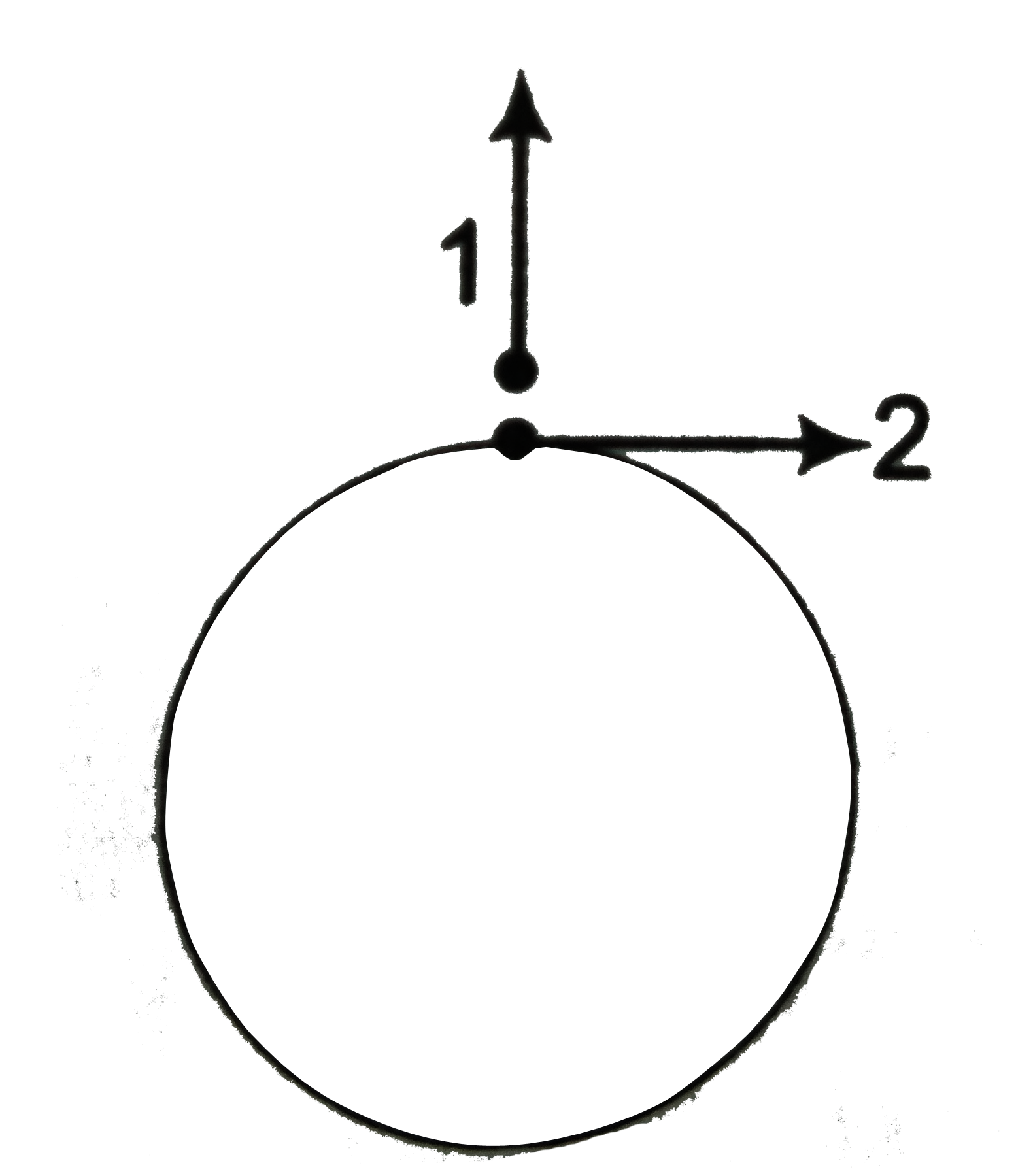
Two identical particles 1 and 2 are projected from surface of earth with same velocities in the directions shows in figure.
View SolutionA nonzero external force acts on a system of particles. The velocity and the acceleration of the centre of mass are found to bev0anda0 at an instant t. It is possible that:
View SolutionA satellite is orbiting around the earth in a circular orbit of radius r. A particle of mass m is projected from the satellite in a forward direction with a velocity v=2/3 times the orbital velocity (this velocity is given w.r.t. earth). During subsequent motion of the particle, its minimum distance from the centre of earth is
View SolutionAssertion: In projectile motion horizontal velocity remains same but vertical velocity continously change Reason: particle strikes the ground with same vertical velocity with which the particle was thrwon in vertical direction.
View SolutionLet v and a be the instantaneous velocity and acceleration of a particle moving in a plane. Then rate of change of speed dvdt of the particle is equal to
View SolutionStatement-I : When velocity of a particle is zero then acceleration of particle is zero.
Statement-II : Acceleration is equal to rate of change of velocity.
View SolutionGive examples where a. the velocity of a particle is zero but its acceleration is not zero. b.the velocity is opposite in direction to the acceleration, c. the velocity is perpendicular to the acceleration.
View SolutionA particle A is projected from the ground with an initial velocity of 10m/s at an angle of 60∘ with horizontal. From what height should an another particle B be projected horizontally with velocity 5m/s so that both the particles collide in ground at point C if both are projected simultaneously g=10m/s2.

View SolutionTwo balls A and B are projected vertically upwards with different velocities. What is the relative acceleration between them?
View Solution
For a particle moving along straight line with constant acceleration (a), we define velocity of the particle with time as
v=u+at, (u=initial velocity)
Draw the velocity-time graph of the particle in following situations.
(i) Velocity is decresing with time (i.e., acceleration in negative)
(ii) Initial velocity is negative but acceleration is positive
View Solution