Let v and a be the instantaneous velocity and acceleration of a particle moving in a plane. Then rate of change of speed dvdt of the particle is equal to
|a|
v.av
the component of a parallel to v
the component of a perpendicular to v
The correct Answer is:B, C
To find the rate of change of speed dvdt of a particle moving in a plane, we can follow these steps:
Step 1: Understand the Definitions
- Instantaneous Velocity (v): The velocity of the particle at a specific instant.
- Instantaneous Acceleration (a): The acceleration of the particle at a specific instant.
Step 2: Identify the Rate of Change of Speed
The rate of change of speed is defined as:
dvdt
This represents how quickly the speed of the particle is changing over time.
Step 3: Relate Speed Change to Acceleration
The rate of change of speed is associated with the tangential component of acceleration (at), which is the component of acceleration that acts in the direction of the velocity. Therefore, we can express this as:
dvdt=at
Step 4: Resolve Acceleration into Components
The total acceleration a can be resolved into two components:
1. Tangential Acceleration (at): This is the component of acceleration in the direction of the velocity.
2. Normal Acceleration (an): This is the component of acceleration perpendicular to the velocity.
Step 5: Calculate Tangential Acceleration
The tangential acceleration can be calculated using the angle θ between the velocity vector v and the acceleration vector a:
at=acos(θ)
Alternatively, using the dot product:
at=a⋅v|v|
where a⋅v is the dot product of the acceleration and velocity vectors.
Step 6: Conclusion
Thus, we can conclude that the rate of change of speed dvdt is equal to the tangential component of acceleration, which can be expressed as:
dvdt=at=a⋅v|v|
Final Answer
The rate of change of speed dvdt of the particle is equal to the component of acceleration parallel to the velocity, or mathematically:
dvdt=at=a⋅v|v|
- Instantaneous Velocity (v): The velocity of the particle at a specific instant.
- Instantaneous Acceleration (a): The acceleration of the particle at a specific instant.
The rate of change of speed is defined as:
dvdt
This represents how quickly the speed of the particle is changing over time.
The rate of change of speed is associated with the tangential component of acceleration (at), which is the component of acceleration that acts in the direction of the velocity. Therefore, we can express this as:
dvdt=at
The total acceleration a can be resolved into two components:
1. Tangential Acceleration (at): This is the component of acceleration in the direction of the velocity.
2. Normal Acceleration (an): This is the component of acceleration perpendicular to the velocity.
The tangential acceleration can be calculated using the angle θ between the velocity vector v and the acceleration vector a:
at=acos(θ)
Alternatively, using the dot product:
at=a⋅v|v|
where a⋅v is the dot product of the acceleration and velocity vectors.
Thus, we can conclude that the rate of change of speed dvdt is equal to the tangential component of acceleration, which can be expressed as:
dvdt=at=a⋅v|v|
The rate of change of speed dvdt of the particle is equal to the component of acceleration parallel to the velocity, or mathematically:
dvdt=at=a⋅v|v|
Topper's Solved these Questions
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - COMPREHENSION_TYPE
19 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - MATCH THE COLUMN
10 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
Similar Questions
Knowledge Check
A particle moves in a plane with a constant acceleration in a direction different from the initial velocity. The path of the particle is
Astraight lineBarc of circleCparabolaDellipse
Acceleration of particle moving in straight line can be written as a=dvdt=vdvdx. From the given graph find acceleration at x=20m.

View SolutionA particle is moving with a constant acceleration →a=ˆi−2ˆjm/s2 and instantaneous velocity →v=ˆi+2ˆj+2ˆkm/s then rate of change of speed of particle 1 second after this instant will be :
View SolutionThe speed of a particle moving in a circle is increasing. The dot product of its acceleration and velocity is
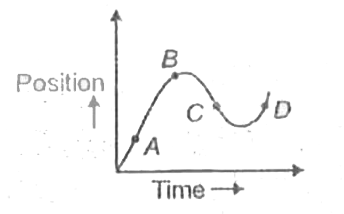
View SolutionThe position- time graph of a moving particle is shown. The instantaneous velocity of the particle is negative at the point
View SolutionAssertion: The average velocity of a particle is zero in a time interval. It is possible that the instantaneous acceleration is never zero in the interval.
Reason: The magnitude of average velocity in an interval is equal to its average speed in that interval.
View SolutionA particle moves in straight line. Acceleration of particle changes with velocity as showns in graph:

View SolutionA particle is moving with a constant acceleration →a=ˆi−2ˆj+2ˆkm/s2 and instantaneous velocity →v=ˆi+2ˆj+2ˆkm/s, then rate of change of speed of particle 2 second after this instant will be :
View Solution
