What are the forces acting on the disc?
To analyze the forces acting on a disc, we can break down the problem into several steps:
1. Identify the Disc and Its Properties:
- Consider a disc resting on a surface. The disc has a certain mass (m) and radius (r).
2. Force Due to Gravity:
- The weight of the disc acts downwards due to gravity. This force can be calculated using the formula:
Fgravity=mg
- Here, g is the acceleration due to gravity (approximately 9.81m/s2).
3. Normal Force:
- The disc is resting on a surface, which exerts an upward force known as the normal force (N). According to Newton's third law, this force balances the gravitational force when the disc is at rest:
N=mg
4. Frictional Force:
- If the disc is subjected to an external force that tends to move it, a frictional force (F) will act opposite to the direction of the applied force. The magnitude of the frictional force can be expressed as:
F=μN
- Here, μ is the coefficient of friction between the disc and the surface.
5. Torque and Radial Force (if rotating):
- If the disc is rotating, a torque (τ) is generated. The torque can be related to the moment of inertia (I) and angular acceleration (α) of the disc:
τ=Iα
- The radial force comes into play during rotation, which is related to the centripetal force required to keep the disc moving in a circular path.
6. Conclusion:
- In summary, the forces acting on the disc include:
- The gravitational force (mg) acting downwards.
- The normal force (N) acting upwards.
- The frictional force (F) acting horizontally, if applicable.
- If the disc is rotating, the torque (τ) and radial forces are also considered.
Summary of Forces:
- Downward Force: mg (Weight)
- Upward Force: N (Normal Force)
- Horizontal Force: F (Frictional Force)
- Rotational Forces: τ (Torque) and radial forces if applicable.
---
- Consider a disc resting on a surface. The disc has a certain mass (m) and radius (r).
- The weight of the disc acts downwards due to gravity. This force can be calculated using the formula:
Fgravity=mg
- Here, g is the acceleration due to gravity (approximately 9.81m/s2).
- The disc is resting on a surface, which exerts an upward force known as the normal force (N). According to Newton's third law, this force balances the gravitational force when the disc is at rest:
N=mg
- If the disc is subjected to an external force that tends to move it, a frictional force (F) will act opposite to the direction of the applied force. The magnitude of the frictional force can be expressed as:
F=μN
- Here, μ is the coefficient of friction between the disc and the surface.
- If the disc is rotating, a torque (τ) is generated. The torque can be related to the moment of inertia (I) and angular acceleration (α) of the disc:
τ=Iα
- The radial force comes into play during rotation, which is related to the centripetal force required to keep the disc moving in a circular path.
- In summary, the forces acting on the disc include:
- The gravitational force (mg) acting downwards.
- The normal force (N) acting upwards.
- The frictional force (F) acting horizontally, if applicable.
- If the disc is rotating, the torque (τ) and radial forces are also considered.
- Downward Force: mg (Weight)
- Upward Force: N (Normal Force)
- Horizontal Force: F (Frictional Force)
- Rotational Forces: τ (Torque) and radial forces if applicable.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - J) Aakash Challengers Questions13videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))5videos
SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE21videos
TEST 1
Similar Questions
A disc of mass m has a charge Q distributed on its surface. It is rotating about an XX' with a angular velocity ω. The force acting on the disc is
 View Solution
View SolutionA disc and a solid sphere of same mass and radius roll down an inclined plane. The ratio of thhe friction force acting on the disc and sphere is
View SolutionList all the forces acting on the block B in figure.
 View Solution
View SolutionCalculate the net force acting on the charge present at the origin.
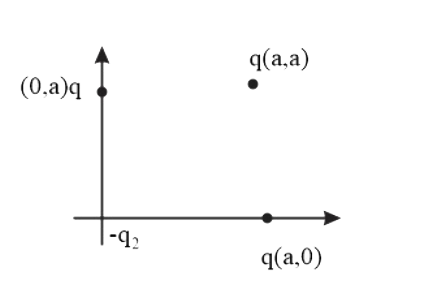 View Solution
View SolutionConsider a disc of mass m and radius R placed on a rough plank of mass M which is turn is place on a smooth horizontal surface. Now plank is pulled by a force F and disc starts to roll on the plank.
If there is no friction any where then find
(a) Fricition force acting on the disc
(b) Angular acceleration of the disc
 View Solution
View SolutionA uniform disc of mass m and radius R is rolling up a rough inclined plane which makes an angle of 30∘ with the horizontal. If the coefficients of static and kinetic friction are each equal to μ and the only force acting are gravitational and frictional, then the magnitude of the frictional force acting on the disc is and its direction is .(write up or down) the inclined plane.
View SolutionA force (ˆi−2ˆj+3ˆk) acts on a particle lying at origin. What is the torque acting on the particle about the origin.
View SolutionA force (ˆi−2ˆj+3ˆk) acts on a particle lying at origin. What is the torque acting on the particle about origin?
View SolutionPassage VIII A disc of mass m and radius R is attached with a spring of force contant k at its center as shown in figure. At x-0, spring is unstretched. The disc is moved to x=A and then released. There is no slipping between disc and ground. Let f be the force of friction on the disc from the ground.

f versus t (time) graph will be asView SolutionOne of the forces acting on the particle is conservative, then
View Solution

