The electric field due to uniformly charged sphere of radius R as a function of the distance from its centre is represented graphically by
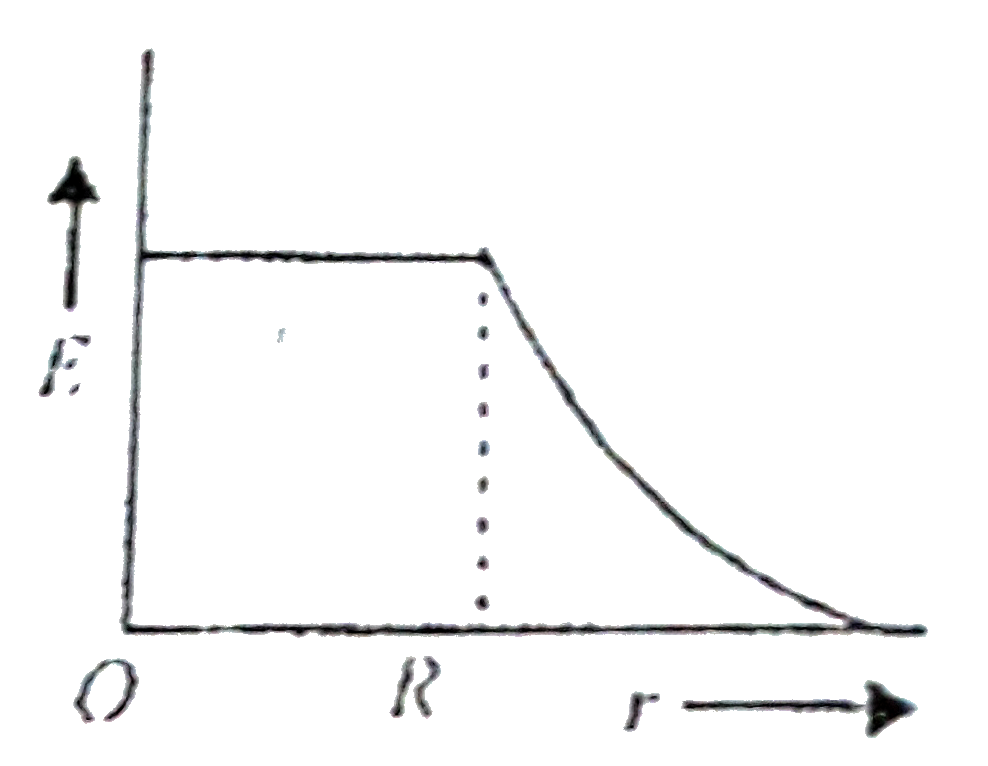
The correct Answer is:B
To solve the problem of determining the electric field due to a uniformly charged sphere of radius R as a function of the distance from its center, we can break it down into two regions: inside the sphere (when the distance x<R) and outside the sphere (when the distance x≥R).
1. Understanding the Problem:
- We have a uniformly charged sphere with total charge Q and radius R.
- We need to find the electric field E at a distance x from the center of the sphere.
2. Electric Field Inside the Sphere (x<R):
- According to Gauss's law, the electric field inside a uniformly charged sphere is given by:
E=Q⋅x4πϵ0R3
- Here, ϵ0 is the permittivity of free space.
- This can be rewritten as:
E∝x
- This indicates that the electric field inside the sphere increases linearly with distance from the center.
3. Electric Field Outside the Sphere (x≥R):
- For points outside the sphere, the electric field behaves as if all the charge were concentrated at the center of the sphere. Thus, the electric field is given by:
E=Q4πϵ0x2
- This can be rewritten as:
E∝1x2
- This indicates that the electric field decreases with the square of the distance from the center.
4. Graphical Representation:
- For x<R, the electric field E increases linearly, which can be represented as a straight line starting from the origin (0,0).
- For x≥R, the electric field E decreases as 1x2, which creates a curve that approaches the x-axis but never touches it as x tends to infinity.
5. Conclusion:
- The graph of the electric field E as a function of distance x from the center of the sphere will show a straight line for 0<x<R and a curve for x≥R that approaches zero as x increases.
Final Answer:
The correct graphical representation of the electric field due to a uniformly charged sphere of radius R as a function of the distance from its center is option B.
- We have a uniformly charged sphere with total charge Q and radius R.
- We need to find the electric field E at a distance x from the center of the sphere.
- According to Gauss's law, the electric field inside a uniformly charged sphere is given by:
E=Q⋅x4πϵ0R3
- Here, ϵ0 is the permittivity of free space.
- This can be rewritten as:
E∝x
- This indicates that the electric field inside the sphere increases linearly with distance from the center.
- For points outside the sphere, the electric field behaves as if all the charge were concentrated at the center of the sphere. Thus, the electric field is given by:
E=Q4πϵ0x2
- This can be rewritten as:
E∝1x2
- This indicates that the electric field decreases with the square of the distance from the center.
- For x<R, the electric field E increases linearly, which can be represented as a straight line starting from the origin (0,0).
- For x≥R, the electric field E decreases as 1x2, which creates a curve that approaches the x-axis but never touches it as x tends to infinity.
- The graph of the electric field E as a function of distance x from the center of the sphere will show a straight line for 0<x<R and a curve for x≥R that approaches zero as x increases.
The correct graphical representation of the electric field due to a uniformly charged sphere of radius R as a function of the distance from its center is option B.
Similar Questions
The largest magnitude the electric field on the axis of a uniformly charged ring of radius 3m is at a distance h from its centre. What is the value of h? (Take 1√2=0.7)
View SolutionIf the potential at the centre of a uniformly charged hollow sphere of radius R is V, then electric field at a distance r from the centre of sphere will be (r>R).

View SolutionThe electric potential due to uniformly charged sphere of radius R,having volume charge density rho having a spherical cavity of radius R2 as shown as in figure at point p is
_PHY_E05_288_Q01.png)
View SolutionUsing Gauss' law deduce the expression for the electric field due to a uniformly charged sperical conducting shell of radius R at a point (i) outside and (ii) inside the shell.
Plot a graph showing variation of electric field as a function of r>Randr<R. (r being the distance from the centre of the shell)
View SolutionThe electrostatic potential of a uniformly charged thin spherical shell of charge Q and radius R at a distance r from the centre
View SolutionVariation of electric potential due to npn-conducting (positively charged) solid sphere with distance from its centre is best represented as
View SolutionAssertion: Electric potential on the surface of a charged sphere of radius R is V. Then electric field at distance r=R2 from centre is V2R. Charge is distributed uniformly over the volume.
Reason: From centre to surface, electric field varies linearly with r. Here r is distance from centre.
View SolutionIn a uniformly charged sphere of total charge Q and radius R, the electric field E is plotted as function of distance from the centre, The graph which would correspond to the above will be:
View SolutionThe electric field at 2R from the centre of a uniformly charged non - conducting sphere of rarius R is E. The electric field at a distance R2 from the centre will be
View SolutionFind the electric field at the centre of a uniformly charged semicircular ring of radius R. Linear charge density is λ
View Solution