The length of a metal wire is when the tension in it is and is when the tension is . The natural length of the wire is
To find the natural length of the metal wire when given its lengths under different tensions, we can follow these steps:
1. Define Variables:
Let:
- L = natural length of the wire
- L1 = length of the wire under tension T1
- L2 = length of the wire under tension T2
- A = cross-sectional area of the wire
- Y = Young's modulus of the material of the wire
2. Calculate Change in Length:
When the tension T1 is applied, the change in length ΔL1 can be expressed as:
ΔL1=T1⋅LA⋅Y
Therefore, the length L1 can be written as:
L1=L+ΔL1=L+T1⋅LA⋅Y
This simplifies to:
L1=L(1+T1A⋅Y)
3. Repeat for Tension T2:
Similarly, for tension T2:
ΔL2=T2⋅LA⋅Y
Thus, the length L2 is:
L2=L+ΔL2=L+T2⋅LA⋅Y
This simplifies to:
L2=L(1+T2A⋅Y)
4. Set Up the Equations:
Now we have two equations:
L1=L(1+T1A⋅Y)(1)
L2=L(1+T2A⋅Y)(2)
5. Divide the Equations:
Dividing equation (1) by equation (2):
L1L2=1+T1A⋅Y1+T2A⋅Y
6. Cross Multiply:
Cross multiplying gives:
L1(1+T2A⋅Y)=L2(1+T1A⋅Y)
7. Rearranging:
Rearranging this equation leads to:
L1+L1T2A⋅Y=L2+L2T1A⋅Y
8. Isolate Terms:
Isolating terms involving A⋅Y:
L1T2−L2T1A⋅Y=L2−L1
9. Solve for A⋅Y:
Thus, we find:
A⋅Y=L1T2−L2T1L1−L2
10. Substitute Back to Find L:
Substitute A⋅Y back into either equation (1) or (2) to find L:
L=L1⋅(L2T1−L1T2)L2T1−L1T2+L1(L1−L2)
11. Final Expression:
The natural length L can be expressed as:
L=L2T1−L1T2T1−T2
Let:
- L = natural length of the wire
- L1 = length of the wire under tension T1
- L2 = length of the wire under tension T2
- A = cross-sectional area of the wire
- Y = Young's modulus of the material of the wire
When the tension T1 is applied, the change in length ΔL1 can be expressed as:
ΔL1=T1⋅LA⋅Y
Therefore, the length L1 can be written as:
L1=L+ΔL1=L+T1⋅LA⋅Y
This simplifies to:
L1=L(1+T1A⋅Y)
Similarly, for tension T2:
ΔL2=T2⋅LA⋅Y
Thus, the length L2 is:
L2=L+ΔL2=L+T2⋅LA⋅Y
This simplifies to:
L2=L(1+T2A⋅Y)
Now we have two equations:
L1=L(1+T1A⋅Y)(1)
L2=L(1+T2A⋅Y)(2)
Dividing equation (1) by equation (2):
L1L2=1+T1A⋅Y1+T2A⋅Y
Cross multiplying gives:
L1(1+T2A⋅Y)=L2(1+T1A⋅Y)
Rearranging this equation leads to:
L1+L1T2A⋅Y=L2+L2T1A⋅Y
Isolating terms involving A⋅Y:
L1T2−L2T1A⋅Y=L2−L1
Thus, we find:
A⋅Y=L1T2−L2T1L1−L2
Substitute A⋅Y back into either equation (1) or (2) to find L:
L=L1⋅(L2T1−L1T2)L2T1−L1T2+L1(L1−L2)
The natural length L can be expressed as:
L=L2T1−L1T2T1−T2
Similar Questions
Knowledge Check
The length of a rubber cord is l1 m when the tension is 4 N and l2 m when the tension is 6 N.The length when the tension is 9 N, is
A(2.5l2−1.5l1)mB(6l2−1.5l1)mC(3l1−l2)mD(3.5l2=−2.5l1)m
The length of a metal wire is l1 when the tension in it is F1 and l2 when the tension becomes F2. Find the natural length of wire.
View SolutionThe length of a steel wire is l1 when the stretching force is T1 and l2 when the stretching force is T2. The natural length of the wire is
View SolutionWhen the tension in a metal wire is T1, its length is I1. When the tension is T2, its length is I2. The natural length of wire is
View SolutionThe length of an elastic string is Xm when the tension is 8 N, and Y m when the tension is 10 N. The length in metres when the tension is 18 N is
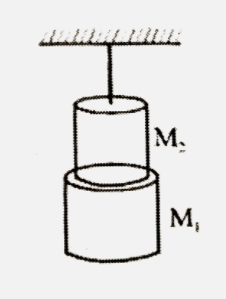
View SolutionThe length of wire, when M1 is hung from it, is l1 and is l2 with both M1 and M2 hanging. The natural length of wire is :-
View Solutionan elastic spring has a length l1 when tension in it is 4N. Its length is l2 when tension in it is 5N. What will be its length when tension in it is 9N?
View SolutionA transverse wave travels on a taut steel wire with a velocity of when tension in it is 2.06×104N . When the tension is changed to T, the velocity changed to 3v. The value of T is close to :
View Solution