Two wires one of copper and other of iron having same cross-section area and lengths 2 m and 1.5 m respectively are fastened end and stretched by a load 10 N. If copper wire is stretched by 2mm then find the total extension of combined wire, YCu=1×1011N/m2 and YFe=3×1011N/m2.
The correct Answer is:2.5 mm
To solve the problem, we need to find the total extension of two wires (one copper and one iron) when they are stretched by a load of 10 N. We are given the Young's modulus for both materials, their lengths, and the extension of the copper wire.
1. Understand Young's Modulus:
Young's modulus (Y) is defined as the ratio of stress to strain. Mathematically, it can be expressed as:
Y=StressStrain=F/AΔL/L
where:
- F = Force applied
- A = Cross-sectional area
- ΔL = Change in length (extension)
- L = Original length
2. Set Up the Equations:
For the copper wire:
YCu=F⋅LCuA⋅ΔLCu
For the iron wire:
YFe=F⋅LFeA⋅ΔLFe
3. Given Values:
- YCu=1×1011N/m2
- YFe=3×1011N/m2
- LCu=2m
- LFe=1.5m
- F=10N
- ΔLCu=2mm=2×10−3m
4. Calculate the Extension in Iron Wire:
From the equations for Young's modulus, we can express the extensions in terms of the known values. Rearranging the equation for iron:
ΔLFe=F⋅LFeYFe⋅A
We can also relate the two equations by dividing them:
YCuYFe=LCu⋅ΔLFeLFe⋅ΔLCu
Rearranging gives:
ΔLFe=YCuYFe⋅LFeLCu⋅ΔLCu
5. Substituting Known Values:
Substituting the known values into the equation:
ΔLFe=1×10113×1011⋅1.52⋅(2×10−3)
Simplifying:
ΔLFe=13⋅1.52⋅(2×10−3)
ΔLFe=1.5×2×10−36=3×10−36=0.5×10−3m=0.5mm
6. Calculate Total Extension:
Now, we can find the total extension:
ΔLtotal=ΔLCu+ΔLFe=2mm+0.5mm=2.5mm
Final Answer:
The total extension of the combined wire is 2.5mm.
Young's modulus (Y) is defined as the ratio of stress to strain. Mathematically, it can be expressed as:
Y=StressStrain=F/AΔL/L
where:
- F = Force applied
- A = Cross-sectional area
- ΔL = Change in length (extension)
- L = Original length
For the copper wire:
YCu=F⋅LCuA⋅ΔLCu
For the iron wire:
YFe=F⋅LFeA⋅ΔLFe
- YCu=1×1011N/m2
- YFe=3×1011N/m2
- LCu=2m
- LFe=1.5m
- F=10N
- ΔLCu=2mm=2×10−3m
From the equations for Young's modulus, we can express the extensions in terms of the known values. Rearranging the equation for iron:
ΔLFe=F⋅LFeYFe⋅A
We can also relate the two equations by dividing them:
YCuYFe=LCu⋅ΔLFeLFe⋅ΔLCu
Rearranging gives:
ΔLFe=YCuYFe⋅LFeLCu⋅ΔLCu
Substituting the known values into the equation:
ΔLFe=1×10113×1011⋅1.52⋅(2×10−3)
Simplifying:
ΔLFe=13⋅1.52⋅(2×10−3)
ΔLFe=1.5×2×10−36=3×10−36=0.5×10−3m=0.5mm
Now, we can find the total extension:
ΔLtotal=ΔLCu+ΔLFe=2mm+0.5mm=2.5mm
The total extension of the combined wire is 2.5mm.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBook:AAKASH INSTITUTE ENGLISHChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:Assignment (SECTION - J)
Explore 2 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:AAKASH INSTITUTE ENGLISHChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:EXERCISE
Explore 20 Videos
- MECHANICAL PROPERTIES OF SOLIDSBook:AAKASH INSTITUTE ENGLISHChapter:MECHANICAL PROPERTIES OF SOLIDSExercise:Assignment (SECTION - H)
Explore 2 Videos
- MECHANICAL PROPERTIES OF FLUIDSBook:AAKASH INSTITUTE ENGLISHChapter:MECHANICAL PROPERTIES OF FLUIDSExercise:SECTION - J
Explore 9 Videos
- Mock test 03Book:AAKASH INSTITUTE ENGLISHChapter:Mock test 03Exercise:EXAMPLE
Explore 44 Videos
Similar Questions
A steel wire and a copper wire of equal length and equal cross- sectional area are joined end to end and the combination is subjected to a tension. Find the ratio of
copper/steel
(a) the stresses developed . In the two wires,
(b) the strains developed. (Y of steel =2×1011N/m2)
View SolutionA rigid bar of mass 15 kg is supported symmetrically by three wires, each of length 2 m. The wires at the endpoints are made of copper and the middle one is made of steel. If the tension in each wire is the same, then the diameter of copper wire to the diameter of steel wire is [Given, Ycopper=1.1×1011N m−1andYsteel=1.9×1011N m−2]
View Solution
Knowledge Check
A copper wire of length 2.4 m and a steel wire of length 1.6 m, both of diameter 3 mm, are connected end to end. When stretched by a load, the net elongation found to be 0.7 mm. The load appled is
(YCopper=1.2×1011Nm−2,Ysteel=2×1011Nm−2)A1.2×102NB1.8×102NC2.4×102ND3.2×102N
A block of weight 100 N is suspended by copper and steel wires of same cross sectional area 0.5cm2 and, length √3 m and 1m, respectively. Their other ends are fixed on a ceiling as shown in figure. The angles subtended by copper and steel wires with ceiling are 30∘and60∘, respectively. If elongation in copper wire is (ΔlC) and elongation in steel wire is (Δls), then the ratio ΔlCΔls is -
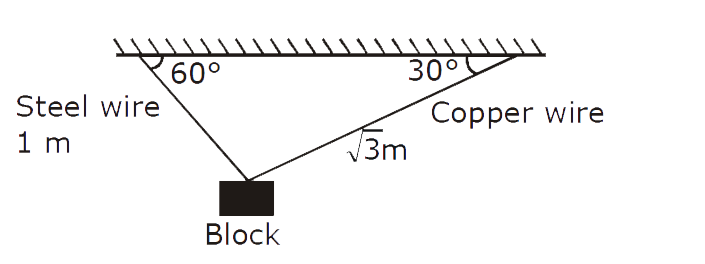
[Young's modulus for copper and steel are 1×1011N/m2and2×1011N/m2, respectively]
View SolutionA steel wire and copper wire of the same diameter and of length 1m and 2m respectively are connected end to end and a force is applied. The increase in length of the combination is 0.01m.Calculate the elongation produced in the individual wires. Given that Y of copper is 12×1010Nm2 and that of steel is 20×1010Nm−2.
View SolutionOne end of a wire 2m long and 0.2 cm^2 in cross section is fixed in a ceiling and a load of 4.8 kg is attached to the free end. Find the extension of the wire. Young modulus of steel =2.0×1011Nm−2. Take g=10ms−2.
View SolutionA steel wire and a copper wire of equal length and equal cross sectional area are joined end to end and the combination is subjected to a tension. Find the ratio of a. The stresses developed in the two wire and b. the strains developed. Y of steel =2×1011Nm−2. Y of copper =1.3×1011Nm−2.
View SolutionThe work per unit volume to stretch the length by 1% of a wire with cross sectional area of 1mm2 will be. [Y=9×1011Nm2]
View SolutionA Copper wire of length 2.2m and a steel wire of length 1.6m, both of diameter 3.0mm are connected end to end. When stretched by a load, the net elongation is found to be 0.70 mm. Obtain the load applied . Young's modulus of copper is 1.1×1011Nm−2 and Young's modulus of steel is 2.0×1011Nm−2.
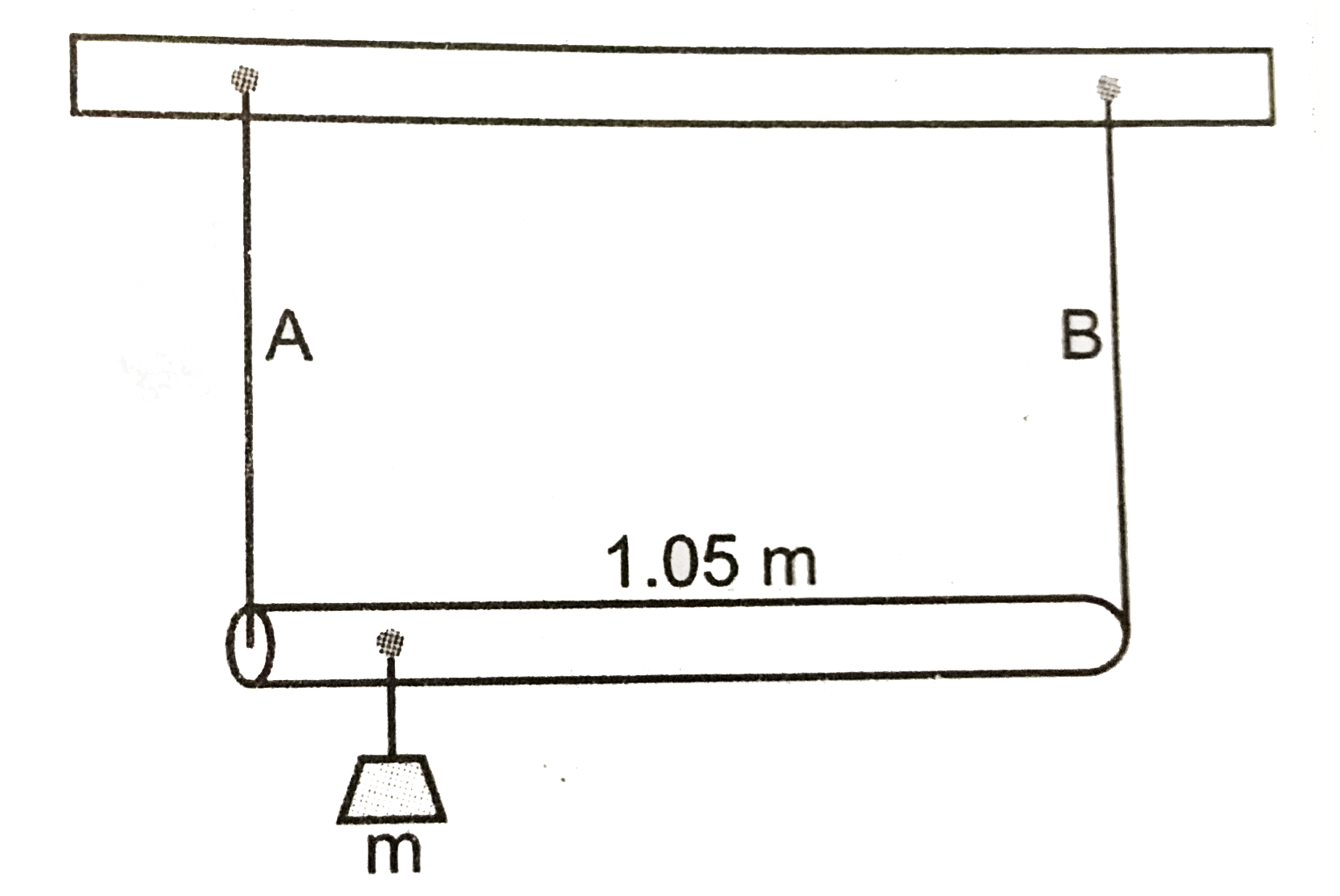
View SolutionA rod of length 1.05 m having negliaible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in fig. The cross-sectional area of wire A and B are 1mm2 and 2mm2, respectively . At what point along the rod should a mass m be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires. Given,
Ysteel=2×1011Nm−2andY−(aluminium)=7.0×1010N−2
View Solution