A manometer tube contains mercury of density kg . What difference in the levels of mercury in the two arms is indicated by a gauge pressure of ?
To solve the problem, we need to determine the difference in the levels of mercury in the two arms of the manometer due to a given gauge pressure. We can use the relationship between pressure, density, gravitational acceleration, and height difference.
1. Identify the given values:
- Density of mercury, ρ=13.6×103kg/m3
- Gauge pressure, P=1.03×105Pa
- Acceleration due to gravity, g≈10m/s2 (for simplicity)
2. Use the formula relating pressure difference and height difference:
The pressure difference due to a height difference in a fluid column is given by:
P=ρgh
where h is the height difference in meters.
3. Rearrange the formula to solve for h:
h=Pρg
4. Substitute the known values into the equation:
h=1.03×105Pa(13.6×103kg/m3)(10m/s2)
5. Calculate the denominator:
ρg=13.6×103×10=136000kg/(m2s2)=136000Pa
6. Now substitute this value back into the equation for h:
h=1.03×105136000
7. Perform the division:
h≈0.075735m
8. Convert h from meters to centimeters:
h≈0.075735×100≈7.5735cm
9. Round the answer to two decimal places:
h≈7.57cm
Final Answer:
The difference in the levels of mercury in the two arms of the manometer is approximately 7.57 cm.
- Density of mercury, ρ=13.6×103kg/m3
- Gauge pressure, P=1.03×105Pa
- Acceleration due to gravity, g≈10m/s2 (for simplicity)
The pressure difference due to a height difference in a fluid column is given by:
P=ρgh
where h is the height difference in meters.
h=Pρg
h=1.03×105Pa(13.6×103kg/m3)(10m/s2)
ρg=13.6×103×10=136000kg/(m2s2)=136000Pa
h=1.03×105136000
h≈0.075735m
h≈0.075735×100≈7.5735cm
h≈7.57cm
The difference in the levels of mercury in the two arms of the manometer is approximately 7.57 cm.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - A
50 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - B
23 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - J
9 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment(Section-D)
14 Videos
Similar Questions
A manometer tube contains a liquid of density 4×103kgm−3. When connected to a vessel containing a gas, the liquid level in the other arm of the tube is higher by 20 cm. When connected to another sample of enclosed gas, the liquid level in the other arm of the manometer tube falls 8 cm below the liquid level in the first arm. Which of the two samples exerts more pressure and by what amount ?
View SolutionA U -tube in which the cross - sectional area of the limb on the left is one quarter, the limb on the right contains mercury (density13.6g/cm3). The level of mercury in the narrow limb is at a distance of 36 cm from the upper end of the tube. What will be the rise in the level of mercury in the right limb if the left limb is filled to the top with water ?
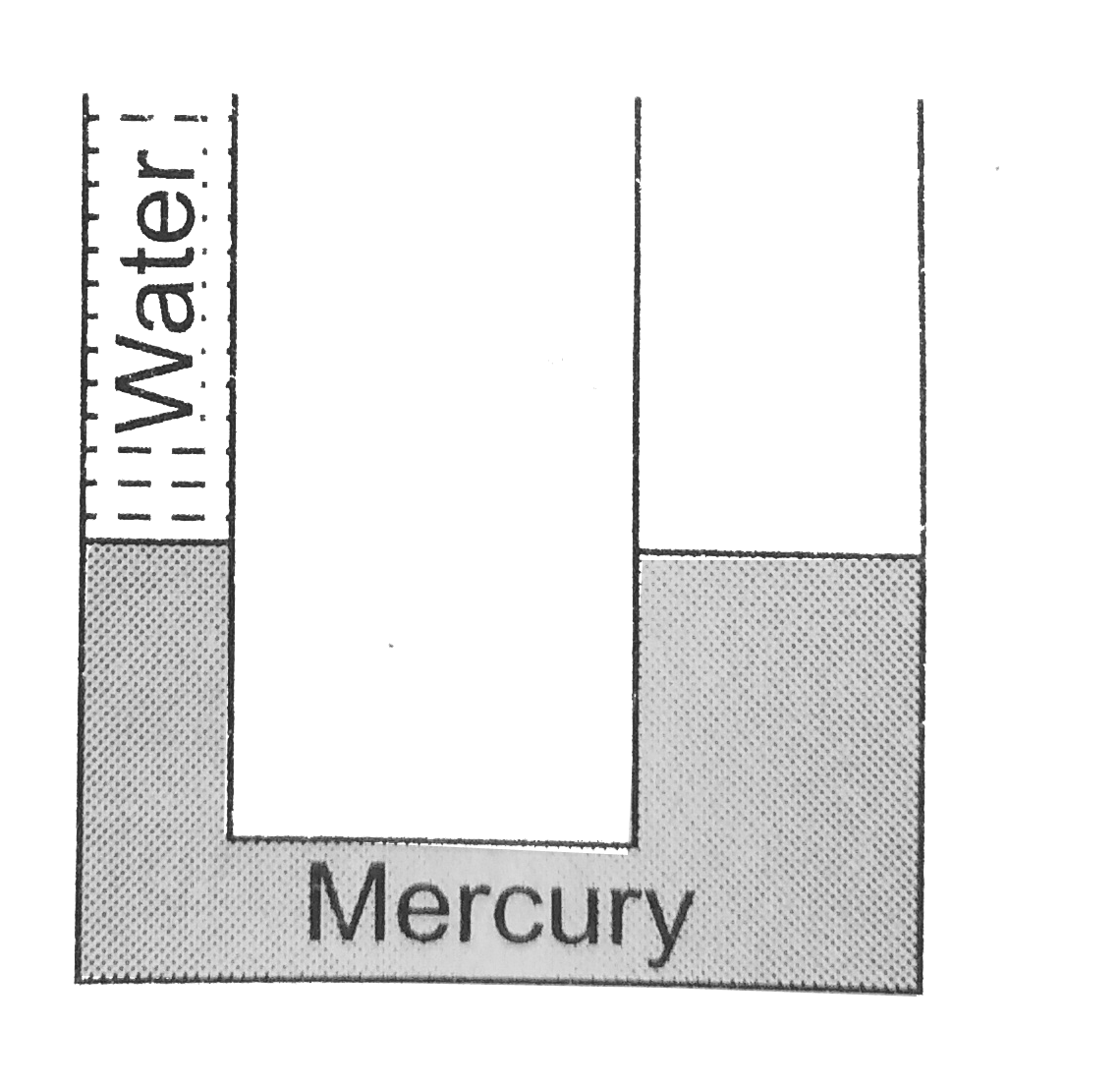
View Solution
Knowledge Check
in previous question, if 15 cm of water and spirit each are further poured into the respective arms of the tube. Difference in the level of mercury in the two arms is (Take, relvative density of mercury = 13.6)
A0.20 cmB0.22 cmC0.27 cmD0.26 cm
If 15.0 cm of water and spirit each are further poured into the respective arms of the tube, what is the difference in the levels of mercury in the two arms? (Relative density of mercury = 13.6).
View SolutionA U-tube in which the cross-sectional area of the limb on the left is one-third of the limb on the right contains mercury (density 13.6g/cm3). The level of mercury in the narrow limb extends to a distance of 30cm from the upper end of the tube. What will be the rise in the level of mercury in the right limb, if the left limb is filled to the top with water (neglect surface tension effects)?

View SolutionGlycerine flows steadily through a horizontal tube of length 1.5m and radius 1.0 cm. If the amount of glycerine collected per second at one end is4.0×10−3kgs−1 what is the pressure difference between the two ends of the tube? (Density of glycerine =1.3×103kgm−3 and coefficient of viscosity of glycerine =0.83Nsm−2)
View SolutionIn a constant volume gas thermometer, the pressure of the working gas is measured by the difference in the levels of mercury in the two arms of a U-tube connected to the gas at one end. When the bulb is placed at the room temperature 27.00C, the mercury column in the arm open to atmosphere stands 5.00cm above the level of mercury in the other arm. When the bulb is placed in a hot liquid, the difference of mercury levels becomes 45.0cm. Calculate the temperature of the liquid. (Atmospheric pressure =75.0cm of mercury).
View SolutionIn a constant volume gas thermometer, the pressure of the working gas is measured by the differenced in the levels of mercury in the two arms of a U-tube connected to the gas at one end. When the bulb is placed at the room temperature 27.00C, the mercury column in the arm open to atmosphere stands 5.00cm above the level of mercury in the other arm. When the bulb is placed in a hot liquid, the difference of mercury levels becomes 45..0Cm. Calculate the temperature of the liquid. (Atmospheric pressure =75.0cm of mercury).
View SolutionThe rms velocity molecules of a gas of density 4kgm−3 and pressure 1.2×105Nm−2 is
View SolutionThe rms velocity molecules of a gas of density 4kgm−3 and pressure 1.2×105Nm−2 is
View Solution
