In an arrangement similar to a hydraulic lift, the diameters of smaller and larger pistons are 1.0 cm and 3.0 cm respectively. What is the force exerted on the larger piston when a force of 10 N is applied to the smaller piston?
To solve the problem, we will use the principle of hydraulic systems, which states that the pressure exerted on a fluid in a closed system is transmitted undiminished throughout the fluid. This means that the pressure on both pistons is the same.
1. Identify the Given Values:
- Diameter of the smaller piston (d1) = 1.0 cm
- Diameter of the larger piston (d2) = 3.0 cm
- Force applied on the smaller piston (F1) = 10 N
2. Calculate the Radius of Each Piston:
- Radius of the smaller piston (r1) = d1 / 2 = 1.0 cm / 2 = 0.5 cm = 0.005 m
- Radius of the larger piston (r2) = d2 / 2 = 3.0 cm / 2 = 1.5 cm = 0.015 m
3. Calculate the Area of Each Piston:
- Area of the smaller piston (A1) = π * r1² = π * (0.005 m)² = π * 0.000025 m² = 7.85 x 10^-5 m²
- Area of the larger piston (A2) = π * r2² = π * (0.015 m)² = π * 0.000225 m² = 7.07 x 10^-4 m²
4. Use the Hydraulic Lift Principle:
- According to the principle, the pressure exerted on both pistons is equal:
F1A1=F2A2
- Rearranging gives:
F2=F1×A2A1
5. Substitute the Values:
- Now substitute the values of F1, A1, and A2:
F2=10N×7.07×10−4m²7.85×10−5m²
6. Calculate F2:
- First, calculate the ratio:
7.07×10−47.85×10−5≈9
- Now calculate F2:
F2=10N×9=90N
Final Answer:
The force exerted on the larger piston (F2) is 90 N.
---
- Diameter of the smaller piston (d1) = 1.0 cm
- Diameter of the larger piston (d2) = 3.0 cm
- Force applied on the smaller piston (F1) = 10 N
- Radius of the smaller piston (r1) = d1 / 2 = 1.0 cm / 2 = 0.5 cm = 0.005 m
- Radius of the larger piston (r2) = d2 / 2 = 3.0 cm / 2 = 1.5 cm = 0.015 m
- Area of the smaller piston (A1) = π * r1² = π * (0.005 m)² = π * 0.000025 m² = 7.85 x 10^-5 m²
- Area of the larger piston (A2) = π * r2² = π * (0.015 m)² = π * 0.000225 m² = 7.07 x 10^-4 m²
- According to the principle, the pressure exerted on both pistons is equal:
F1A1=F2A2
- Rearranging gives:
F2=F1×A2A1
- Now substitute the values of F1, A1, and A2:
F2=10N×7.07×10−4m²7.85×10−5m²
- First, calculate the ratio:
7.07×10−47.85×10−5≈9
- Now calculate F2:
F2=10N×9=90N
The force exerted on the larger piston (F2) is 90 N.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - A
50 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - B
23 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - J
9 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment(Section-D)
14 Videos
Similar Questions
Two syringes of different cross-sections (without needles) filled with water are connected with a tightly fitted rubber tube filled with water. Diameters of the smaller piston and larger piston are 1.0cm and 3.0 cm respectively.
(a) Find the force on the larger piston when a force of 10N is applied to the smaller piston.
(b) The smaller piston is paused in through 6.0 cm, much does the larger piston move out?
View SolutionTwo pistons of a hydraulic machine have diameters of 30.0 cm and 2.5 cm. What is the force exerted on the larger piston when 40 kg wt. is placed on the smaller piston? If the smaller piston moves in through 6 cm, how much does the other piston move out ?
View Solution
Knowledge Check
Two syringes of different cross-section (without needle filled with water are connected with a tightly fitted rubber tube filled with water. Diameters of the smaller piston an larger piston are 1cm and 3cm respectively. If a force of 10N is applied to the smaller piston then the force exerted on the larger piston is
A30NB60 NC90 ND100 NTwo similar triangles have perimeters in the ratio 3:5. The sides of the smaller triangle measure 3 cm, 5 cm, and 7 cmd, respectively. What is the perimeter, in centimeters, of the larger triangle?
A15B18C20D25
The pressure exerted on the smaller and the larger piston of a hydraulic machine is 15 Pa Calculate the force exerted by it on the larger piston, if the area of cross section of the larger piston is 4m2.
View SolutionIn a hydraulic machine, the two pistons are of area of cross section in the ratio 1:10. What weight force in needed on the narrow piston to overcome a force of 100 N on the wide piston?
View SolutionThe areas of two similar triangles are 169 cm2 and 121 cm2 respectively. If the longest side of the larger triangle is 26cm, what is the length of the longest side of the smaller triangle?
View SolutionThe areas of two similar triangles are 169 cm2 and 121 cm2 respectively. If the longest side of the larger triangle is 26cm, find the longest side of the smaller triangle.
View SolutionFigure shown a hydraulic press with the larger piston if diameter 35 cm at a height of 1.5 cm at a height of 1.5 m relative to the smaller piston of diameter 10cm. The mass on the smaller piston is 20 kg. What is the force exerted on the load by the larger piston? The density of oil in the press is 750kh/m3 . (Take g=9.8m/s2)
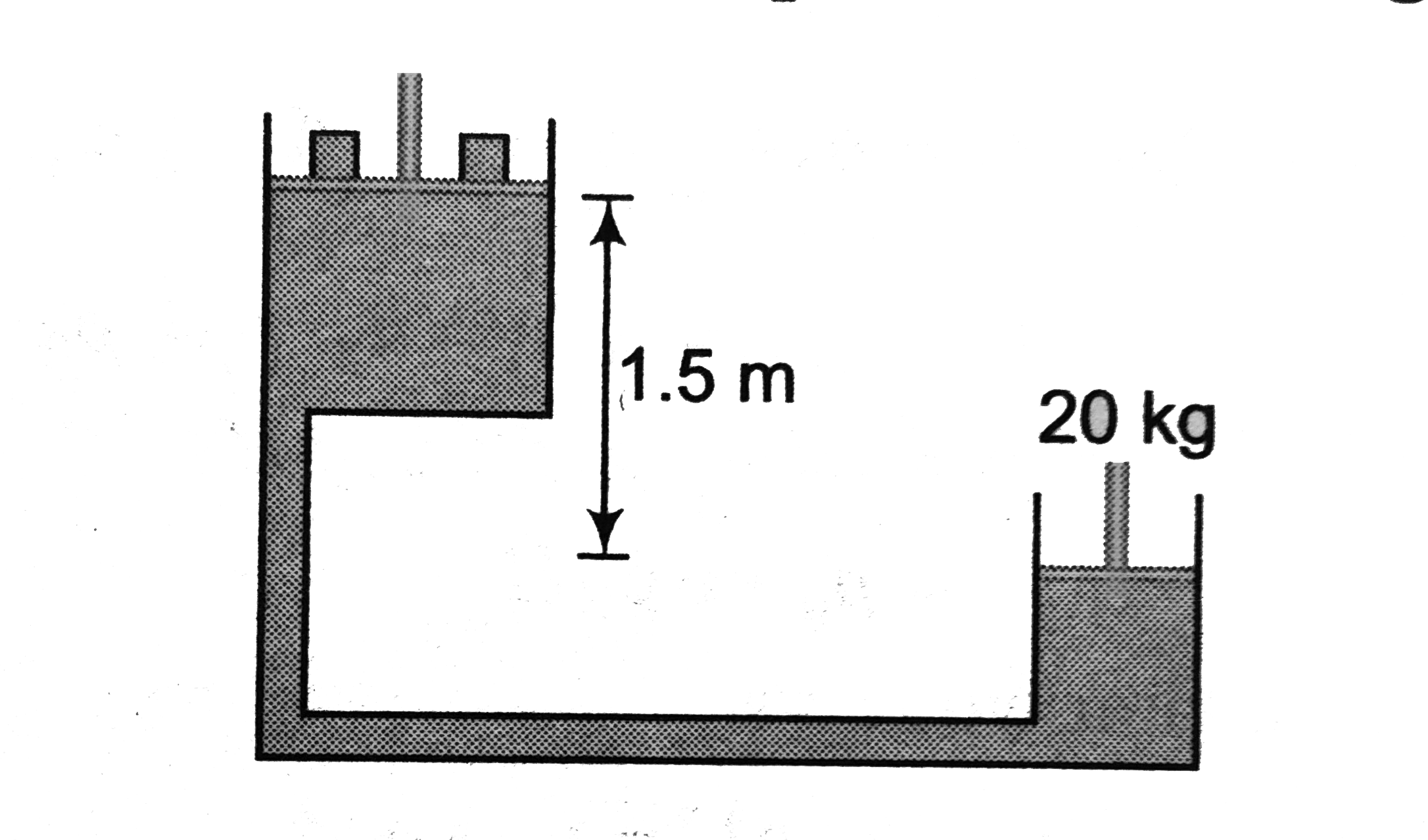 .
.
View SolutionFigure shown a hydraulic press with the larger piston if diameter 35 cm at a height of 1.5 m relative to the smaller piston of diameter 10cm. The mass on the smaller piston is 20 kg. What is the force exerted on the load by the larger piston? The density of oil in the press is 750kh/m3 . (Take g=9.8m/s2)
 .
.
View Solution
