Statement-1 : When an orifice is made in the middle of the wall of a vessel, the range of the liquid coming out of the orifice is equal to the height of the liquid.
Statement-2 : Liquid is flowing through two identical pipes A and B. Volume of liquid flowing per second through A and B are v0and2v0 respectively. Flow in A is turbulent and steady in B.
Statement-3 : Rate of flow of a viscous liquid through a pipe is directly proportional to he fourth power of the radius of pipe.
T T T
T T F
T F T
F T T
The correct Answer is:C
To analyze the three statements provided in the question, we will evaluate each statement step by step.
Statement 1:
Statement: When an orifice is made in the middle of the wall of a vessel, the range of the liquid coming out of the orifice is equal to the height of the liquid.
Solution:
1. Identify the height of the liquid (h): Let the height of the liquid in the vessel be h.
2. Determine the velocity of the liquid exiting the orifice: The velocity V of the liquid coming out of the orifice can be calculated using Torricelli’s theorem, which states:
V=√2gh
where g is the acceleration due to gravity.
3. Calculate the time taken to fall a distance h/2: The time t taken for the liquid to fall from the height h/2 to the ground can be found using the equation of motion:
s=ut+12gt2
Here, s=h2, u=0 (initial velocity), and rearranging gives:
h2=12gt2⟹t2=hg⟹t=√hg
4. Calculate the range (R): The horizontal range R can be calculated as:
R=V⋅t=√2gh⋅√hg=√2h2=h
5. Conclusion for Statement 1: The range of the liquid coming out of the orifice is indeed equal to the height of the liquid, thus Statement 1 is true.
Statement 2:
Statement: Liquid is flowing through two identical pipes A and B. Volume of liquid flowing per second through A and B are v0 and 2v0 respectively. Flow in A is turbulent and steady in B.
Solution:
1. Understand the flow characteristics: The flow in pipe A is turbulent, which typically occurs when the Reynolds number Re>4000. For pipe B, the flow is stated to be steady.
2. Relate flow rate to Reynolds number: The Reynolds number is given by:
Re=ρVDη
where V is the velocity, D is the diameter, ρ is the density, and η is the viscosity.
3. Calculate velocities for both pipes: The flow rate Q is related to the velocity V and cross-sectional area A of the pipe:
Q=A⋅V
For pipe A, let A be the area, then:
v0=A⋅VAand for pipe B,2v0=A⋅VB
This implies VB=2VA.
4. Determine the Reynolds numbers: Since the flow rate in pipe B is greater than in A, the Reynolds number for B will also be greater than that of A. Therefore, if A is turbulent, B must also be turbulent.
5. Conclusion for Statement 2: Since it is stated that flow in A is turbulent and in B is steady, this is contradictory. Thus, Statement 2 is false.
Statement 3:
Statement: Rate of flow of a viscous liquid through a pipe is directly proportional to the fourth power of the radius of the pipe.
Solution:
1. Use Poiseuille’s Law: The rate of flow Q for a viscous fluid through a pipe is given by:
Q=πr4(P1−P2)8ηL
where P1−P2 is the pressure difference, η is the viscosity, and L is the length of the pipe.
2. Identify the relationship: From the equation, we can see that the flow rate Q is proportional to r4:
Q∝r4
3. Conclusion for Statement 3: Therefore, the statement that the rate of flow of a viscous liquid through a pipe is directly proportional to the fourth power of the radius of the pipe is true.
Final Conclusion:
- Statement 1: True
- Statement 2: False
- Statement 3: True
Thus, the final answer is TFT (True, False, True).
---
Statement: When an orifice is made in the middle of the wall of a vessel, the range of the liquid coming out of the orifice is equal to the height of the liquid.
1. Identify the height of the liquid (h): Let the height of the liquid in the vessel be h.
2. Determine the velocity of the liquid exiting the orifice: The velocity V of the liquid coming out of the orifice can be calculated using Torricelli’s theorem, which states:
V=√2gh
where g is the acceleration due to gravity.
3. Calculate the time taken to fall a distance h/2: The time t taken for the liquid to fall from the height h/2 to the ground can be found using the equation of motion:
s=ut+12gt2
Here, s=h2, u=0 (initial velocity), and rearranging gives:
h2=12gt2⟹t2=hg⟹t=√hg
4. Calculate the range (R): The horizontal range R can be calculated as:
R=V⋅t=√2gh⋅√hg=√2h2=h
5. Conclusion for Statement 1: The range of the liquid coming out of the orifice is indeed equal to the height of the liquid, thus Statement 1 is true.
Statement: Liquid is flowing through two identical pipes A and B. Volume of liquid flowing per second through A and B are v0 and 2v0 respectively. Flow in A is turbulent and steady in B.
1. Understand the flow characteristics: The flow in pipe A is turbulent, which typically occurs when the Reynolds number Re>4000. For pipe B, the flow is stated to be steady.
2. Relate flow rate to Reynolds number: The Reynolds number is given by:
Re=ρVDη
where V is the velocity, D is the diameter, ρ is the density, and η is the viscosity.
3. Calculate velocities for both pipes: The flow rate Q is related to the velocity V and cross-sectional area A of the pipe:
Q=A⋅V
For pipe A, let A be the area, then:
v0=A⋅VAand for pipe B,2v0=A⋅VB
This implies VB=2VA.
4. Determine the Reynolds numbers: Since the flow rate in pipe B is greater than in A, the Reynolds number for B will also be greater than that of A. Therefore, if A is turbulent, B must also be turbulent.
5. Conclusion for Statement 2: Since it is stated that flow in A is turbulent and in B is steady, this is contradictory. Thus, Statement 2 is false.
Statement: Rate of flow of a viscous liquid through a pipe is directly proportional to the fourth power of the radius of the pipe.
1. Use Poiseuille’s Law: The rate of flow Q for a viscous fluid through a pipe is given by:
Q=πr4(P1−P2)8ηL
where P1−P2 is the pressure difference, η is the viscosity, and L is the length of the pipe.
2. Identify the relationship: From the equation, we can see that the flow rate Q is proportional to r4:
Q∝r4
3. Conclusion for Statement 3: Therefore, the statement that the rate of flow of a viscous liquid through a pipe is directly proportional to the fourth power of the radius of the pipe is true.
- Statement 1: True
- Statement 2: False
- Statement 3: True
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - I
6 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - J
9 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - SECTION - G
6 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - Assignment(Section-D)
14 Videos
Similar Questions
A device used for measuring the rate of flow of liquid through pipes is called………..
View SolutionThe volume of a liquid flowing per second out of an orifice at the bottom of a tank does not depend upon
View SolutionExplain the working of a venturimeter, Obtain an expression for the volume of liquid flowing per second through pipe.
View SolutionThe rate of flow of liquid through a capillary tube in an experiment to determine the viscosity of the liquid increases
View SolutionAn incompressible liquid is flowing through a horizontal pipe as shown in figure. The value of speed v is
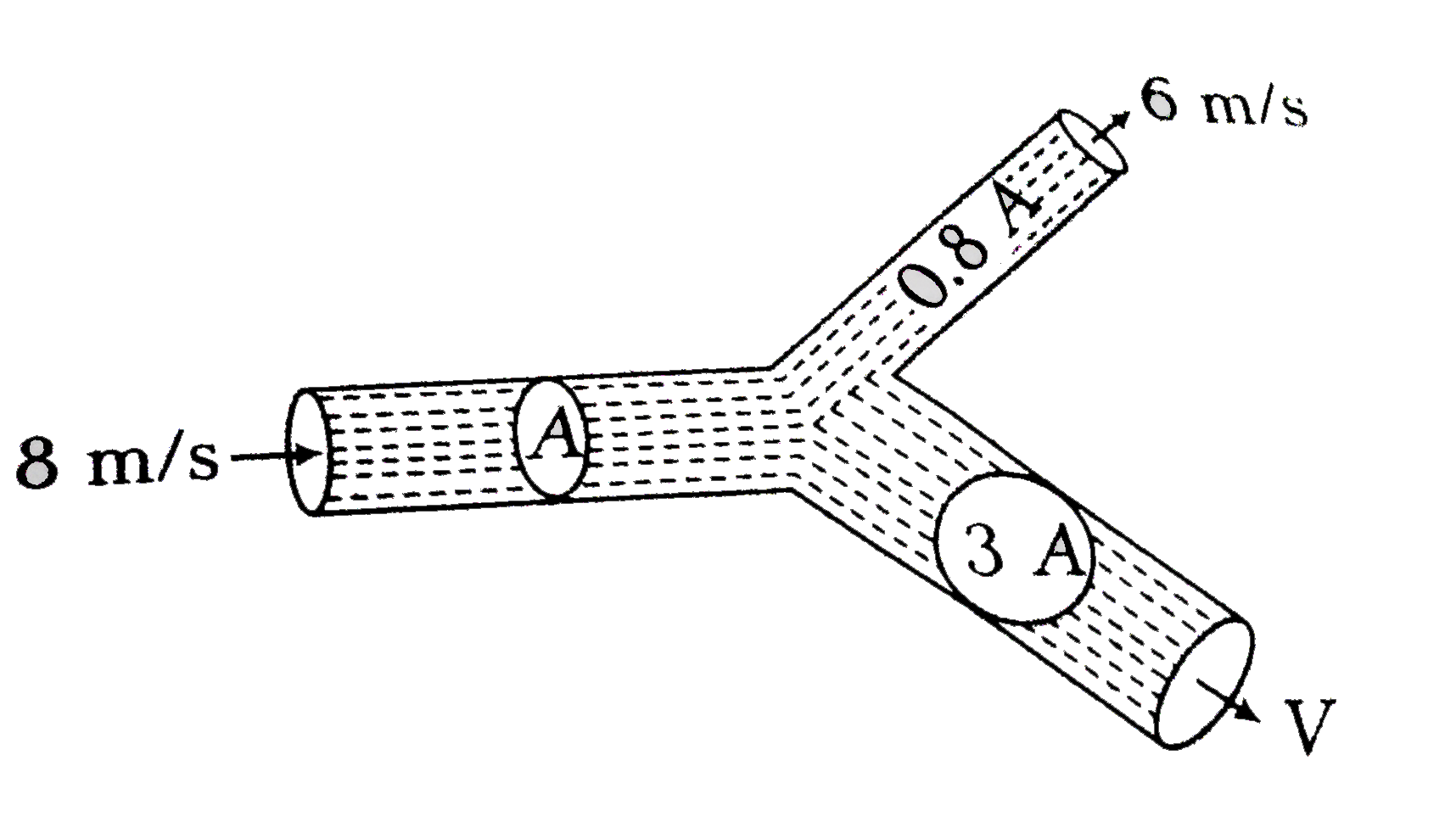
View SolutionAn incompressible liquid is flowing through a horizontal pipe as shown in figure. Find the value of v.
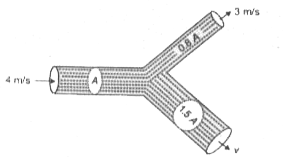
View SolutionThe velocity of efflux of a liquid through an orifice in the bottom of a tank does not depend upon
View SolutionThe steady flow of (non-viscous) liquid. Which of the two figure is incorrect?why?
View SolutionA liquid flows easily . Why ?
View SolutionWhat is laminar flow of liquid?
View Solution
