A particle moves under force F=5(x−2)3 .Motion of the particle is
Translatory
Oscillatory
SHM
All of these
The correct Answer is:2
Step by step video & image solution for A particle moves under force F =5(x -2)^(3) .Motion of the particle is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT (SECTION-B )25videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( SECTION-C )11videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - Try Yourself86videos
OSCILLATIONS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)10videos
NUCLEI
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)4videos
PHYSICAL WORLD
Similar Questions
For a particle showing motion under forces F=−5(x−2)2 , the motion is
View SolutionA particle moves under the force F(x)=(x2−6x)N, where x is in metres. For small displacements from the origin what is the force constant in the simple harmonic motion approximation ?
View SolutionFor a particle showing motion under forces F=−5(x−2) , the motion is
View SolutionA particle with total energy E is moving in a potential energy region U(x). Motion of the particle is restricted to the region when
View SolutionUnder the action of a force F=−kx3 , the motion of a particle is (k=a positive constant)
View SolutionA particle of mass 2kg is moving on a straight line under the action of force F=(8−2x)N. The particle is released at rest from x=6m. For the subsequnent motion(All the value in the right column are in their S.I. units)
_E01_071_Q01.png)
View SolutionAccording to Newton.s second law of motion, resultant force on a particle is in the direction of acceleration of the particle. Two forcce F1andF2 are acting on a particle as shown in the figure. The acceleration of the particle is along X-axis. FInd the value of F1 (in newton)
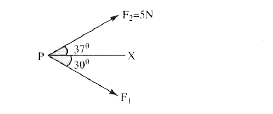
View SolutionA particle moves along x - axis under the action of a position dependent force F=(5x2−2x)N. Work done by force on the particle when it moves from origin to x = 3 m is
View SolutionThe position of a particle moving on a stringht line under rthe action of a force is given as x=50t−5t2 Here, x is in metre and t is in second. If mass of the particle is 2 kg, the work done by the force acting on the particle in first 5 s is.
View SolutionA particle moves under the action of a force F=20ˆi+15ˆj along a straight line 3y+αx=5, where, α is a constant. If the work done by the force F is zero the value of α is .
View Solution