A particle of mass 2kg is moving on a straight line under the action of force F=(8−2x)N. The particle is released at rest from x=6m. For the subsequnent motion(All the value in the right column are in their S.I. units)
_E01_071_Q01.png)
The correct Answer is:A, B, C, D
_E01_071_S01.png)
F=8−2x=−2(x−4)
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Asseration & Reason7videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Comprehension Base Questions (1)2videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise- 3 Match The Column1videos
SIMPLE HARMONIC MOTION
- BOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)24videos
RACE
- BOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS4videos
TEST PAPER
Similar Questions
A particle of mass 2kg is moving of a straight line under the action of force F=(8−2x)N. It is released at rest from x=6m.
a. Is the particle moving simple harmonically.
b. Find the equilibrium position of the particle.
c. Write the equation of motion of the particle.
d. Find the time period of SHM.View SolutionA particle of mass 2kg is moving on a straight line under the action of force F=(8−2x)N. It released at rest from x=6m.
(a) Is the particle moving simple harmonically.
(b) Find the equilibrium position of the particle.
(c) Write the equation of motionof the particle.
(d) Find the time period of SHM.View SolutionA particle of mass 2kg is moving of a straight line under the actin force F=(8−2x)N. It is released at rest from x=6m.
a. Is the partical moving simple harmonically.
b.Find the equilibrium position of the particle.
c. Write the equation of motion of the partical.
d. Find the time period of SHM.View SolutionA particle of mass 1 kg is moved under the action of a force and velocity time graph of the particle is shown in figure.Work done by the force from t=0 to t=6 s Is
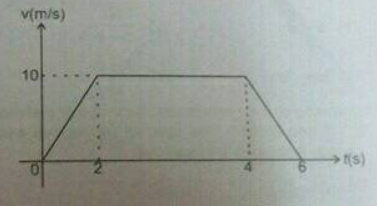View SolutionA particle of mass m moves from A to C under the action of force →F=2xyˆi+y2ˆj , along different paths as shown in figure.
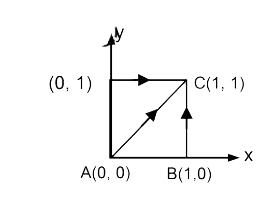View SolutionA particle of mass 2 kg starts motion at time t = 0 under the action of variable force F = 4t (where F is in N and t is in s). The work done by this force in first two second is
View SolutionA particle of mass 1kg moves from rest along a straight line due to acition of a force F which varies with the displacement x as shown in graph−( Use 1√2=0.8 if needed )
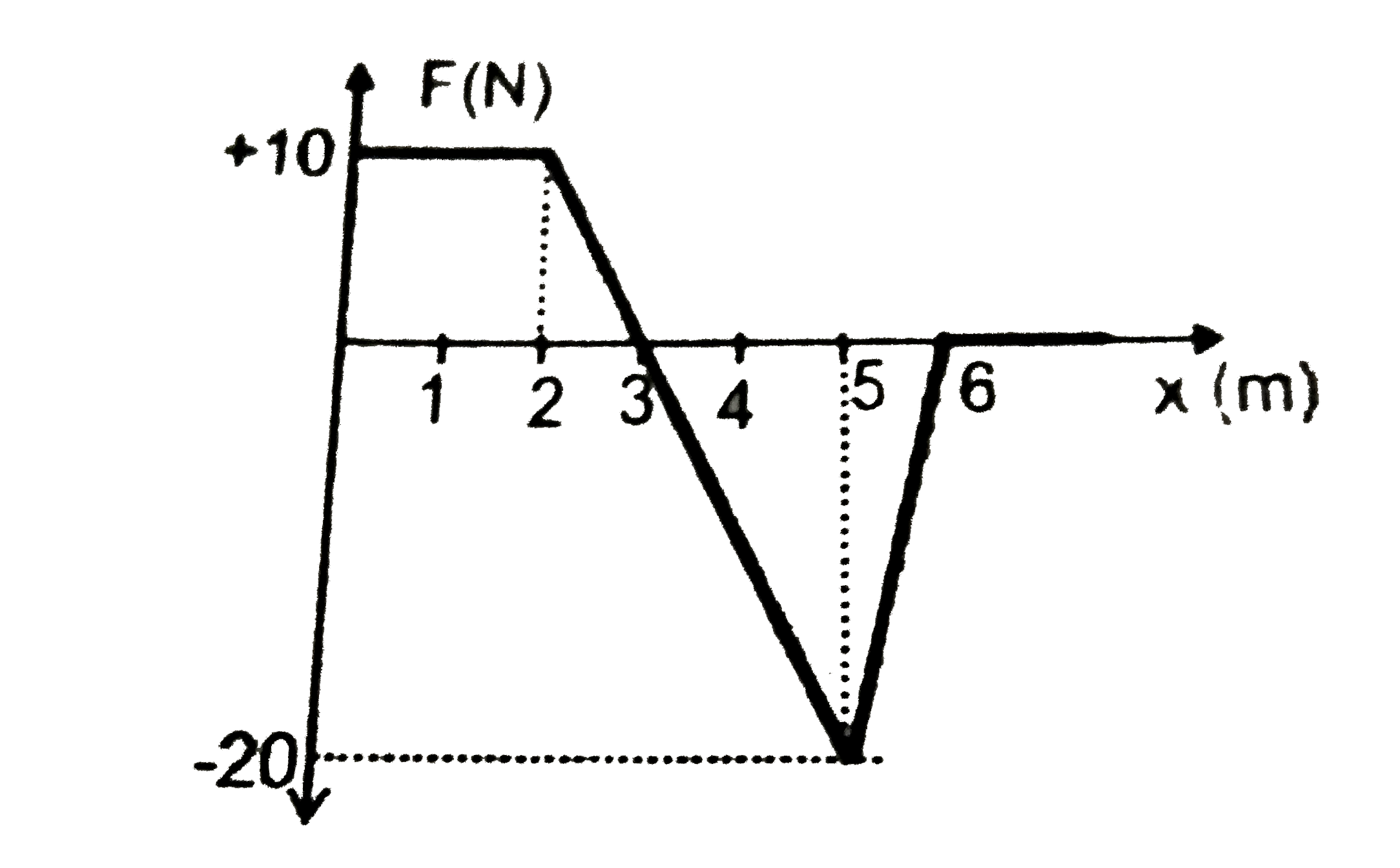View SolutionA particle moves under force F=5(x−2)3 .Motion of the particle is
View SolutionA particle of mass m moves from rest under the action of a constant force F which acts for two seconds. The maximum power attained is
View SolutionA particle of mass m moves on positive x-axis under the influence of force acting towards the origin given by −kx2ˆi. If the particle starts from rest at x=a, the speed it will attain when it crosses the origin is
View Solution