Variation of acceleration a of a particle executing SHM with displacement x is
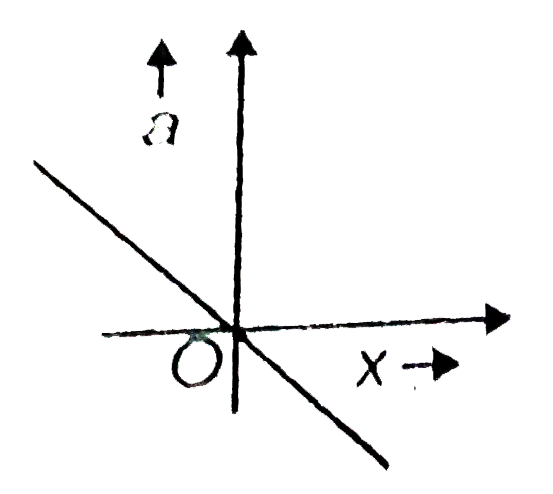
The correct Answer is:3
To solve the question regarding the variation of acceleration a of a particle executing Simple Harmonic Motion (SHM) with displacement x, we can follow these steps:
Step 1: Understand the relationship in SHM
In SHM, the displacement x of a particle can be described by the equation:
x(t)=Asin(ωt+ϕ)
where:
- A is the amplitude,
- ω is the angular frequency,
- ϕ is the phase constant.
Step 2: Derive the expression for acceleration
The acceleration a of the particle is given by the second derivative of displacement with respect to time:
a=d2xdt2
To find a, we first differentiate x(t):
v=dxdt=Aωcos(ωt+ϕ)
Now, differentiate v to find a:
a=dvdt=−Aω2sin(ωt+ϕ)
Step 3: Relate acceleration to displacement
Using the original displacement equation, we can express acceleration in terms of displacement x:
a=−ω2x
This shows that acceleration a is directly proportional to displacement x but in the opposite direction (hence the negative sign).
Step 4: Graphical representation
The equation a=−ω2x represents a straight line through the origin with a negative slope of −ω2. This means that as x increases, a decreases, and vice versa.
Conclusion
The variation of acceleration a with displacement x is a straight line passing through the origin with a negative slope.
Final Answer
The correct option is a straight line passing through the origin with a negative slope.
---
In SHM, the displacement x of a particle can be described by the equation:
x(t)=Asin(ωt+ϕ)
where:
- A is the amplitude,
- ω is the angular frequency,
- ϕ is the phase constant.
The acceleration a of the particle is given by the second derivative of displacement with respect to time:
a=d2xdt2
To find a, we first differentiate x(t):
v=dxdt=Aωcos(ωt+ϕ)
Now, differentiate v to find a:
a=dvdt=−Aω2sin(ωt+ϕ)
Using the original displacement equation, we can express acceleration in terms of displacement x:
a=−ω2x
This shows that acceleration a is directly proportional to displacement x but in the opposite direction (hence the negative sign).
The equation a=−ω2x represents a straight line through the origin with a negative slope of −ω2. This means that as x increases, a decreases, and vice versa.
The variation of acceleration a with displacement x is a straight line passing through the origin with a negative slope.
The correct option is a straight line passing through the origin with a negative slope.
Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT (SECTION-B )
25 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( SECTION-C )
11 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - Try Yourself
86 Videos
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
4 Videos
Similar Questions
Knowledge Check
If x, v and a denote the displacement, the velocity and the acceleration of a particle executing simple harmonic motion of time period T, then, which of the following does not change with time?
AaTvBaT+2πvCaTxDa2T+4π2v2A particle executing simple harmonic motion with an amplitude 5 cm and a time period 0.2 s. the velocity and acceleration of the particle when the displacement is 5 cm is
A0.5πms−1,0ms−2B0.5ms−1,−5π2ms−2C0ms−1,−5π2ms−2D0.5πms−1,−0.5π2ms−2
The graph shows the variation of displacement of a particle execting SHM with time . We infer from this graph that
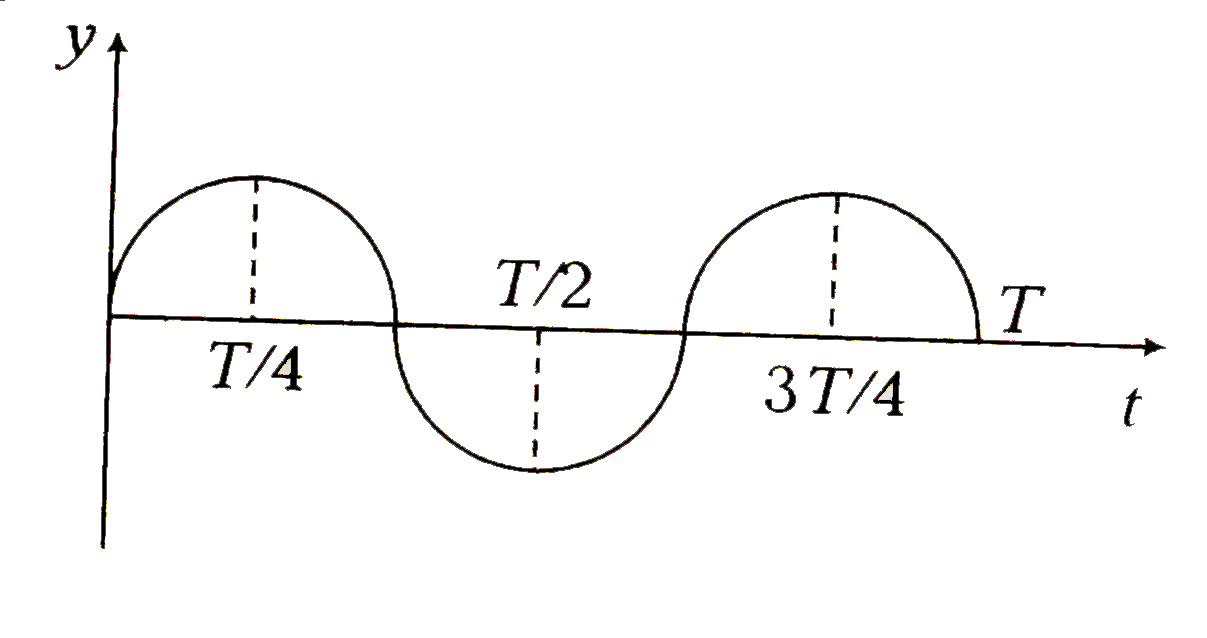
View SolutionEnergy of particle executing SHM depends upon
View SolutionThe potential energy of a particle executing S.H.M. is 2.5 J, when its displacement is half of amplitude. The total energy of the particle will be
View SolutionIf y, v and a represent displacement velocity and acceleration at any instant for a particle executing SHM, which of the following statements are true?
View SolutionIf x, v and a denote the displacement, the velocity and the acceleration of a particle executing simple harmonic motion of time period T, then, which of the following does not change with time?
View SolutionAcceleration displacement (a-x) graph of a particle executing S.H.M. is shown in the figure. The frequency of oscillation is (tanθ=8)
View Solution

_E01_037_Q01.png)