A spring of force constant 600Nm−1 is mounted on a horizontal table. A mass of 1.5 kg is attached to the free end of the spring,pulled sideways to a distance of 2 cm and released . The speed of the mass when the spring is compressed by 1 cm is
0.175ms−1
0.35ms−1
0.7ms−1
1.4ms−1
The correct Answer is:2
To solve the problem, we will use the principle of conservation of mechanical energy. The total mechanical energy in the system remains constant if only conservative forces are acting on it, such as the spring force in this case.
1. Identify Given Values:
- Force constant of the spring, k=600N/m
- Mass attached to the spring, m=1.5kg
- Initial extension (amplitude), A=2cm=0.02m
- Compression of the spring when we want to find the speed, x=−1cm=−0.01m (negative because it is a compression)
2. Calculate Initial Potential Energy (PE_initial):
The potential energy stored in the spring when it is stretched to its maximum amplitude is given by:
PEinitial=12kA2=12×600×(0.02)2
PEinitial=12×600×0.0004=0.12J
3. Calculate Final Potential Energy (PE_final):
The potential energy when the spring is compressed by 1 cm is:
PEfinal=12kx2=12×600×(0.01)2
PEfinal=12×600×0.0001=0.03J
4. Apply Conservation of Mechanical Energy:
According to the conservation of energy:
PEinitial+KEinitial=PEfinal+KEfinal
Since the mass is released from rest, KEinitial=0:
0.12+0=0.03+KEfinal
Rearranging gives:
KEfinal=0.12−0.03=0.09J
5. Calculate Final Kinetic Energy (KE_final):
The kinetic energy is given by:
KEfinal=12mv2
Substituting the known values:
0.09=12×1.5×v2
0.09=0.75v2
Solving for v2:
v2=0.090.75=0.12
Taking the square root gives:
v=√0.12≈0.346m/s
6. Final Result:
The speed of the mass when the spring is compressed by 1 cm is approximately:
v≈0.35m/s
- Force constant of the spring, k=600N/m
- Mass attached to the spring, m=1.5kg
- Initial extension (amplitude), A=2cm=0.02m
- Compression of the spring when we want to find the speed, x=−1cm=−0.01m (negative because it is a compression)
The potential energy stored in the spring when it is stretched to its maximum amplitude is given by:
PEinitial=12kA2=12×600×(0.02)2
PEinitial=12×600×0.0004=0.12J
The potential energy when the spring is compressed by 1 cm is:
PEfinal=12kx2=12×600×(0.01)2
PEfinal=12×600×0.0001=0.03J
According to the conservation of energy:
PEinitial+KEinitial=PEfinal+KEfinal
Since the mass is released from rest, KEinitial=0:
0.12+0=0.03+KEfinal
Rearranging gives:
KEfinal=0.12−0.03=0.09J
The kinetic energy is given by:
KEfinal=12mv2
Substituting the known values:
0.09=12×1.5×v2
0.09=0.75v2
Solving for v2:
v2=0.090.75=0.12
Taking the square root gives:
v=√0.12≈0.346m/s
The speed of the mass when the spring is compressed by 1 cm is approximately:
v≈0.35m/s
Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT (SECTION-B )
25 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( SECTION-C )
11 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - OSCILLATIONSEXERCISE - Try Yourself
86 Videos
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
4 Videos
Similar Questions
A spring of force constant 600Nm−1 is mounted on a horizontal table. A mass of 1.5 kg is attached to the free end of the spring, pulled sideways to a distance of 2 cm and released .P.E. of the mass when it momentarily comes to rest and total energy are
View SolutionA spring of force constant 1200Nm−1 is mounted on a horizontal table as shown in figure. A mass of 3.0kg is attached to the free end of the spring, pulled side ways to a distance of 2.0cm and released. Determing.
(a) the frequency of oscillation of the mass.
(b) the maximum acceleration of the mass.
(c) the maximum speed of the mass.

View Solution
Knowledge Check
A weightless spring of length 60 cm and force constant 100Nm−1 is kept straight and unstretched on a smooth horizontal table and its ends are rigidly fixed. A mass of 0.25 kg is attached at the middle of the spring and is slightly displaced along the length. The time period of the oscillation of the mass is
Aπ20 sBπ10 sCπ5 sDπ√200 s
A spring of force constant 1200Nm−1 is mounted on a horizontal table as shown in figure. A mass of 3.0kg is attached to the free end of the spring, pulled side ways to a distance of 2.0cm and released. Determing.
(a) the frequency of oscillation of the mass.
(b) the maximum acceleration of the mass.
(c) the maximum speed of the mass.

View SolutionA spring of force constant 1200Nm−1 is mounted on a horizontal table and a mass of 3.0 kg of attached to the free and of the spring. The mass is made to rotate with an angular velocity of 10 rad/s. What is the elongation produced in the spring if its unstretched length is 60 cm ?
View SolutionSpring of spring constant 1200Nm−1 is mounted on a smooth fricationless surface and attached to a block of mass 3kg. Block is pulled 2cm to the right and released. The angular frequency of oscillation is
_S01_037_Q01.png)
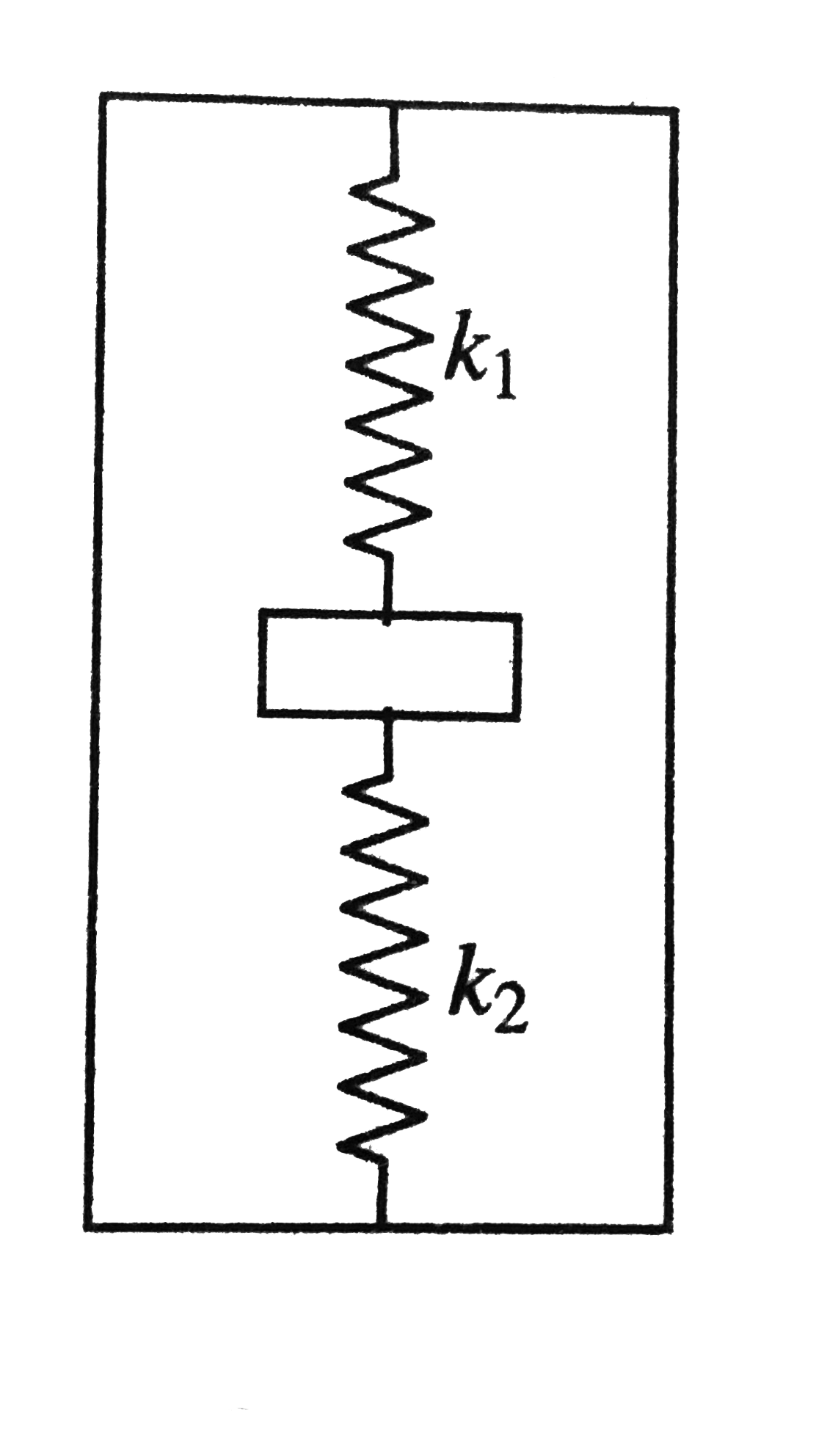
View SolutionOne end of a spring of force constant k1 is attached to the ceiling of an elevator. A block of mass 1.5kg is attached to the other end. Another spring of force constant k2 is attached to the bottom of the mass and to the floor of the elevator as shown in figure. At equilibrium, the deformation in both the spring is equal and is 40cm. If the elevator moves with constant acceleration upward, the additional deformation in both the spring is 8cm. Find the elevator's accelerationn ( g=10ms−2).
View SolutionA vertical spring with force constant k is fixed on a table. A ball of mass m at a height h above the free upper end of the spring falls vertically on the spring , so that the spring is compressed by a distance d. The net work done in the process is
View SolutionA block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
View SolutionA spring has natural length 40cm and spring constant 500N/m. A block of mass 1kg is attached at one end of the spring and other end of the spring is attached to a ceiling. The block is relesed from the position, where the spring has length 45cm.
View Solution
