For a process, relation between temperature and volume is TV3=constant. If a monoatomic gas follows this process, find molar specific heat for this process
7R6
R3
11R6
Zero
The correct Answer is:A
To find the molar specific heat for the given process where the relation between temperature and volume is TV3=constant for a monoatomic gas, we can follow these steps:
Step 1: Understand the given relation
We have the relation TV3=C, where C is a constant. This implies that as the volume changes, the temperature will also change in such a way that the product TV3 remains constant.
Step 2: Use the ideal gas law
From the ideal gas law, we know:
PV=nRT
From this, we can express temperature T in terms of pressure P and volume V:
T=PVnR
Step 3: Substitute T into the given relation
Substituting the expression for T into the relation TV3=C:
(PVnR)V3=C
This simplifies to:
PV4nR=C
Thus, we can write:
PV4=nRC
Since nR is a constant, we can denote nRC as another constant C′:
PV4=C′
Step 4: Identify the polytropic index
The equation PVn=constant indicates a polytropic process. By comparing:
PV4=C′
we see that the polytropic index n=4.
Step 5: Determine the specific heat capacity
For a polytropic process, the molar specific heat capacity C is given by:
C=Rγ−1+R1−n
For a monoatomic gas, the ratio of specific heats γ is:
γ=53
Substituting n=4 and γ=53 into the specific heat capacity formula:
C=R53−1+R1−4
Step 6: Simplify the equation
Calculating the first term:
53−1=53−33=23
Thus:
R23=3R2
Calculating the second term:
1−4=−3⇒R−3=−R3
Now combining both terms:
C=3R2−R3
Finding a common denominator (which is 6):
C=9R6−2R6=7R6
Final Answer
The molar specific heat for this process is:
C=7R6
We have the relation TV3=C, where C is a constant. This implies that as the volume changes, the temperature will also change in such a way that the product TV3 remains constant.
From the ideal gas law, we know:
PV=nRT
From this, we can express temperature T in terms of pressure P and volume V:
T=PVnR
Substituting the expression for T into the relation TV3=C:
(PVnR)V3=C
This simplifies to:
PV4nR=C
Thus, we can write:
PV4=nRC
Since nR is a constant, we can denote nRC as another constant C′:
PV4=C′
The equation PVn=constant indicates a polytropic process. By comparing:
PV4=C′
we see that the polytropic index n=4.
For a polytropic process, the molar specific heat capacity C is given by:
C=Rγ−1+R1−n
For a monoatomic gas, the ratio of specific heats γ is:
γ=53
Substituting n=4 and γ=53 into the specific heat capacity formula:
C=R53−1+R1−4
Calculating the first term:
53−1=53−33=23
Thus:
R23=3R2
Calculating the second term:
1−4=−3⇒R−3=−R3
Now combining both terms:
C=3R2−R3
Finding a common denominator (which is 6):
C=9R6−2R6=7R6
The molar specific heat for this process is:
C=7R6
Topper's Solved these Questions
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Assignment (Section-C) Objective Type Questions (More than one option are correct)
11 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Assignment (Section-D) Linked comprehension Type questions
3 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Assignment (Section-A) Objective Type Questions (one option is correct)
50 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assignment (Section-J) Akash Challengers Questions
7 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
Similar Questions
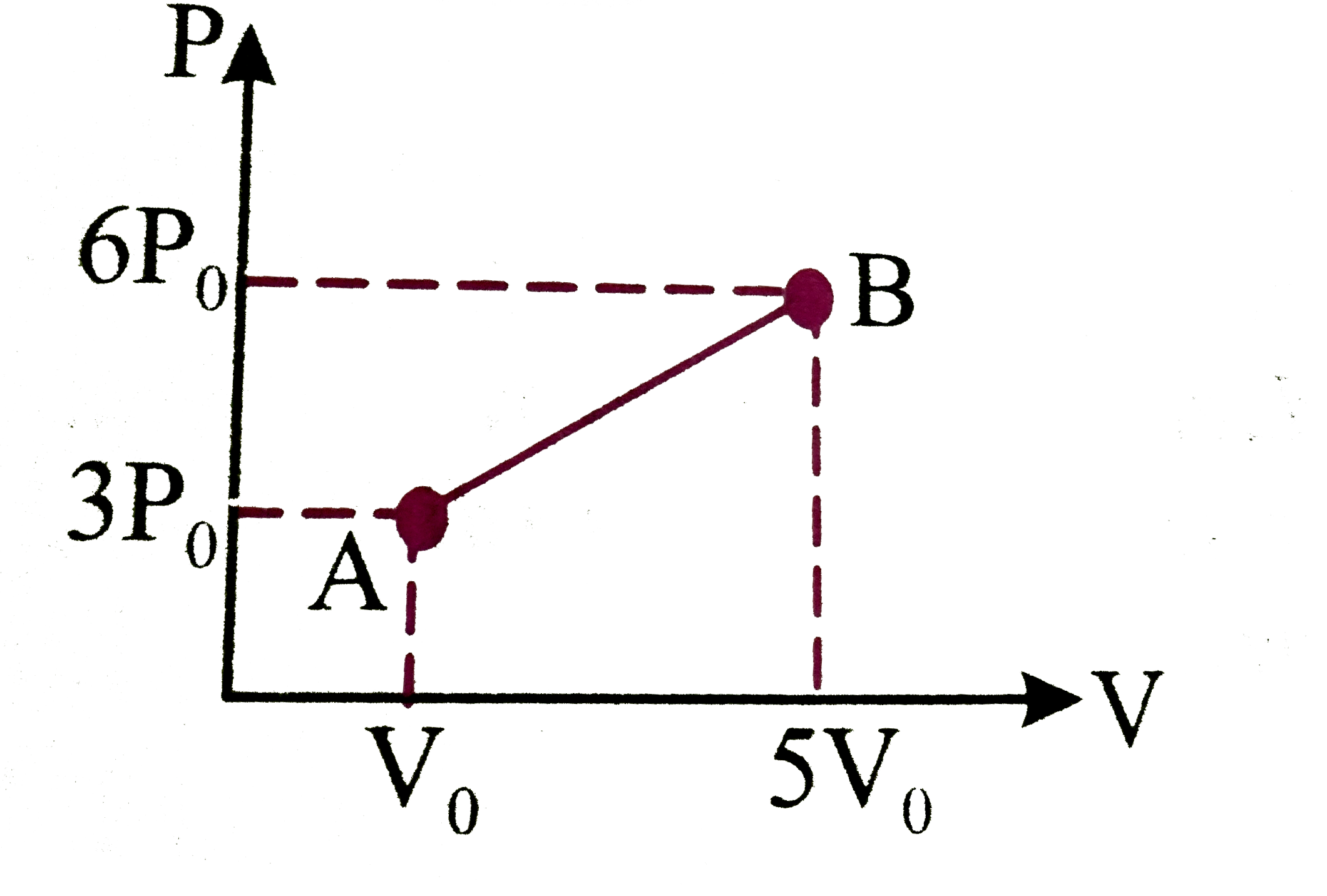
One mole of a monoatomic ideal gas undergoes the process A→B in the given P-V diagram. What is the specific heat for this process?
View SolutionA monoatomic gas undergoes a process in which the pressure (P) and the volume (V) of the gas are related as PV−3=constant. What will be the molar heat capacity of gas for this process?
View SolutionIn a process, temperature and volume of one mole of an ideal monoatomic gas are varied according to the relation VT= K, where K is a constant. In this process the temperataure of the gas is increased by ΔT. The amount of heat absorbed by gas is (R is gas constant).
View SolutionIn a process, temperature and volume of one mole of an ideal monoatomic gas are varied according to the relation VT= K, where K is a constant. In this process the temperataure of the gas is increased by ΔT. The amount of heat absorbed by gas is (R is gas constant).
View SolutionFor a monoatomic ideal gas undergoing an adiabatic change, the relation between temperature and volume TVx = constant, where x is
View SolutionA gas undergoes a process in which its pressure P and volume V are related as VP = constant. The bulk modulus of gas for this process
View SolutionAn ideal gas may expands from V0 to 2V0 according to following three processes. Molar specific heat for processes b will be

View SolutionThe molar heat capacity for the process shown in fig. is

View SolutionWhat is specific heat of a gas is an adiabatic process?
View SolutionA monatomic ideal gas is heated at constant volume until its pressure is doubled. It is again heated at constant pressure, until its volume is doubled. Find molar specific heat for the whole process.
View Solution
