A body of length 1m having cross sectional area 0.75m2 has heat flow through it at the rate of 6000Joule/sec. Then find the temperature difference if K=200Jm−1K−1.
20∘C
40∘C
80∘C
100∘C
The correct Answer is:B
To solve the problem, we will use the formula for the rate of heat flow through a material, which is given by:
dqdt=K⋅AL⋅ΔT
Where:
- dqdt = rate of heat flow (in Joules per second)
- K = thermal conductivity (in J/(m·K))
- A = cross-sectional area (in m²)
- L = length of the body (in m)
- ΔT = temperature difference (in K or °C)
Step 1: Identify the given values
From the problem, we have:
- dqdt=6000J/s
- K=200J/(m⋅K)
- A=0.75m2
- L=1m
Step 2: Rearrange the formula to solve for ΔT
We can rearrange the formula to isolate ΔT:
ΔT=dqdt⋅LK⋅A
Step 3: Substitute the known values into the equation
Now we substitute the known values into the rearranged formula:
ΔT=6000J/s⋅1m200J/(m⋅K)⋅0.75m2
Step 4: Calculate the denominator
First, calculate the denominator:
200⋅0.75=150J/K
Step 5: Calculate ΔT
Now substitute back into the equation:
ΔT=6000150=40K
Conclusion
The temperature difference ΔT is 40K (or 40°C since the size of the temperature difference is the same in Kelvin and Celsius).
Final Answer
ΔT=40°C
---
- dqdt = rate of heat flow (in Joules per second)
- K = thermal conductivity (in J/(m·K))
- A = cross-sectional area (in m²)
- L = length of the body (in m)
- ΔT = temperature difference (in K or °C)
From the problem, we have:
- dqdt=6000J/s
- K=200J/(m⋅K)
- A=0.75m2
- L=1m
We can rearrange the formula to isolate ΔT:
Now we substitute the known values into the rearranged formula:
First, calculate the denominator:
Now substitute back into the equation:
The temperature difference ΔT is 40K (or 40°C since the size of the temperature difference is the same in Kelvin and Celsius).
ΔT=40°C
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assignment (Section-B) Objective Type questions (one option is correct)
15 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assignment (Section-C) Objective Type questions (More than one option are correct)
12 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Try Youself
16 Videos
- TEST2BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST2EXERCISE - EXERCISE
2 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - ASSIGNMENT (SECTION -D) (Assertion - Reason Type Questions)
10 Videos
Similar Questions
Find the thermal resistance of an aluminium rod of length 20cm and area of cross section 1cm2 . The heat current is along the length of the rod. Thermal conductivity of aluminium =200Wm−1K−1 .
View Solution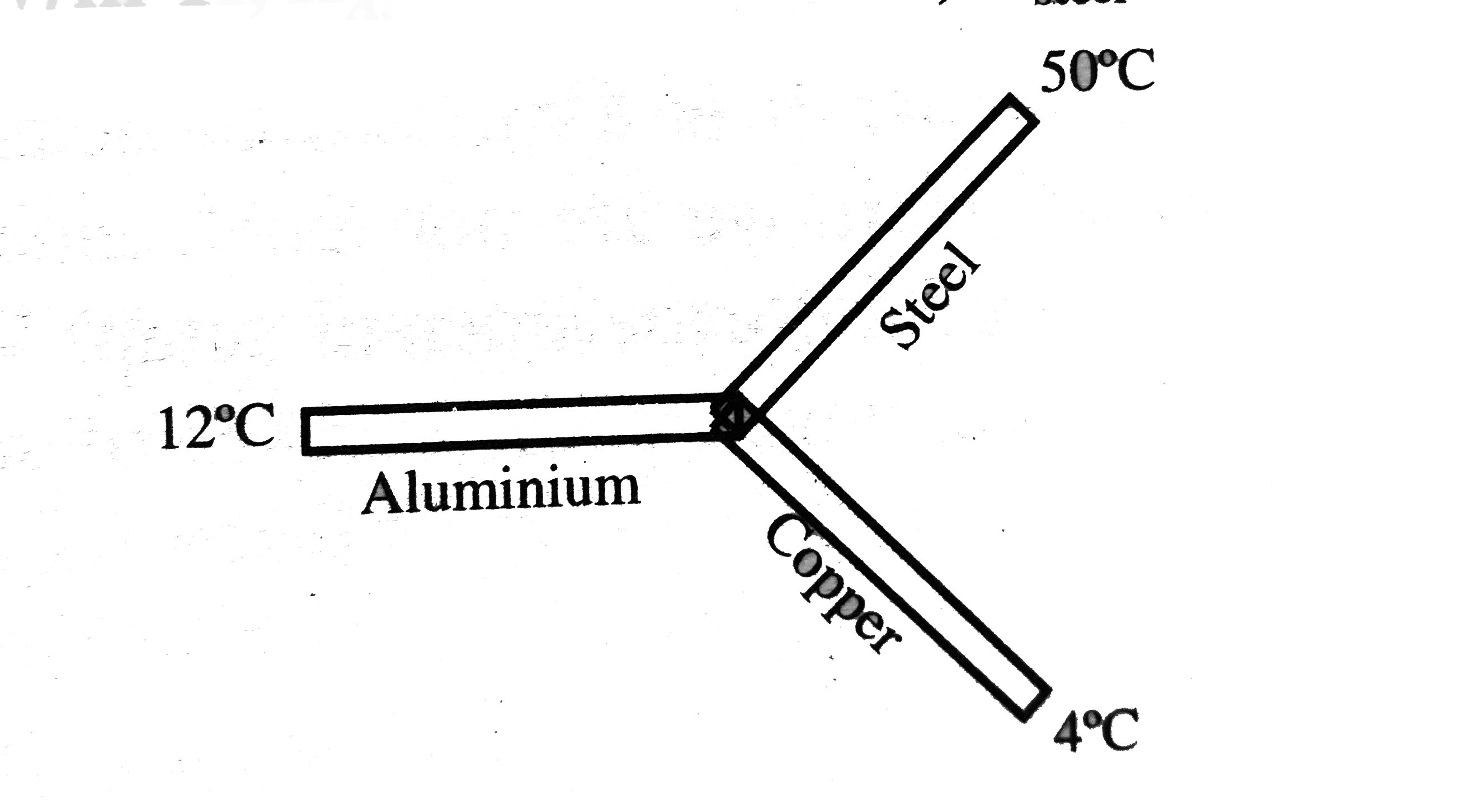
Three identical rods of length 1 m each, having cross-sectional area of 1cm2 each and made of aluminium, copper and steel, respectively, are maintained at temperatures of 12∘C,4∘C and 50∘C, respectively, at their separate ends. Find the teperature of their common junction.
[KCu=400W/m−K,KAl=200W/m−K,Ksteel=50W/m−K]
View Solution
Knowledge Check
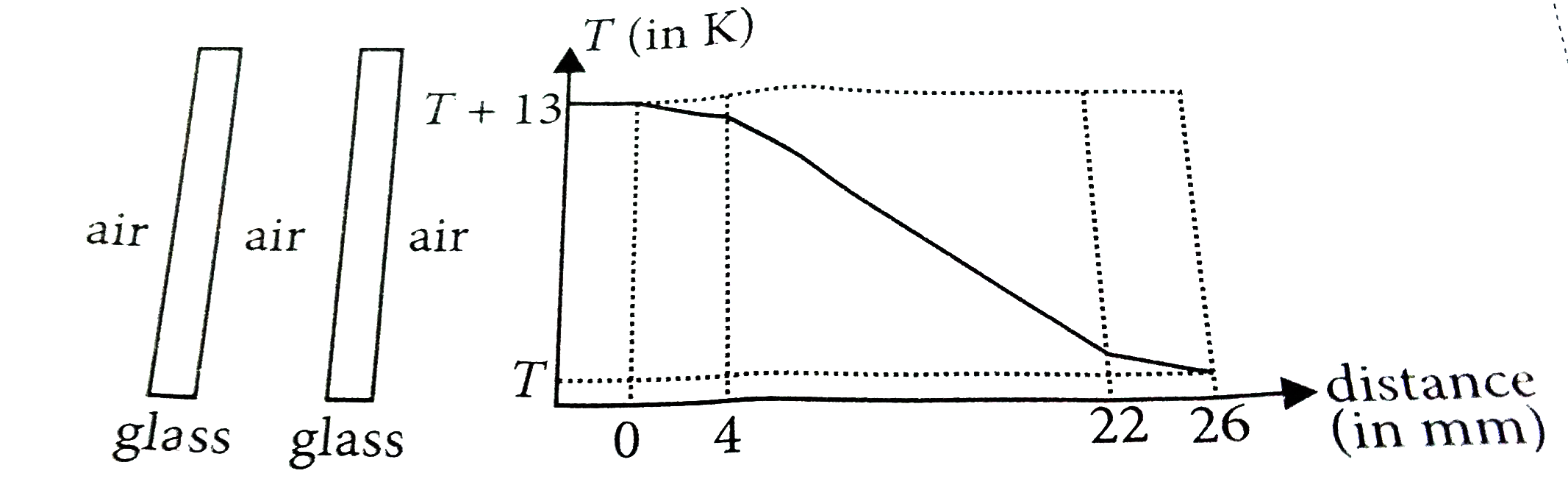
The figure show a cross-section of a double glass unit of a window on a vertical wall. A graph wall. A graph of the temperature at different points within the unit is show next to it. The temperature difference across the unit is 13K. It has a crossp-sectional area of 1.3m2 and the rate of heat flow through it is 65W. Then the correct statement is (Glass has a thermal conductivity of 1Wm−1K−1)
 AThe unit is in steady state and in thermal equilibriumBThe unit is in steady state but not in thermal equalibrium.CThe unit is not in steady state but is in thermalDThe unit neither in steady state nor in thermal equilibrium
AThe unit is in steady state and in thermal equilibriumBThe unit is in steady state but not in thermal equalibrium.CThe unit is not in steady state but is in thermalDThe unit neither in steady state nor in thermal equilibrium

Three identical rods of length 1 m each, having cross-sectional area of 1cm2 each and made of aluminium, copper and steel, respectively, are maintained at temperatures of 12∘C,4∘C and 50∘C, respectively, at their separate ends. Find the teperature of their common junction.
[KCu=400W/m−K,KAl=200W/m−K,Ksteel=50W/m−K]
View SolutionThe temperature difference between the ends of a rod of aluminium of length 1.0 m and area of cross section 5.0 cm2 is 200∘C. How much heat will flow through the rod in 5 minutes ? The coefficient of thermal conductivity of aluminium is 0.2 kJ s−1 m−1 ∘C−1.
View SolutionThe ends of a copper rod of length 1m and area of cross-section 1cm2 are maintained at 0∘C and 100∘C. At the centre of the rod there is a source of heat of power 25 W. Calculate the temperature gradient in the two halves of the rod in steady state. Thermal conductivity of copper is 400Wm−1K−1.
View SolutionThe ends of a copper rod of length 1m and area of cross-section 1cm2 are maintained at 0∘C and 100∘C. At the centre of the rod there is a source of heat of power 25 W. Calculate the temperature gradient in the two halves of the rod in steady state. Thermal conductivity of copper is 400Wm−1K−1.
View SolutionThe water flowing through the same tube having two different cross section areas has different flow rates .
View SolutionA rod of length l and cross sectional area A has a variable conductivity given by K=αT, where α is a positive constant T is temperatures in Kelvin. Two ends of the rod are maintained at temperatures T1 and T2(T1>T2). Heat current flowing through the rod will be
View SolutionA steel frame (K=45Wm−1C−1) of total length 60cm and cross sectional area 0.2cm2 , Forms three side of a square. The free ends are maintained at 20∘C and 40∘C . Find the rate of heat flow through a cross section of the frame.
View Solution
