According to ‘Newton’s Law of cooling’, the rate of cooling of a body is proportional to the
Temperature of the body
Temperature of the surrounding
Fourth power of the temperature of the body
Difference of the temperature of the body and the surroudings
The correct Answer is:D
To solve the question regarding Newton's Law of Cooling, we can follow these steps:
Step 1: Understand Newton's Law of Cooling
Newton's Law of Cooling states that the rate of change of temperature of a body is proportional to the difference between its own temperature and the temperature of its surroundings.
Step 2: Define the Variables
Let:
- T2 = Initial temperature of the body
- T1 = Final temperature of the body after time T
- Tθ = Temperature of the surroundings
Step 3: Establish the Rate of Cooling
According to the law, the rate of cooling can be expressed mathematically as:
dTdt∝(T−Tθ)
where T is the temperature of the body at any time t.
Step 4: Express the Mean Temperature Difference
The mean temperature difference can be expressed as:
Mean Temperature Difference=(T2+T1)2−Tθ
Step 5: Identify the Proportionality
From the above, we can conclude that the rate of cooling is proportional to the temperature difference between the body and the surroundings:
Rate of Cooling∝(T−Tθ)
Step 6: Conclusion
Thus, according to Newton's Law of Cooling, the rate of cooling of a body is proportional to the difference between the temperature of the body and the temperature of the surroundings.
Final Answer
The correct statement is that the rate of cooling of a body is proportional to the difference between the temperature of the body and the surrounding temperature.
---
Newton's Law of Cooling states that the rate of change of temperature of a body is proportional to the difference between its own temperature and the temperature of its surroundings.
Let:
- T2 = Initial temperature of the body
- T1 = Final temperature of the body after time T
- Tθ = Temperature of the surroundings
According to the law, the rate of cooling can be expressed mathematically as:
dTdt∝(T−Tθ)
where T is the temperature of the body at any time t.
The mean temperature difference can be expressed as:
Mean Temperature Difference=(T2+T1)2−Tθ
From the above, we can conclude that the rate of cooling is proportional to the temperature difference between the body and the surroundings:
Rate of Cooling∝(T−Tθ)
Thus, according to Newton's Law of Cooling, the rate of cooling of a body is proportional to the difference between the temperature of the body and the temperature of the surroundings.
The correct statement is that the rate of cooling of a body is proportional to the difference between the temperature of the body and the surrounding temperature.
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assignment (Section-B) Objective Type questions (one option is correct)
15 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assignment (Section-C) Objective Type questions (More than one option are correct)
12 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Try Youself
16 Videos
- TEST2BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST2EXERCISE - EXERCISE
2 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - ASSIGNMENT (SECTION -D) (Assertion - Reason Type Questions)
10 Videos
Similar Questions
Knowledge Check
Assertion: According to Newton's law of cooling, the rate of loss of heat, −dQ/dt of the body is directly proportional to the difference of temperature.
Reason :This law holds for all type of temperature differences.Alaw of thermometryBNewton's law of coolingClaw of calorimetryDzeroth lawAssertion: According to Newton's law of cooling, the rate of loss of heat, −dQ/dt of the body is directly proportional to the difference of temperature.
Reason :This law holds for all type of temperature differences. a) If both assertion and reason are true and reason is the correct explanation of assertion. b) If both assertion and reason are true and reason is not the correct explanation of assertion. c) If assertion is true and reason is false. d) If both assertion and reason are false.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true and reason is not the correct explanation of assertion.CIf assertion is true and reason is false.DIf both assertion and reason are false.A hot liquid is kept in a bog room. Accoding to Newton's law of cooling rate of cooling liquid (represented as y) is plotted against its temperature T. Which of the following curves may represent the plot?
A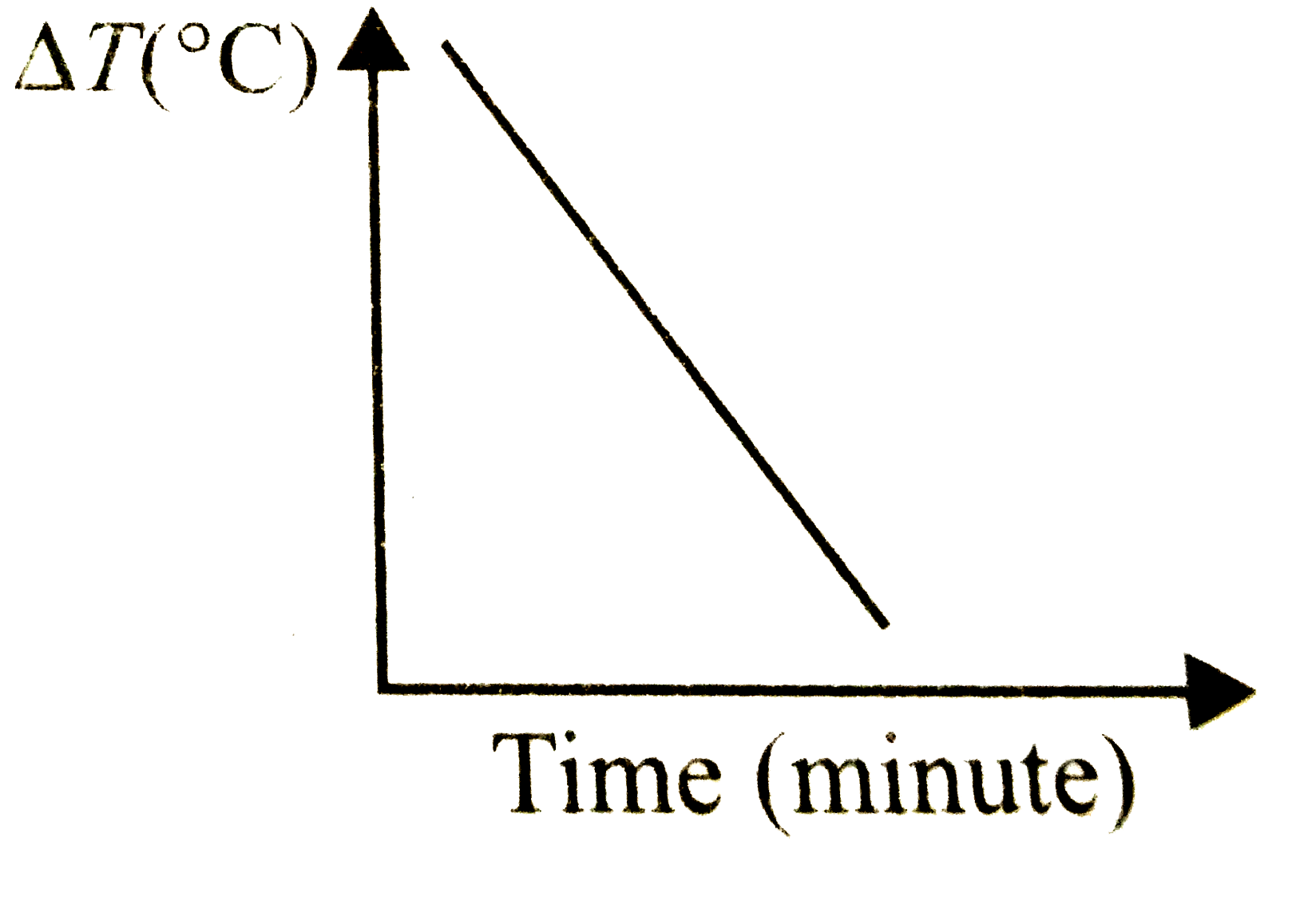 B
B C
C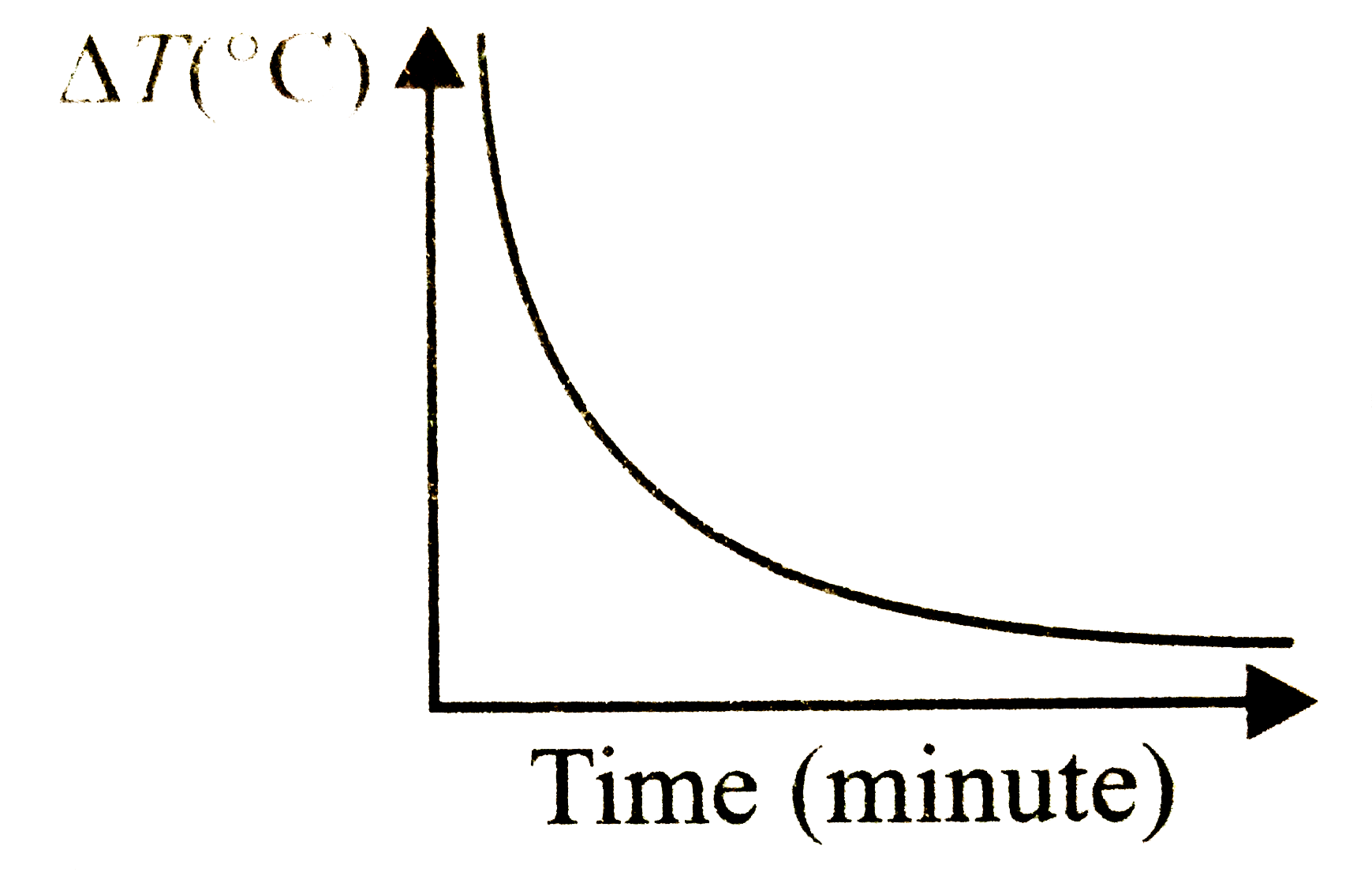 D
D
According to Newton's law, rate of cooling is proportional to the difference between the temperature of the body and the temperature of the air. If the temperature of the air is 20∘C and body cools for 20 min from 100∘C to 60∘C then the time it will take for it temperature to drop to 30∘ is
View SolutionDerive Newton's law of cooling to show that the rate of loss of heat from the body is proportional to the temperature difference between the body and its surroundings.
View SolutionA hot liquid is kept in a big room. According to Newton's law of cooling rate of cooling liquid (represented as y) is plotted against its temperature T. Which of the following curves may represent the plot?
View SolutionA hot body placed in air is cooled down according to Newton's law of cooling, the rate of decrease of temperature being k times the temperature difference from the surrounding. Starting from t=0 , find the time in which the body will loss half the maximum heat it can lose.
View SolutionA hot body placed in air is cooled down according to Newton's law of cooling, the rate of decrease of temperature being k times the temperature difference from the surrounding. Starting from t=0 , find the time in which the body will lose half the maximum heat it can lose.
View Solution
