Let →Mand→L represent magnetic moment and angular momentum vectors for the electron in the above example. What is the sign of the dot product, →M.→L. (positive, negative or zero) ?
The correct Answer is:Negative
To determine the sign of the dot product →M⋅→L for the electron's magnetic moment →M and angular momentum →L, we can follow these steps:
Step 1: Understand the Definitions
- The magnetic moment →M for a revolving electron can be defined in terms of the current I and the area A it sweeps out:
→M=I⋅A
- The angular momentum →L of the electron is given by:
→L=→r×→p=→r×(m→v)
Step 2: Calculate the Current I
- The current I due to the electron moving in a circular path is given by:
I=QT
where Q is the charge of the electron (which is negative, −e) and T is the time period of one complete revolution.
Step 3: Determine the Time Period T
- The time period T for the electron moving in a circular path of radius r with velocity v is:
T=2πrv
Step 4: Substitute I into the Magnetic Moment Equation
- Substituting I into the magnetic moment equation:
→M=I⋅A=(−eT)⋅πr2
After substituting T:
→M=(−ev2πr)⋅πr2=−evr2
Step 5: Express Angular Momentum
- The angular momentum can be expressed as:
→L=m→v⋅r
Step 6: Calculate the Dot Product →M⋅→L
- The dot product →M⋅→L is:
→M⋅→L=(−e2m→v⋅r)⋅(m→v⋅r)
Since →M and →L are in opposite directions, the dot product yields a negative value:
→M⋅→L<0
Conclusion
The sign of the dot product →M⋅→L is negative. This indicates that the magnetic moment and angular momentum vectors are in opposite directions.
- The magnetic moment →M for a revolving electron can be defined in terms of the current I and the area A it sweeps out:
→M=I⋅A
- The angular momentum →L of the electron is given by:
→L=→r×→p=→r×(m→v)
- The current I due to the electron moving in a circular path is given by:
I=QT
where Q is the charge of the electron (which is negative, −e) and T is the time period of one complete revolution.
- The time period T for the electron moving in a circular path of radius r with velocity v is:
T=2πrv
- Substituting I into the magnetic moment equation:
→M=I⋅A=(−eT)⋅πr2
After substituting T:
→M=(−ev2πr)⋅πr2=−evr2
- The angular momentum can be expressed as:
→L=m→v⋅r
- The dot product →M⋅→L is:
→M⋅→L=(−e2m→v⋅r)⋅(m→v⋅r)
Since →M and →L are in opposite directions, the dot product yields a negative value:
→M⋅→L<0
The sign of the dot product →M⋅→L is negative. This indicates that the magnetic moment and angular momentum vectors are in opposite directions.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Assignment (Section A) Objective Type Questions (One option is correct)
55 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Assignment (Section B) Objective Type Questions (One option is correct)
35 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Illustration
14 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D
16 Videos
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
Similar Questions
Knowledge Check
If→a is a non-zero vector and m is a non-zero scalar, then m →a is a unit vector if
Am=±1Bm=|a|Cm=±|→a|Dm=±1|→a|
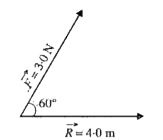
The vector →F is a force of 3.0 newton making an angle of 60∘ with the displacement . →R of magnitude 4.0 m , find
the value of the dot product →F.→R
View SolutionIf →j and →E are current density and electric field inside a current carrying conductor at an instant then →j.→E is
(1) Positive (2) Negative
(3) Zero (4) May be positive or negative
View SolutionThe sum of three vectors shown in figure, is zero.
(i) What is the magnitude of vector −−→OB ?
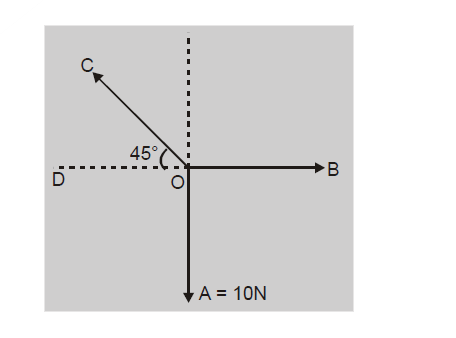
(ii) What is the magnitude of vector −−→OC ?
View SolutionDerive an expression for the magnetic moment (→μ) of an electron revolving around the nucleus in termsof its angular momentum (→l). What is the direction of the magnetic moment of the electron with respect to its angular momentum?
View SolutionWrite a vector normal to the plane →r=l→b+m→c
View SolutionIf |→a|=∣∣→b∣∣, then (→a+→b).→a−→b= a. positive b. negative c. 0 d. none of these
View SolutionLet vector →V=(2,3) and vector →U=(6,−4).
(i) What is the resultant of →Uand→V?
View Solution
